1

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny systemu dyskretnego

System  dyskretny

 to  system,  w  którym  zbiór 

rozpatrywanych  wartości  argumentu  t  jest  dyskretny  i 

chociażby część współrzędnych, albo też oddziaływań, jest 

ciągiem impulsów.

Systemy dyskretne

Systemy ciągło-dyskretne

Systemy dyskretne

  tylko  urządzenia  dyskretne 

np. komputery, filtry cyfrowe

  elementy  ciągłe  i  dyskretne 

np.  układ  ciągły  z  regulatorem 

cyfrowym

2

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny systemu dyskretnego

t

x(t)

t

1

x(t

1

)

t

x(t)

k

x(k)

k+1

k-1

T

model ciągły

model dyskretny (impulsowy)

T – czas próbkowania

Proces  przekształcenia  sygnału  ciągłego  w  dyskretny  nazywamy 

kwantowaniem

.

3

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny systemu dyskretnego

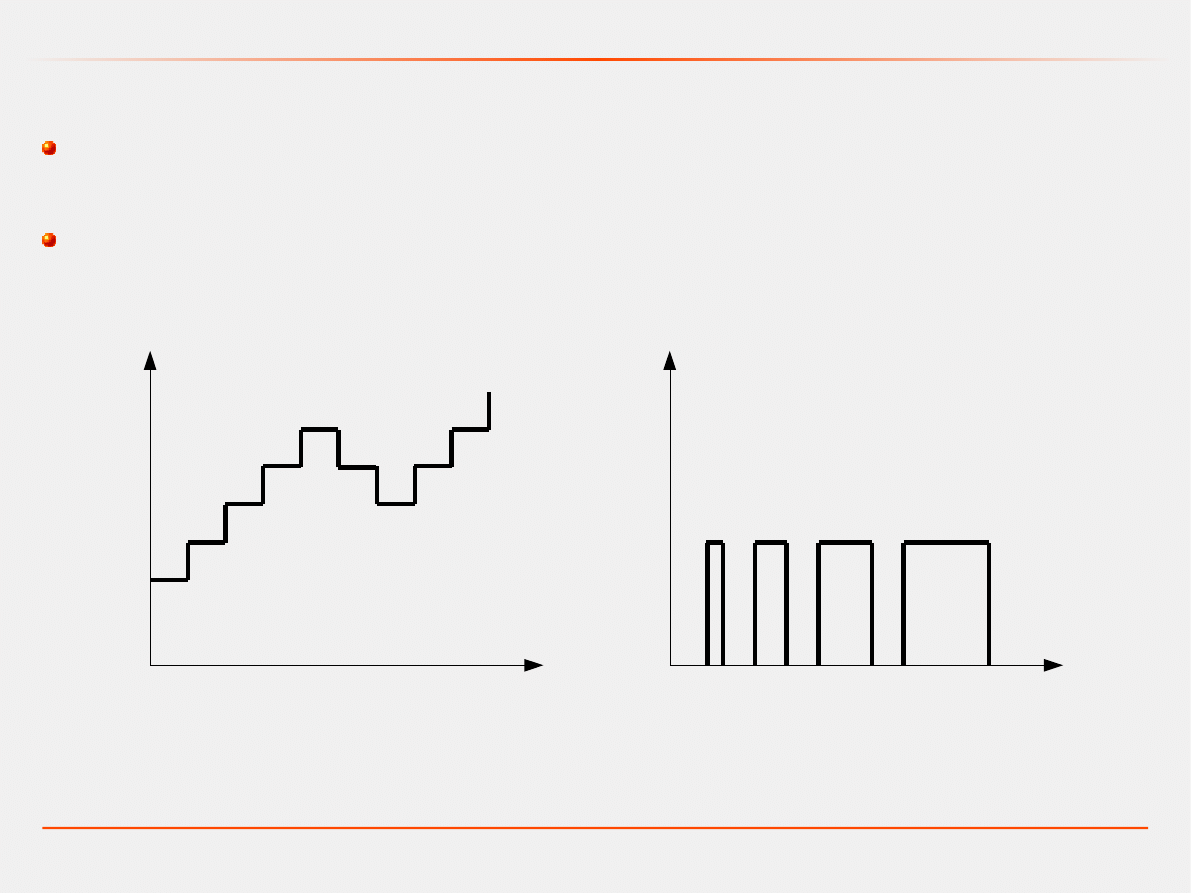
model  kwantowy

 -  zmienne  modelu  przyjmują  tylko  określone 

wartości,

model  skończony

 -  zmienne  modelu  przyjmują  tylko  skończoną 

liczbę wartości,

t

x(t)

model kwantowy

t

x(t)

model skończony

4

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny systemu dyskretnego

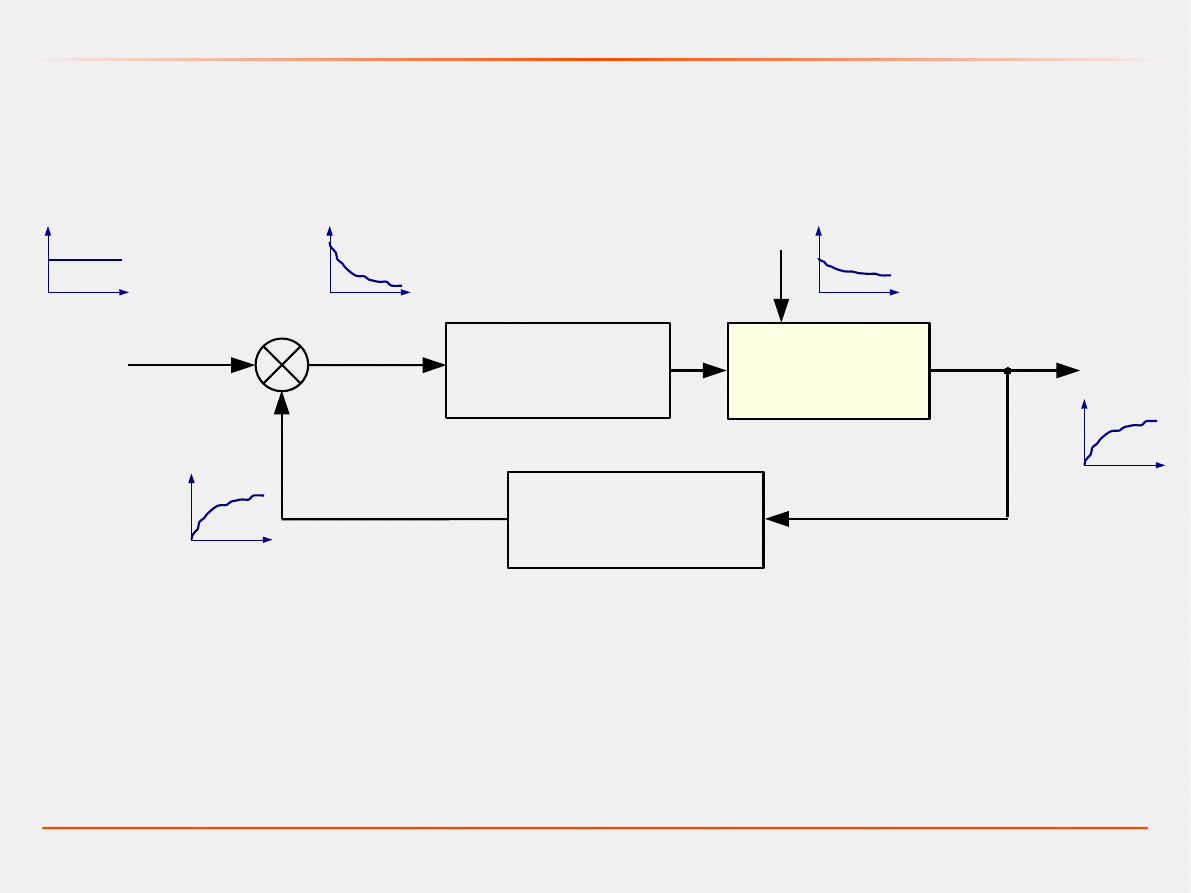
Przykład:  Sterowanie  prędkością  obrotową  silnika  elektrycznego  – 
układ ciągły

WZMACNIACZ

TACHOMETR

+

-

SILNIK

prędkość

napięcie

napięcie
zadające

Z

y*(t)

prędkość wału

pomierzona
prędkość wału

e(t)

y

0

(t)

y*

t

y

t

y(t)

e

t

y

0

t

z

t

Tachometr  –  prądnica,  której  wał  połączony  jest  z  wałem  silnika, 

napięcie tej prądnicy jest proporcjonalne do prędkości obrotowej

5

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny systemu dyskretnego

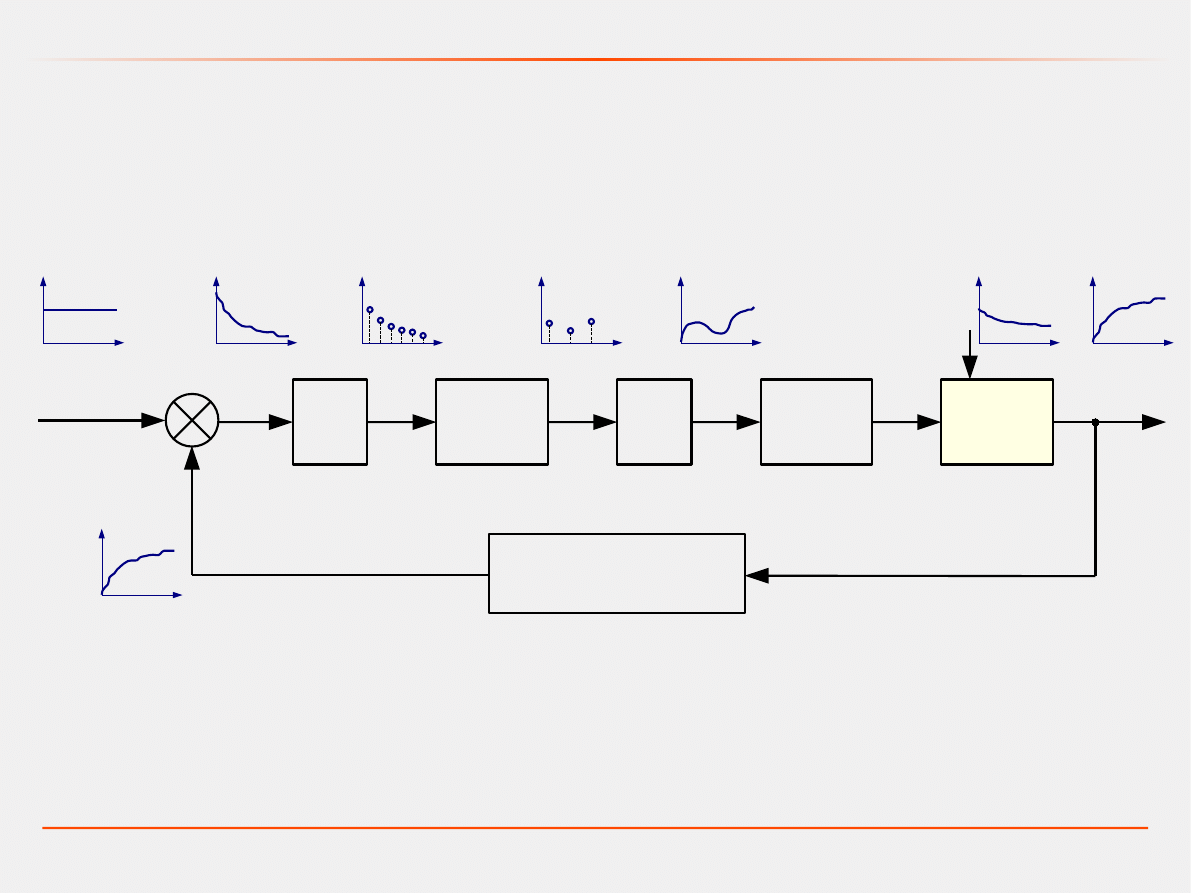
Przykład:  Sterowanie  prędkością  obrotową  silnika  elektrycznego  – 
układ ciągły-dyskretny

TACHOMETR

+

-

prędkość

napięcie

napięcie

Z

y*(t)

prędkość wału

pomierzona
prędkość wału

e(t)

y

0

(t)

y*

t

y

t

y(t)

e

t

y

0

t

z

t

A / D

Komputer

D / A

Wzmacniacz

SILNIK

f(t)

p(t)

r(t)

f

t

p

t

r

t

6

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny systemu dyskretnego

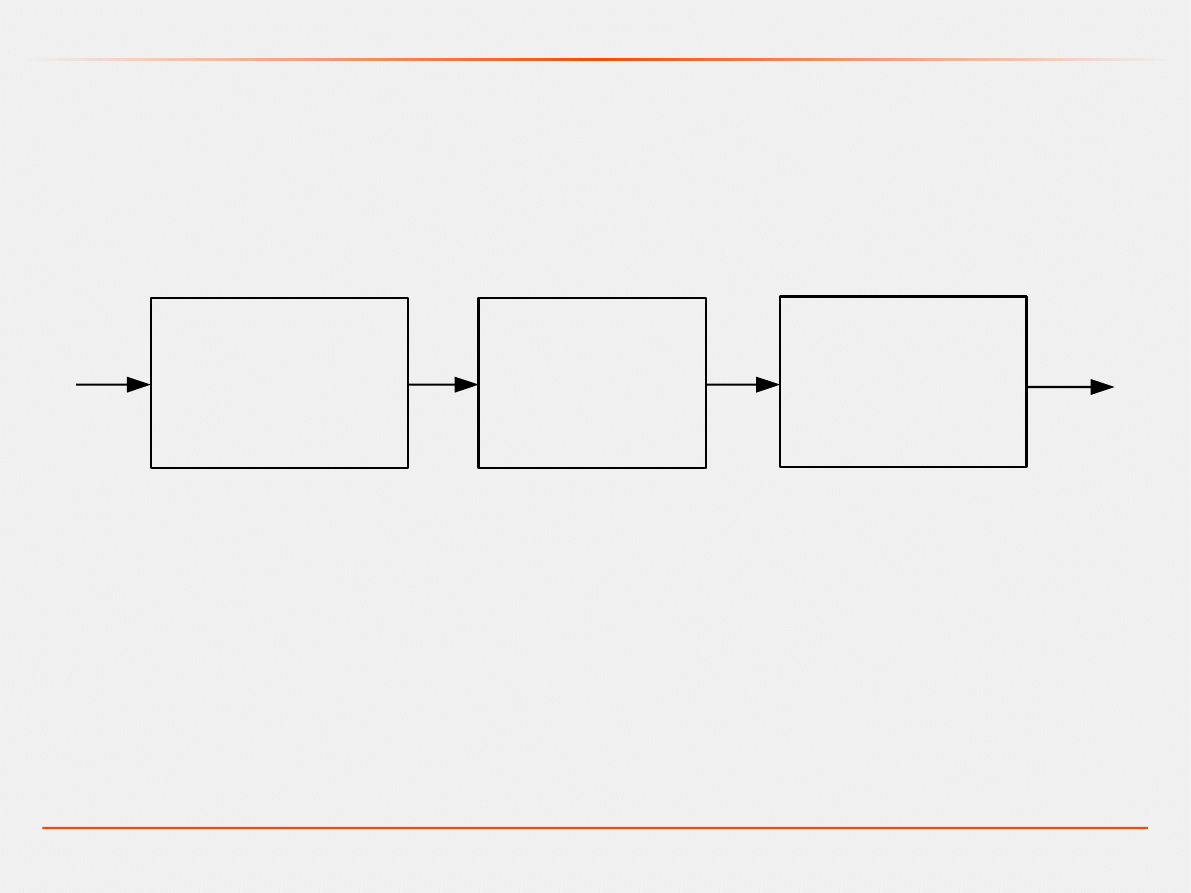
Konwersja sygnałów

e(t)

●

 Opóźnienie konwersji

●

 Błąd kwantyzacji

f(t)

●

 Czas obliczeń

●

 Błąd kwantyzacji

p(t)

●

Opóźnienie konwersji

●

 Błąd aproksymacji

r(t)

A/D

KOMPUTER

D/A

Czas  próbkowania  nie  może  być  krótszy  od  sumy  czasu  konwersji 

przetwornika A/D i czasu obliczeń komputera.

7

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

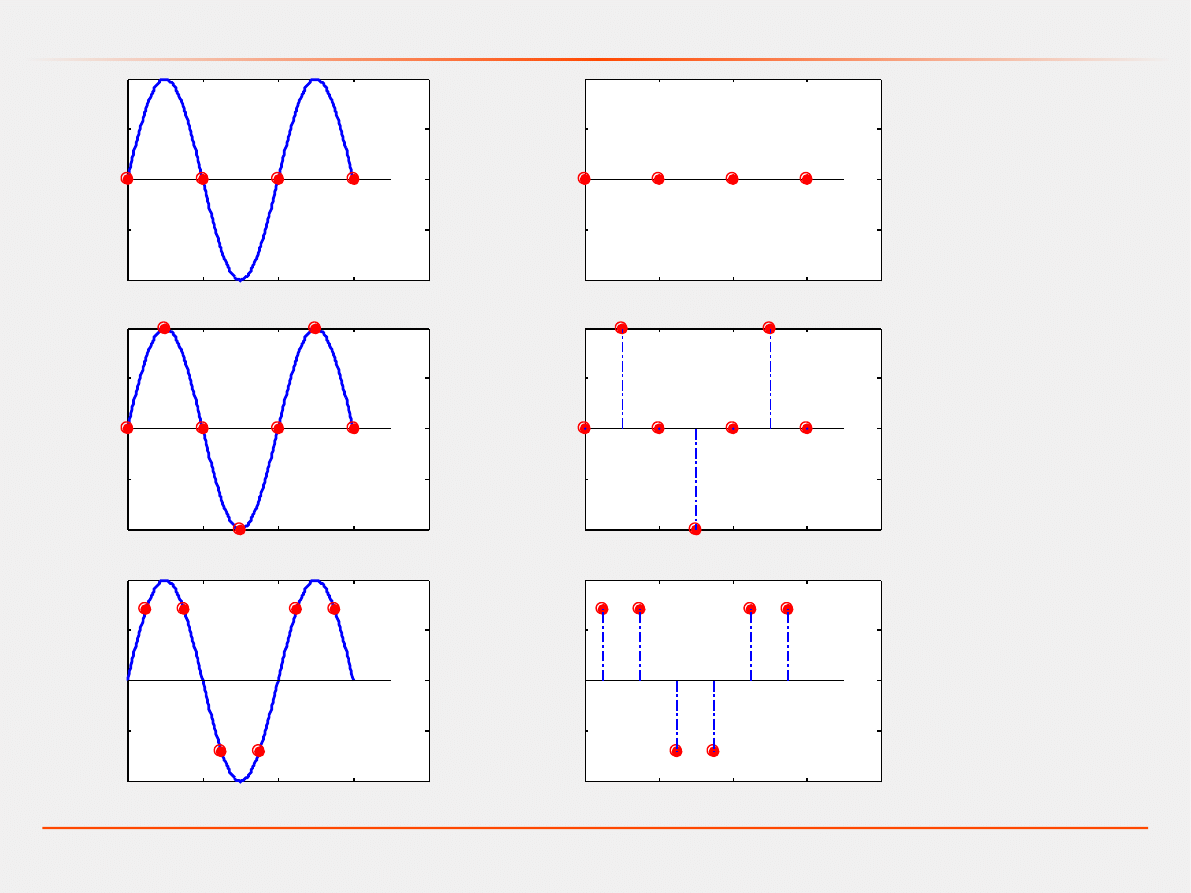
Dobór czasu próbkowania

0

1

2

3

4

-1

-0.5

0

0.5

1

f(

t)

t

0

1

2

3

4

-1

-0.5

0

0.5

1

f(

t)

t

0

1

2

3

4

-1

-0.5

0

0.5

1

f(

t)

t

0

1

2

3

4

-1

-0.5

0

0.5

1

f

*

(t

)

t

0

1

2

3

4

-1

-0.5

0

0.5

1

f

*

(t

)

t

0

1

2

3

4

-1

-0.5

0

0.5

1

f

*

(t

)

t

T=1

T=0.5

T=0.5

8

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny systemu dyskretnego

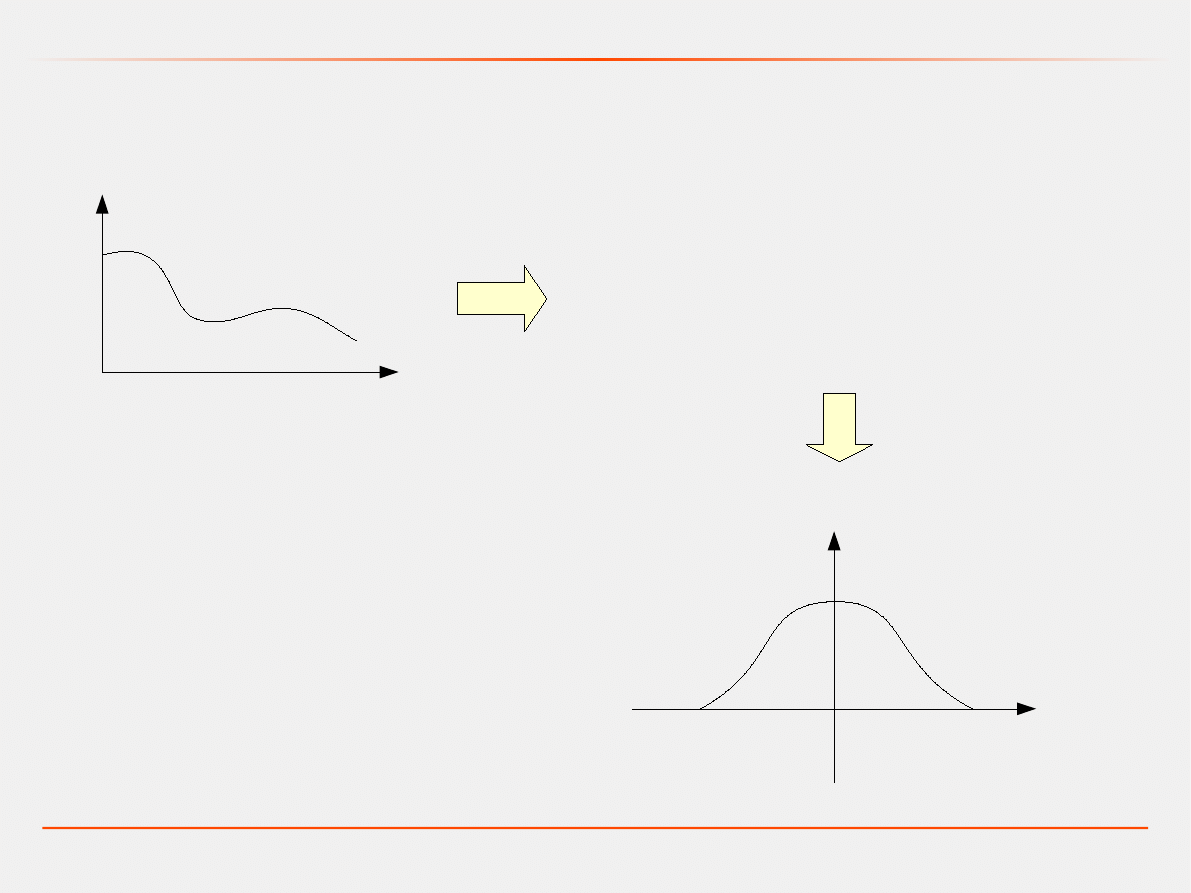
Twierdzenie Shannona-Kotielnikowa 

t

f(t)

sygnał ciągły

ω

|F(jω)|

-ω

c

ω

c

Przekształcenie Fouriera

F  j =

∫

−∞

∞

xt ⋅e

−

j  t

dt

9

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny systemu dyskretnego

Twierdzenie Shannona-Kotielnikowa 

Do  tego,  aby  sygnał  ciągły  o  widmie  ograniczonym 
maksymalną  częstotliwością 

ω

c

 można  było  odtworzyć 

dokładnie,  według  jego  wartości  dyskretnych,  konieczne 
jest aby częstotliwość kwantowania 

ω

0

 spełniała warunek:



0



2⋅

c

Okres kwantowania T

0

 powinien spełniać warunek:

T

0







c

10

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny systemu dyskretnego

{

x[k1]= f  x [k ] , u[k ] , k 

y[ k ]=g  x[k ] , u[k ] , k 

Opis  dyskretnego  równania  nieliniowego  w  przestrzeni 

stanów

{

X [k1]= A[ k ] X [ k ]B [k ]U [k ]

Y [k ]=C [k ] X [k ]D[ k ]U [ k ]

Opis dyskretnego równania liniowego w przestrzeni stanów

Równania  różnicowe

 określają  stan  systemu  w  chwili 

[k+1]  w  zależności  od  stanu  z  chwili  poprzedniej  [k]  i 

wartości wymuszenia u[k].

11

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny systemu dyskretnego

Metody  przekształcania  równań  różniczkowych  (ciągłych) 

na równania różnicowe (dyskretne)

dx t 

dt

=

x[ kT T ]−x[kT ]

T

metoda 

różnicowa 

Eulera 

w 

przód 

(algorytm 

ekstrapolacyjny)

dx t 

dt

=

x[ kT ]−x[kT −T ]

T

metoda 

różnicowa 

Eulera 

wstecz 

(algorytm 

interpolacyjny)

12

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

B

A

Model dynamiczny systemu dyskretnego

Przykład. Dyskretyzacja modelu ciągłego.

˙X t =



0

1

−

2 −2



⋅

X t 



0
2



⋅

U t 

˙X t =A⋅X tB⋅U t 

X [ kT T ]= I  A⋅T ⋅X [ kT ]B⋅T⋅U [kT ]

X [ k 1]=



1

T

−

2T 1−2T



⋅

X [ k ]



0

2T



⋅

U [ k ]

13

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Przekształcenie Laplace'a

Istnieje również przekształcenie odwrotne:

F  z =Z

{

f [ k ]

}

=

∑

k =0

∞

F k  z

−

k

Przekształcenie Laurenta

 (przekształcenie Z) przyporządkowuje 

danej dyskretnej funkcji czasu f[k] funkcję zmiennej zespolonej z, 

F(z), którą nazywamy transformatą Z (Laurenta)

f [k ]=Z

−

1

{

F  z 

}

14

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Przekształcenie Laplace'a

Przekształcenie Laurenta

 umożliwia sprowadzenie układu równań 

różnicowych  reprezentujących  model  dyskretny  liniowy  i 

stacjonarny do układu równań algebraicznych.

{

X [k1]= A[ k ] X [ k ]B [k ]U [k ]

Y [k ]=C [k ] X [k ]D[ k ]U [ k ]

{

z⋅X  z−zX 0= AX  zBU  z

Y  z=CX  zDU  z

{

X  z= zI −A

−

1

zX 0 zI −A

−

1

BU  z

Y  z=CX  zDU  z

15

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

Model dynamiczny – transmitancja operatorowa

G  z=

Y  z 

U  z 

=

C  zI −A

−

1

BD

Transmitancja  operatorowa  G(z)

 

jest  zdefiniowana  jako 

stosunek  transformaty  Z  sygnału  wyjściowego  Y(z)  do 

transformaty  Z  sygnału  wejściowego  U(z),  przy  założeniu, 
że wszystkie warunki początkowe są zerowe.

16

MODELOWANIE I SYMULACJA

Szczecin - 5.01.2009

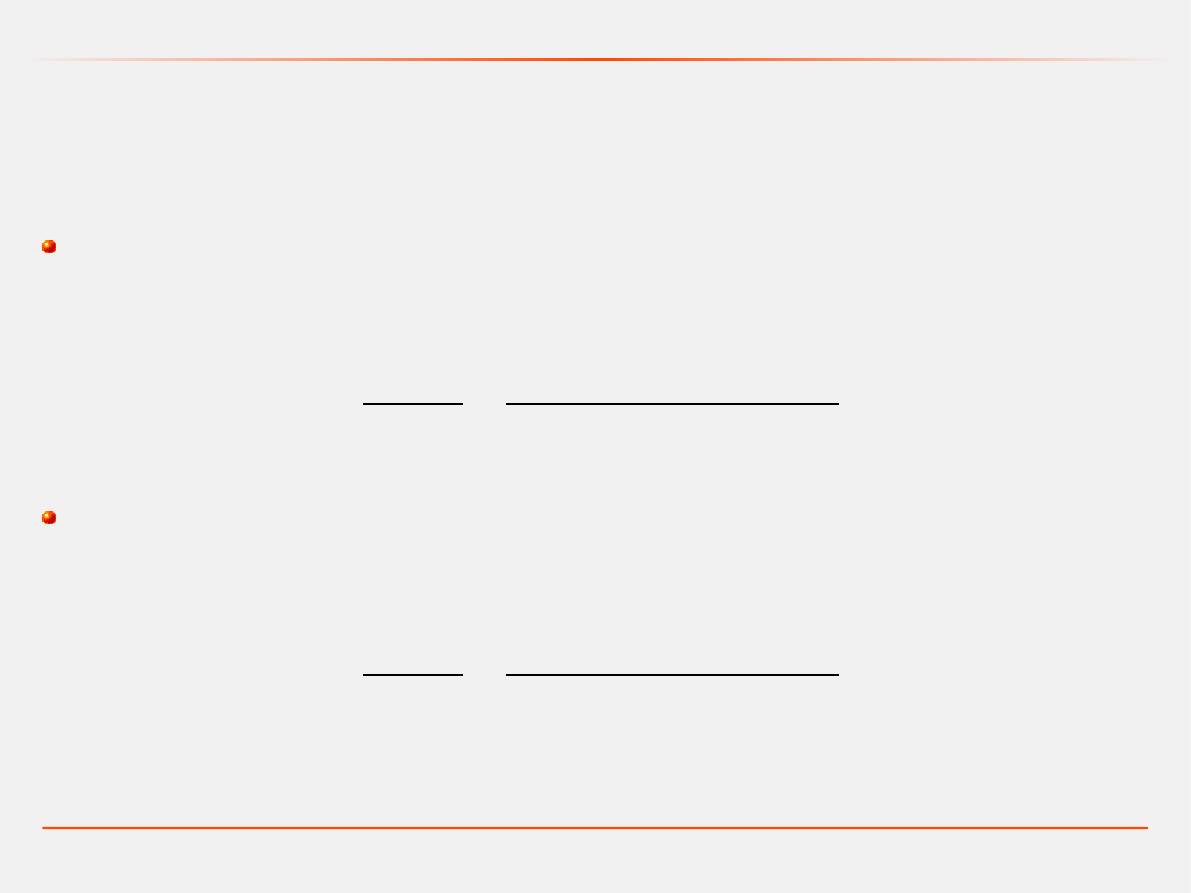
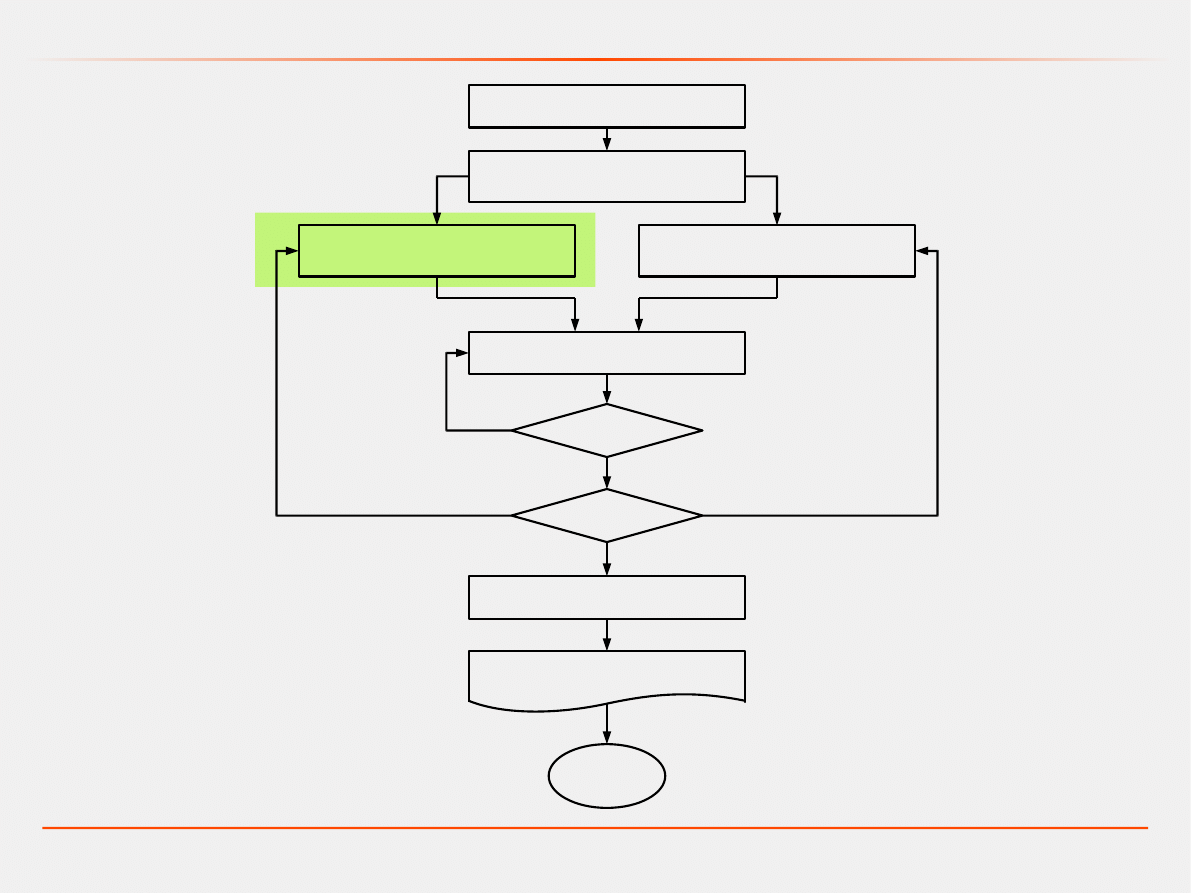
Sformułowanie problemu

Ustalenie celów

 i planu działania

Zbieranie danych

Tworzenie modelu 

konceptualnego

Kodowanie modelu

Testowanie

Nie

Wdrożenie

Tworzenie dokumentacji

 i raportów

Weryfikacja

Walidacja

Nie

Nie

 Tak

 Tak

Proces modelowania