Metody probabilistyczne i statystyka
17. WERYFIKACJA HIPOTEZ STATYSTYCZNYCH
Weryfikacja (testowanie) hipotez statystycznych
to drugi, obok
estymacji, podstawowy rodzaj wnioskowania statystycznego.
Hipoteza statystyczna
to każde przypuszczenie dotyczące
wielkości parametru rozkładu zmiennej losowej w populacji generalnej
lub próbnej, albo też postaci tego rozkładu, uzyskane na podstawie
próby losowej.
Dwie grupy hipotez statystycznych:
•
parametryczne
, związane z wartościami parametrów,
•
nieparametryczne
, związane z postacią rozkładów.
Wykład 5-6/ 1
StatGraph.lnk
Metody probabilistyczne i statystyka
Testy parametryczne
Θ
- parametr populacji generalnej
T - przypuszczalna (hipotetyczna) wartość parametru populacji
generalnej
H
0
- hipoteza zerowa o postaci:
H
0
:
Θ
= T
co czyta się:
"Stawiamy hipotezę zerową głoszącą, że wartość parametru
Θ
jest równa T"
lub
"Stawiamy hipotezę zerową głoszącą, że różnica pomiędzy
parametrem
Θ
a jego oceną T jest statystycznie nieistotna (jest
na poziomie zerowym)" - stąd nazwa -
hipoteza zerowa
.
Wykład 5-6/ 2
StatGraph.lnk
Metody probabilistyczne i statystyka
H
1
- hipoteza alternatywna (dla każdej hipotezy zerowej określa się
hipotezę alternatywną) o postaciach:
H
1
:
Θ
≠ T
lub
H
1
:
Θ
> T
lub
H
1
:
Θ
< T
Dwie ostatnie postaci hipotezy alternatywnej określa się jako
hipotezy jednostronne.
Postawioną hipotezę zerową weryfikuje się za pomocą
odpowiedniego sprawdzianu zwanego też testem, który określa się jako
zmienną losową o postaci:
R
0
=
Θ
T
wyznaczającą różnicę, dla której następnie buduje się
obszar
krytyczny
odrzuceń hipotezy zerowej na podstawie wartości krytycznej
R
α
dla danego
poziomu istotności
α
.
Wykład 5-6/ 3
StatGraph.lnk
Metody probabilistyczne i statystyka
Każdą hipotezę zerową weryfikuje się z pewnym
prawdopodobieństwem pewności zwanym
poziomem ufności 1-
α
.
Odrzucenie hipotezy zerowej H
0
Jeżeli obliczona na podstawie próby wartość sprawdzianu (testu)
R
znajduje się w obszarze krytycznym odrzuceń, to hipotezę zerową
H
0
odrzuca się na korzyść hipotezy alternatywnej
H
1
. W przypadku
przeciwnym stwierdza się, że dla danego poziomu istotności
α
nie ma
podstaw do odrzucenia hipotezy zerowej
H
0
.
Wykład 5-6/ 4
StatGraph.lnk
Metody probabilistyczne i statystyka
Procedura postępowania dla zweryfikowania parametrycznej
hipotezy zerowej H
0
1.
określić hipotezę zerową
H
0
oraz jej alternatywę
H
1
2.
przyjąć poziom istotności
α
oraz liczebność próby
3. określić rozkład zbiorowości generalnej
4.
określić test dla weryfikacji hipotezy zerowej
H
0
5. obliczyć wartość testu na podstawie próby
6.
odczytać z tablic rozkładu danego testu wartość krytyczną
wyznaczającą obszar odrzuceń i przyjąć (lub odrzucić) hipotezę
zerową
H
0
Wykład 5-6/ 5
StatGraph.lnk
Metody probabilistyczne i statystyka
Testy dla wartości średniej populacji
Model I
Badana cecha w populacji generalnej ma rozkład normalny N(
µ
,
σ
),
przy czym
σ
jest znane. Na podstawie n-elementowej próby
zweryfikować hipotezę zerową:
H
0
:
µ
=
µ
0
gdzie
µ
0
jest konkretną, hipotetyczną wartością średniej, wobec
hipotezy alternatywnej (dwustronnej):
H
1
:
µ
≠
µ
0
Wykład 5-6/ 6
StatGraph.lnk
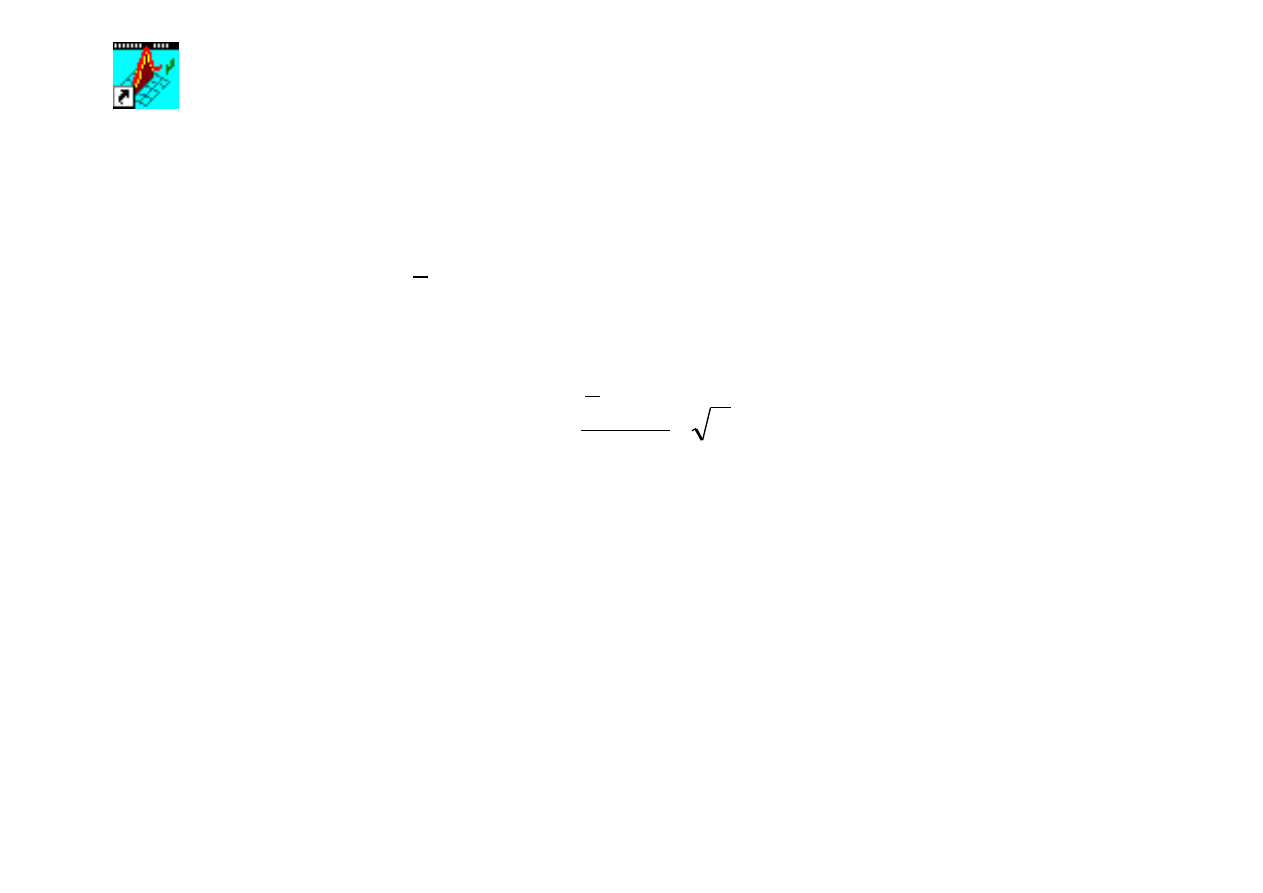
Metody probabilistyczne i statystyka
Test dla hipotezy zerowej jest następujący:
1. na podstawie wyników z próby oblicza się:
1.1.
wartość średnią
x
1.2.
wartość zmiennej standaryzowanej U wg wzoru:
n
x
u
⋅
−
=
σ
µ
0
2.
z tablic rozkładu normalnego standaryzowanego N(0,1), dla
założonego poziomu istotności
α
wyznacza się wartość krytyczną
u
α
/2
, taką by zachodziło:
P(|U|
≥
u
α
/2
) =
α
Wykład 5-6/ 7
StatGraph.lnk
Metody probabilistyczne i statystyka
Obszar krytyczny testu określony jest zależnością:
|U|
≥
u
α
/2
tzn. że gdy z próby otrzymamy taką wartość u, że zachodzi:
|u|
≥
u
α
/2
to hipotezę zerową H
0
odrzucamy. W przypadku przeciwnym, gdy
zachodzi:
|u|
<
u
α
/2
nie ma podstaw do odrzucenia H
0
.
Wykład 5-6/ 8
StatGraph.lnk
Metody probabilistyczne i statystyka
UWAGA:
Powyższy test jest testem z dwustronnym obszarem krytycznym i
stosuje się go tylko dla dwustronnej hipotezy alternatywnej:
H
1
:
µ
≠
µ
0
Przypadek 1
Hipoteza alternatywna H
1
ma postać:
H
1
:
µ
<
µ
0
W tym przypadku stosuje się test z lewostronnym obszarem
krytycznym, określonym nierównością:
U
≤
-u
α
Wykład 5-6/ 9
StatGraph.lnk
Metody probabilistyczne i statystyka
przy czym wartość u
α
wyznacz się z tablic rozkładu normalnego
standaryzowanego w taki sposób by była spełniona zależność:
P(U
≤
-u
α
) =
α
Hipotezę zerową odrzuca się, jeżeli wyznaczona z próby wartość
zmiennej u spełnia nierówność:
u
≤
-u
α
Przypadek 2
Hipoteza alternatywna H
1
ma postać:
H
1
:
µ
>
µ
0
Wykład 5-6/ 10
StatGraph.lnk
Metody probabilistyczne i statystyka
W tym przypadku stosuje się test z prawostronnym obszarem
krytycznym, określonym nierównością:
U
≥
u
α
przy czym wartość u
α
wyznacz się z tablic rozkładu normalnego
standaryzowanego w taki sposób by była spełniona zależność:
P(U
≥
u
α
) =
α
Hipotezę zerową odrzuca się, jeżeli wyznaczona z próby wartość
zmiennej u spełnia nierówność:
u
≥
u
α
Wykład 5-6/ 11
StatGraph.lnk
Metody probabilistyczne i statystyka
Model II
Badana cecha w populacji generalnej ma rozkład normalny N(
µ
,
σ
),
przy czym odchylenie standardowe w populacji
σ
jest nieznane. W
oparciu o wyniki
małej
n-elementowej próby zweryfikować hipotezę
zerową:
H
0
:
µ
=
µ
0
gdzie
µ
0
jest konkretną, hipotetyczną wartością średniej, wobec
hipotezy alternatywnej (dwustronnej):
H
1
:
µ
≠
µ
0
Wykład 5-6/ 12
StatGraph.lnk
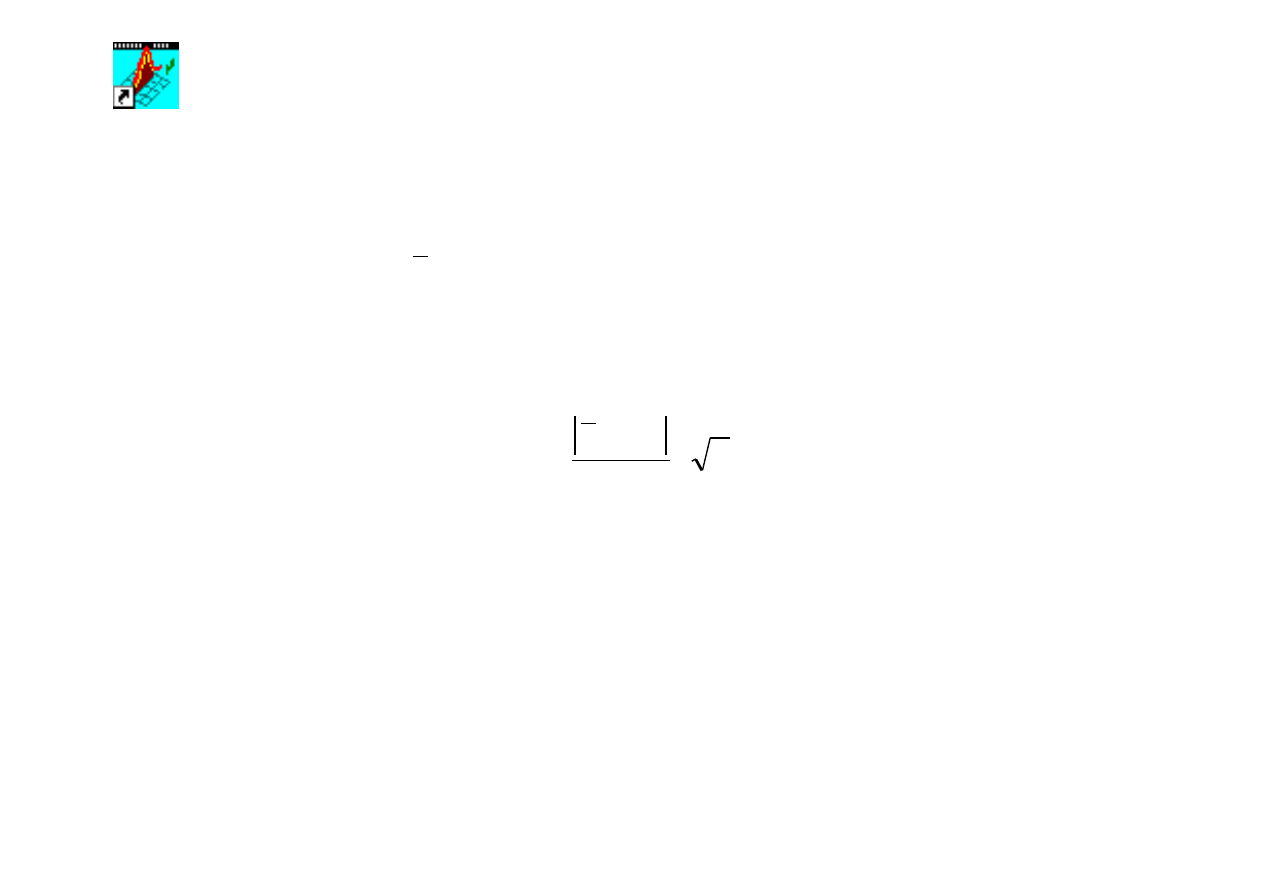
Metody probabilistyczne i statystyka
Test dla hipotezy zerowej jest następujący:
1. na podstawie wyników z próby oblicza się:
1.1.
wartość średnią
x
1.2.
odchylenie standardowe s
1.3.
wartość statystyki - zmiennej t wg wzoru:
n
s
x
t
⋅
−
=
0
µ
która przy prawdziwości hipotezy zerowej ma rozkład t-Studenta o
n-1 stopniach swobody
2.
z tablic rozkładu t-Studenta, dla ustalonego poziomu istotności
α
i dla
n-1 stopni swobody odczytuje się taką wartość t
α
, by zachodziło:
P(|T|
≥
t
α
) =
α
Wykład 5-6/ 13
StatGraph.lnk
Metody probabilistyczne i statystyka
Obszar krytyczny testu określony jest zależnością:
|T|
≥
t
α
tzn. że gdy z próby otrzymamy taką wartość t, że zachodzi:
|t|
≥
t
α
to hipotezę zerową H
0
odrzucamy. W przypadku przeciwnym, gdy
zachodzi:
|t|
<
t
α
nie ma podstaw do odrzucenia H
0
.
Wykład 5-6/ 14
StatGraph.lnk
Metody probabilistyczne i statystyka
Model III
Badana cecha w populacji generalnej ma rozkład normalny N(
µ
,
σ
)
lub dowolny inny, o średniej
µ
i skończonej i nieznanej wariancji
σ
. Na
podstawie wyników z
dużej
n-elementowej próby zweryfikować
hipotezę zerową:
H
0
:
µ
=
µ
0
gdzie
µ
0
jest konkretną, hipotetyczną wartością średniej, wobec
hipotezy alternatywnej (dwustronnej):
H
1
:
µ
≠
µ
0
Wykład 5-6/ 15
StatGraph.lnk
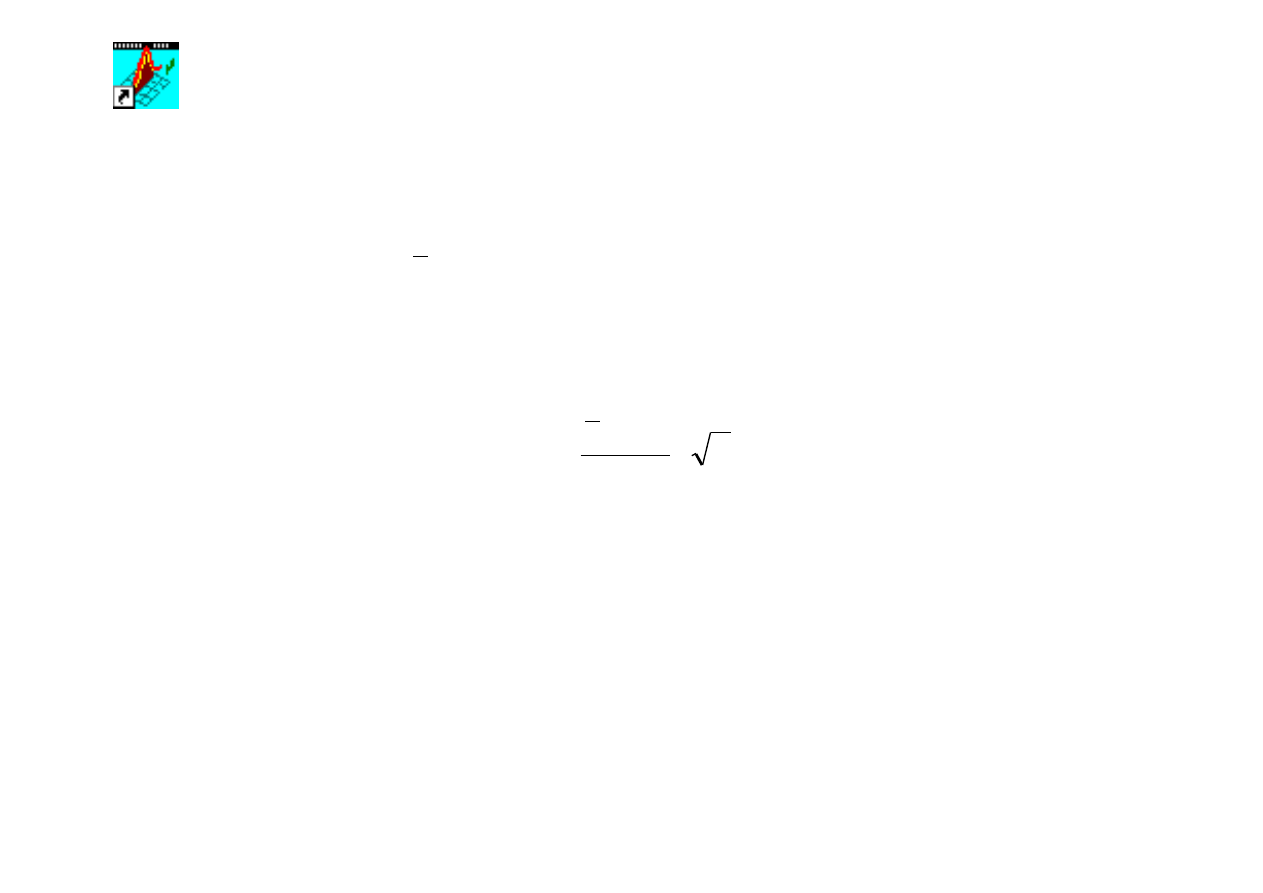
Metody probabilistyczne i statystyka
Test dla hipotezy zerowej jest następujący:
1. na podstawie wyników z próby oblicza się:
1.1.
wartość średnią
x
1.2.
odchylenie standardowe s
1.3.
wartość zmiennej standaryzowanej U wg wzoru:
n
s
x
u
⋅
−
=
0
µ
2.
z tablic rozkładu normalnego standaryzowanego N(0,1), dla
założonego poziomu istotności
α
wyznacza się wartość krytyczną
u
α
/2
, taką by zachodziło:
P(|U|
≥
u
α
/2
) =
α
Wykład 5-6/ 16
StatGraph.lnk
Metody probabilistyczne i statystyka
Obszar krytyczny testu określony jest zależnością:
|U|
≥
u
α
/2
tzn. że gdy z próby otrzymamy taką wartość u, że zachodzi:
|u|
≥
u
α
/2
to hipotezę zerową H
0
odrzucamy. W przypadku przeciwnym, gdy
zachodzi:
|u|
<
u
α
/2
nie ma podstaw do odrzucenia H
0
.
Wykład 5-6/ 17
StatGraph.lnk
Metody probabilistyczne i statystyka
Testy dla równości średnich dwóch populacji
Model I
Badamy dwie populacje generalne w których analizowane parametry
mają rozkłady normalne N(
µ
1
,
σ
1
) i N(
µ
2
,
σ
2
), przy czym znane są
odchylenia standardowe w tych populacjach
σ
1
i
σ
2
. W oparciu o wyniki
dwu niezależnych prób o liczebnościach odpowiednio n
1
i n
2
należy
sprawdzić słuszność hipotezy zerowej:
H
0
:
µ
1
=
µ
2
wobec hipotezy alternatywnej (dwustronnej):
H
1
:
µ
1
≠
µ
2
Test dla hipotezy zerowej jest następujący:
Wykład 5-6/ 18
StatGraph.lnk
Metody probabilistyczne i statystyka
1. na podstawie wyników z prób oblicza się:
1.1.
wartości średnie
1
x
i
2
x
1.2.
wartość zmiennej standaryzowanej U wg wzoru:
2
2
2
1
2
1
2
1
n
n
x
x
u
σ
σ
+
−
=
która przy prawdziwości hipotezy zerowej ma rozkład normalny
standaryzowany N(0,1)
2.
z tablic rozkładu normalnego standaryzowanego N(0,1), dla
założonego poziomu istotności
α
wyznacza się wartość krytyczną
u
α
/2
, taką by zachodziło:
P(|U|
≥
u
α
/2
) =
α
Wykład 5-6/ 19
StatGraph.lnk
Metody probabilistyczne i statystyka
Obszar krytyczny testu określony jest zależnością:
|U|
≥
u
α
/2
tzn. że gdy z próby otrzymamy taką wartość u, że zachodzi:
|u|
≥
u
α
/2
to hipotezę zerową H
0
odrzucamy. W przypadku przeciwnym, gdy
zachodzi:
|u|
<
u
α
/2
nie ma podstaw do odrzucenia H
0
.
Wykład 5-6/ 20
StatGraph.lnk
Metody probabilistyczne i statystyka
Model II
Badamy dwie populacje generalne w których analizowane parametry
mają rozkłady normalne N(
µ
1
,
σ
1
) i N(
µ
2
,
σ
2
), przy czym odchylenia
standardowe w tych populacjach
σ
1
i
σ
2
nie są znane ale jednakowe tj.
σ
1
=
σ
2
. W oparciu o wyniki dwu niezależnych
małych
prób o
liczebnościach odpowiednio n
1
i n
2
należy sprawdzić słuszność hipotezy
zerowej:
H
0
:
µ
1
=
µ
2
wobec hipotezy alternatywnej (dwustronnej):
H
1
:
µ
1
≠
µ
2
Wykład 5-6/ 21
StatGraph.lnk
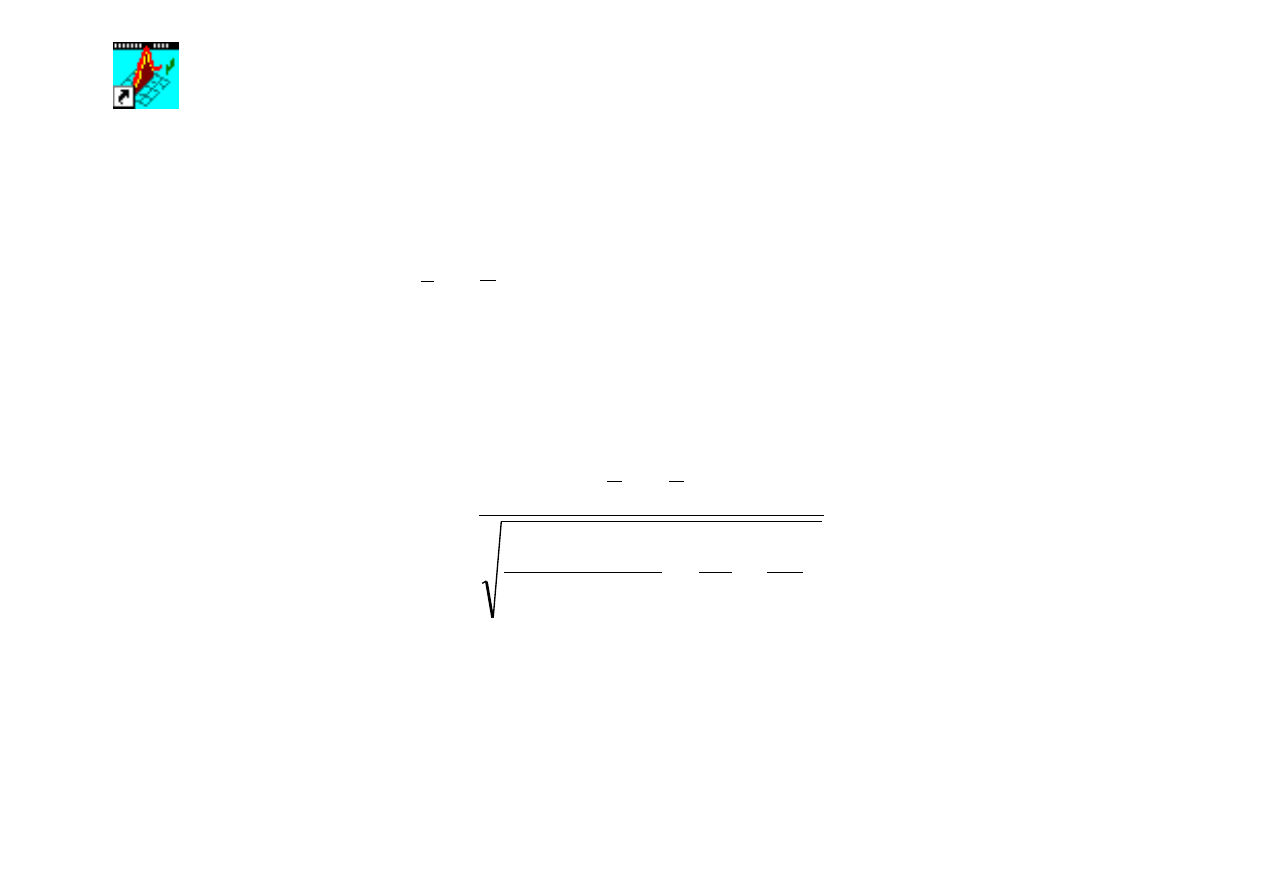
Metody probabilistyczne i statystyka
Test dla hipotezy zerowej jest następujący:
1. na podstawie wyników z prób oblicza się:
1.1.
wartości średnie
1
x
i
2
x
1.2.
wariancje
2
1
s
i
2
2
s
1.3.
wartość statystyki - zmiennej t wg wzoru:
+
⋅
−
+
+
−
=
2
1
2
1
2
2
2
2
1
1
2
1
1
1
2
n
n
n
n
s
n
s
n
x
x
t
która przy prawdziwości hipotezy zerowej ma rozkład t-Studenta o
(n
1
+n
2
-2) stopniach swobody
Wykład 5-6/ 22
StatGraph.lnk
Metody probabilistyczne i statystyka
2.
z tablic rozkładu t-Studenta, dla ustalonego poziomu istotności
α
i dla
n-1 stopni swobody odczytuje się taką wartość t
α
, by zachodziło:
P(|T|
≥
t
α
) =
α
Obszar krytyczny testu określony jest zależnością:
|T|
≥
t
α
tzn. że gdy z próby otrzymamy taką wartość t, że zachodzi:
|t|
≥
t
α
to hipotezę zerową H
0
odrzucamy.
W przypadku przeciwnym, gdy zachodzi:
|t|
<
t
α
nie ma podstaw do odrzucenia H
0
.
Wykład 5-6/ 23
StatGraph.lnk
Metody probabilistyczne i statystyka
Model III
Badamy dwie populacje generalne w których analizowane parametry
mają rozkłady normalne N(
µ
1
,
σ
1
) i N(
µ
2
,
σ
2
) lub inne o skończonych
wariancjach
2
1
σ
i
2
2
σ
, które są nieznane. W oparciu o wyniki dwu
niezależnych
dużych
prób o liczebnościach odpowiednio n
1
i n
2
należy
sprawdzić słuszność hipotezy zerowej:
H
0
:
µ
1
=
µ
2
wobec hipotezy alternatywnej (dwustronnej):
H
1
:
µ
1
≠
µ
2
Wykład 5-6/ 24
StatGraph.lnk
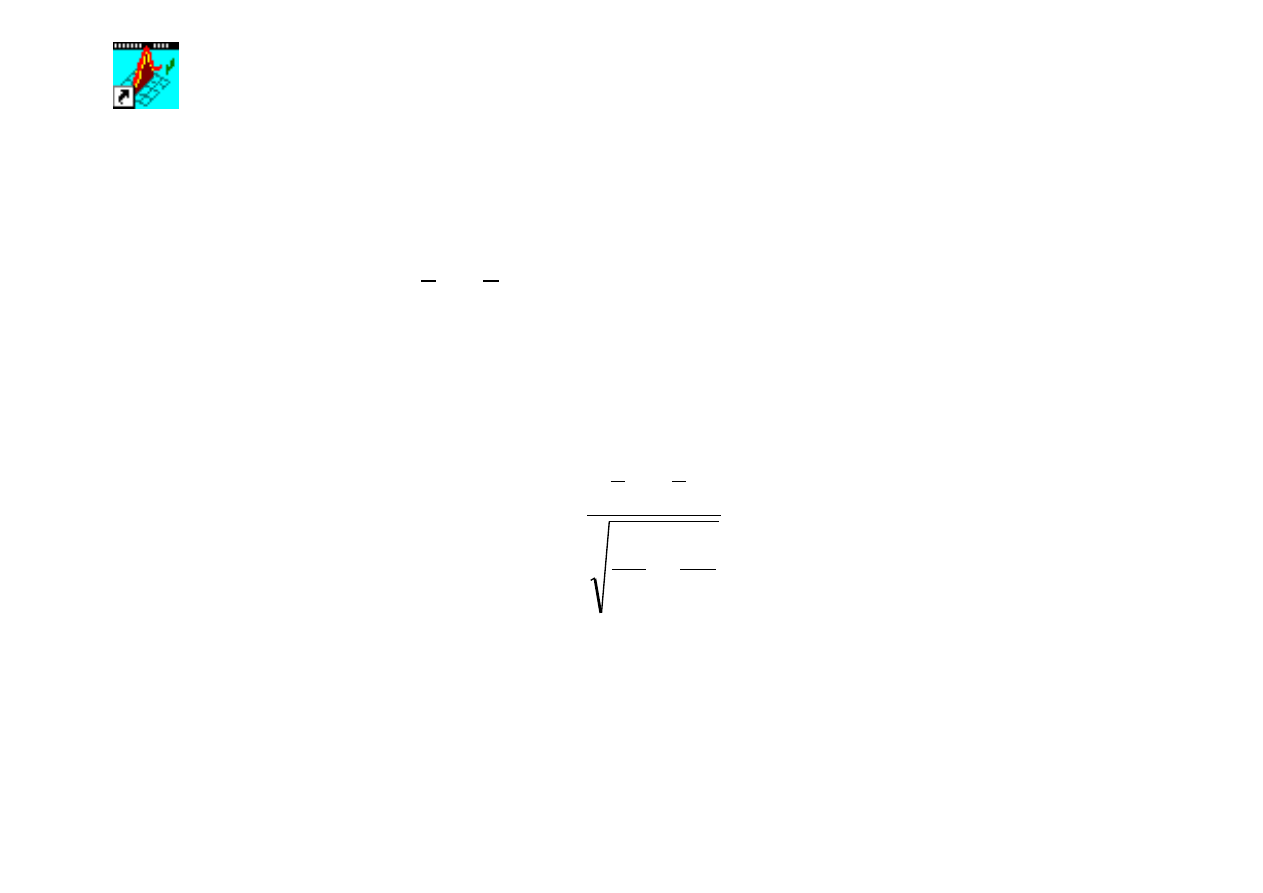
Metody probabilistyczne i statystyka
Test dla hipotezy zerowej jest następujący:
1. na podstawie wyników z prób oblicza się:
1.1.
wartości średnie
1
x
i
2
x
1.2.
wariancje
2
1
s
i
2
2
s
1.3.
wartość zmiennej standaryzowanej U wg wzoru:
2
2
2
1
2
1
2
1
n
s
n
s
x
x
u
+
−
=
która przy prawdziwości hipotezy zerowej ma rozkład normalny
standaryzowany N(0,1)
Wykład 5-6/ 25
StatGraph.lnk
Metody probabilistyczne i statystyka
2.
z tablic rozkładu normalnego standaryzowanego N(0,1), dla
założonego poziomu istotności
α
wyznacza się wartość krytyczną
u
α
/2
, taką by zachodziło:
P(|U|
≥
u
α
/2
) =
α
Obszar krytyczny testu określony jest zależnością:
|U|
≥
u
α
/2
tzn. że gdy z próby otrzymamy taką wartość u, że zachodzi:
|u|
≥
u
α
/2
to hipotezę zerową H
0
odrzucamy.
W przypadku przeciwnym, gdy zachodzi:
|u|
<
u
α
/2
nie ma podstaw do odrzucenia H
0
.
Wykład 5-6/ 26
StatGraph.lnk
Metody probabilistyczne i statystyka
Test dla wariancji populacji
W praktyce duża wariancja jest niekorzystna, gdyż oznacza dużą
niejednorodność analizowanej cechy, dlatego też przy weryfikacji
hipotez dotyczących wariancji przyjmuje się hipotezę alternatywną z
obszarem krytycznym prawostronnym.
Model
Badana cecha w populacji generalnej ma rozkład normalny N(
µ
,
σ
),
przy czym parametry
σ
i
µ
są nieznane. Na podstawie n-elementowej
próby zweryfikować hipotezę zerową:
H
0
:
2
σ
=
2
0
σ
gdzie
2
0
σ
jest konkretną, hipotetyczną wartością wariancji
Wykład 5-6/ 27
StatGraph.lnk
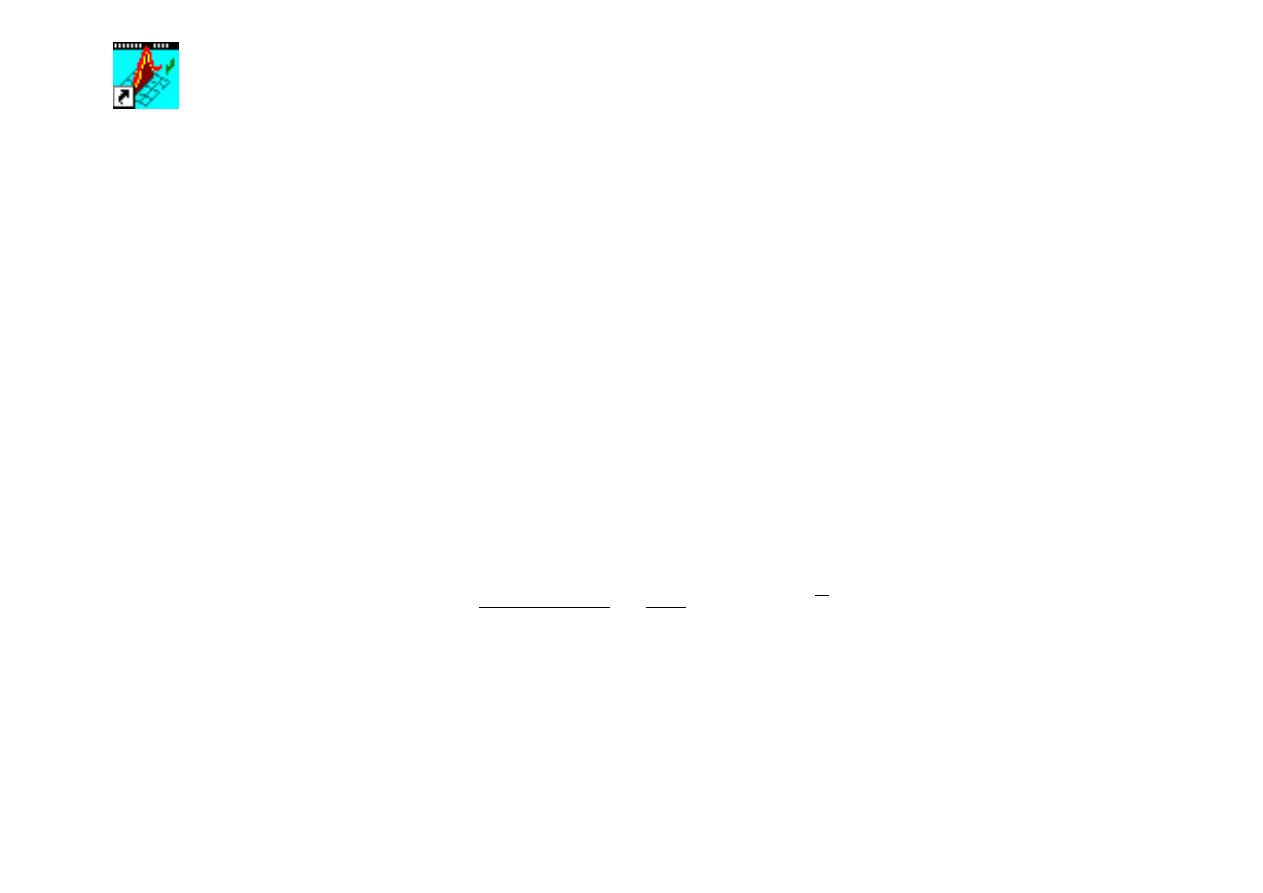
Metody probabilistyczne i statystyka
wobec hipotezy alternatywnej (prawostronnej):
H
1
:
2
σ
>
2
0
σ
Test dla hipotezy zerowej jest następujący:
1. na podstawie wyników z próby oblicza się:
1.1.
wariancję z próby s
2
1.2.
wartość zmiennej (statystyki)
χ
2
wg wzoru:
∑
=
−
⋅
=
⋅
−
=
n
i
i
x
x
s
n
1
2
2
0
2
0
2
2
)
(
1
)
1
(
σ
σ
χ
która przy prawdziwości hipotezy zerowej ma rozkład
χ
2
(chi-
kwadrat) o (n-1) stopniach swobody
Wykład 5-6/ 28
StatGraph.lnk
Metody probabilistyczne i statystyka
2.
z tablic rozkładu
χ
2
(chi-kwadrat) dla założonego poziomu istotności
α
i (n-1) stopni swobody wyznacza się wartość krytyczną
2
α
χ
, taką
by zachodziło:
(
)
α
=
χ
≥
χ
α
2
2
P
Nierówność:
2
2
α
χ
≥
χ
określa prawostronny obszar krytyczny odrzuceń, tzn. gdy jest
spełniona to należy odrzucić hipotezę zerową H
0
na rzecz hipotezy
alternatywnej H
1
.
Wykład 5-6/ 29
StatGraph.lnk
Metody probabilistyczne i statystyka
Test dla równości wariancji dwóch populacji
W praktyce sytuacja taka pojawia się, gdy zachodzi potrzeba
sprawdzania hipotezy o jednakowym stopniu rozproszenia badanej
cechy w dwu populacjach. Zakład się, że badane populacje mają
normalny rozkład analizowanej cechy.
Model
Rozpatrujemy dwie populacje, w których badana cecha ma
odpowiednio rozkład normalny N(
µ
1
,
σ
1
) i N(
µ
2
,
σ
2
), przy czym parametry
tych rozkładów są nieznane. W oparciu o wyniki dwu niezależnych prób
o liczebnościach odpowiednio n
1
i n
2
należy sprawdzić słuszność
hipotezy zerowej:
H
0
:
2
1
σ
=
2
2
σ
Wykład 5-6/ 30
StatGraph.lnk
Metody probabilistyczne i statystyka
wobec hipotezy alternatywnej (dwustronnej):
H
1
:
2
1
σ
≠
2
2
σ
Test dla hipotezy zerowej jest następujący:
1. na podstawie wyników z próby oblicza się:
1.1.
wariancje z prób
2
1
s
i
2
2
s
, przy czym musi zachodzić
2
1
s
>
2
2
s
,
1.2.
wartość zmiennej (statystyki) F wg wzoru:
2
2
2
1
s
s
F
=
która ma rozkład F-Snedecora z (n
1
-1, n
2
-1) stopniami swobody.
Wykład 5-6/ 31
StatGraph.lnk
Metody probabilistyczne i statystyka
2.
z tablic rozkładu F-Snedecora dla założonego poziomu istotności
α
odczytuje się wartość krytyczną F
α
, taką by zachodziło:
P(F
≥
F
α
) =
α
Nierówność:
F
≥
F
α
określa prawostronny obszar krytyczny w teście, tzn.
dla
F
≥
F
α
→
odrzucamy hipotezę zerową H
0
na rzecz hipotezy
alternatywnej H
1
a dla
F
<
F
α
→
przyjmujemy hipotezę zerową H
0
Wykład 5-6/ 32
StatGraph.lnk
Metody probabilistyczne i statystyka
Testy nieparametryczne
Dotyczą postaci rozkładów - tzn. weryfikuje się hipotezę o postaci
funkcyjnej rozkładu populacji generalnej.
Warunki przeprowadzenia testów nieparametrycznych
-
liczebność próby jest duża
-
próba jest losowa
-
poziom istotności nie mniejszy niż 0,01
W celu zweryfikowania hipotezy o postaci rozkładu bada się
zgodność rozkładu empirycznego uzyskanego z próby z rozkładem
teoretycznym (hipotetycznym).
Wykład 5-6/ 33
StatGraph.lnk
Metody probabilistyczne i statystyka
Model
Populacja generalna ma dowolny rozkład o dystrybuancie należącej
do pewnego zbioru
Ω
rozkładów o określonym typie postaci funkcyjnej
dystrybuanty. Z populacji tej wylosowano dużą próbę (
n>30
), której
wyniki podzielono na
r
rozłącznych klas o liczebnościach
m
i
w każdej
klasie, przy czym:
∑
=
=
r
1
i
i
n
n
Otrzymano w ten sposób
szereg rozdzielczy
.
Wykład 5-6/ 34
StatGraph.lnk
Metody probabilistyczne i statystyka
Na podstawie wyników z tej próby należy sprawdzić hipotezę
H
0
, że
populacja generalna ma rozkład typu
Ω
, tzn:
H
0
: F(x)
∈
Ω
Gdzie F(x) jest dystrybuantą rozkładu populacji.
Wykład 5-6/ 35
StatGraph.lnk
Metody probabilistyczne i statystyka
Test zgodności
Wprowadza się charakterystykę, będącą miarą odległości między
dystrybuantą rozkładu empirycznego a dystrybuantą rozkładu
hipotetycznego:
∑
=
⋅
⋅
−
=
χ
r
1
i
i
2
i
i
2
p
n
)
p
n
(n
gdzie:
n
i
- liczebność empiryczna i-tego przedziału klasowego (nie
powinna być mniejsza niż 10)
r
- liczba przedziałów klasowych
p
i
- prawdopodobieństwo (częstość teoretyczna) odpowiadające
wartość badanej cechy w i-tej klasie:
Wykład 5-6/ 36
StatGraph.lnk
Metody probabilistyczne i statystyka
∑
=
=
r
1
i
i
1
p
n
⋅
p
i
- liczebność teoretyczna (oczekiwana) w i-tym przedziale:
∑
=
=
r
1
i
i
n
n
Statystyka
χ
2
ma przy założeniu prawdziwości
H
0
i przy
n
→
∞
rozkład
χ
2
o
r
stopniach swobody lub o (
r-k-1
) stopniach swobody, gdy
na podstawie próby oszacowano
k
parametrów.
Utworzony szereg rozdzielczy jest rozkładem empirycznym.
Wykład 5-6/ 37
StatGraph.lnk
Metody probabilistyczne i statystyka
Jako rozkład teoretyczny najczęściej przyjmuje się:
•
rozkład dwumianowy (Bernoulliego)
•
rozkład Poissona
•
rozkład normalny
Obliczoną statystykę
χ
2
należy porównać z wartością krytyczną
χ
α
2
odczytaną z tablic rozkładu chi-kwadrat , przy ustalonym poziomie
istotności
α
i określonej liczbie stopni swobody.
Obszar krytyczny w tym teście buduje się prawostronnie, tzn. tak
aby była spełniona relacja:
α
χ
χ
α
=
≥
)
(
2
2
P
Wykład 5-6/ 38
StatGraph.lnk
Metody probabilistyczne i statystyka
Jeżeli zachodzi:
2
2
α
χ
≥
χ
to
H
0
należy odrzucić (gdyż różnica między rozkładem empirycznym
a hipotetycznym jest statystycznie istotna)
Wykład 5-6/ 39
StatGraph.lnk
Document Outline