1
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Modelowanie i symulacja
dr inż. Piotr Piela
Zakład Metod Matematycznych
kontakt: pokój 28
ppiela@wi.ps.pl
1
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Modelowanie i symulacja
dr inż. Piotr Piela
Zakład Metod Matematycznych
kontakt: pokój 28
ppiela@wi.ps.pl
2
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Równania Eulera-Lagrange'a
Model dynamiczny – zasada najmniejszego działania
d
dt
∂ L
∂ ˙q
k
− ∂
L
∂ q
k
=Q
k
k=1, N
N
- liczba
stopni swobody systemu
–
równa liczbie współrzędnych
uogólnionych (liczbie prędkości uogólnionych)
˙q
k
q
k
Q
k
-
współrzędne
uogólnione
,
opisujące
system
po
wyeliminowaniu zmiennych zależnych
-
prędkości uogólnione
.
-
siła uogólniona
związana ze współrzędną uogólnioną
q
k
-
funkcja Lagrange'a
L
=Lq , ˙q ,t
3
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Równania Eulera-Lagrange'a
Model dynamiczny – zasada najmniejszego działania
d
dt
∂ L
∂ ˙q
k
− ∂
L
∂ q
k
=Q
k
k=1, N
L
=T −U
Dla konserwatywnych systemów mechanicznych funkcja Lagrange'a
jest różnicą między energią kinetyczną
T
a energią potencjalną
U
systemu.
Ostatecznie równania Eulera-Lagrange'a przyjmie postać:
d
dt
∂T
∂ ˙q
k
− ∂
T
∂ q
k
∂
U
∂ q
k
=Q
k
NP
k=1, N
4
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – zasada najmniejszego działania
Równania Eulera-Lagrange'a tworzą układ
N
równań różniczkowych
zwyczajnych rzędu drugiego. Równanie te uzupełnione o
2N
warunków początkowych jednoznacznie określają równania ruchu
konserwatywnego systemu mechanicznego. Wyrażają one drugie
prawo Newtona równowagi sił.
5
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
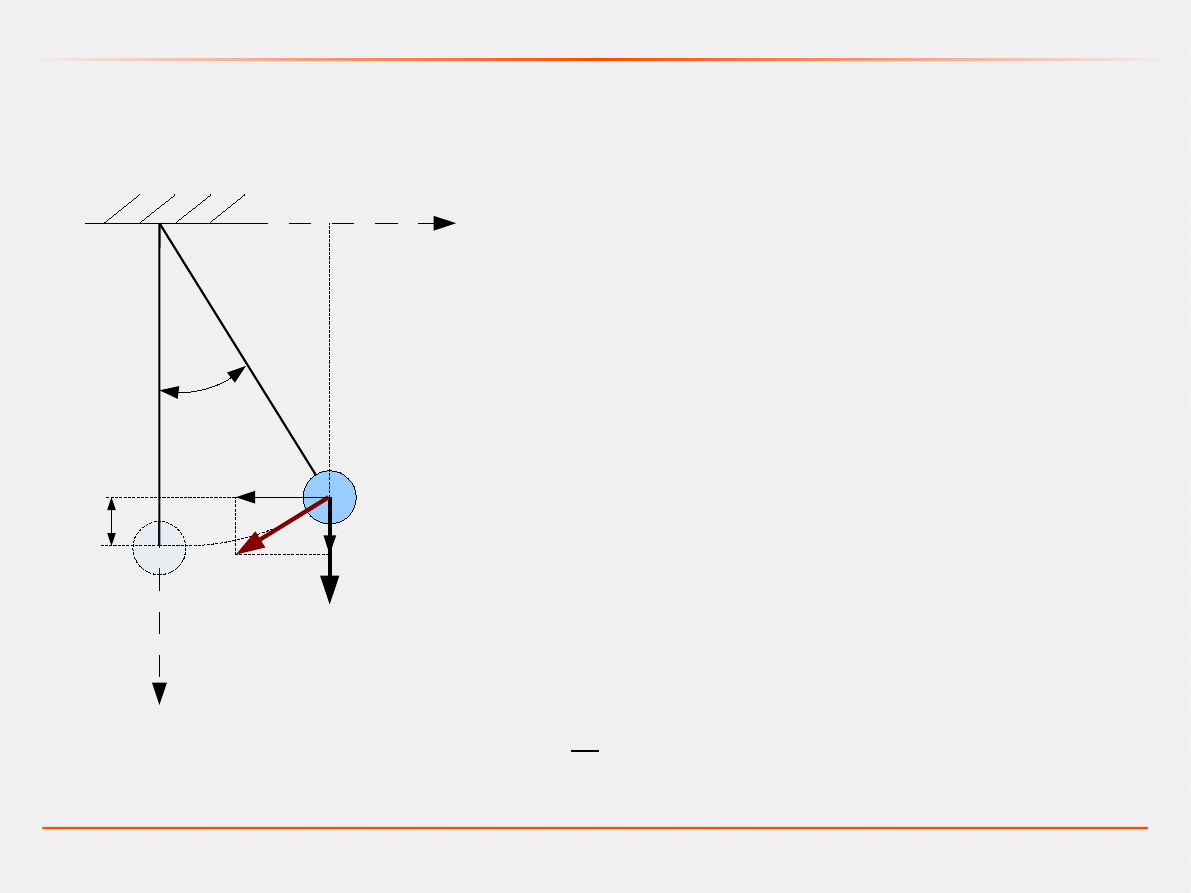
Przykład: Model wahadła bez tłumienia
Model dynamiczny – zasada najmniejszego działania
m
– masa,
l – długość,
φ
– kąt wychylenia wahadła,
g – przyspieszenie ziemskie,
v – prędkość
l
X
Y
x
y
l-y
φ
mg
v
v
y
v
x
x
=lsin
y
=lcos
Energia kinetyczna układu:
T
=
1
2
mv
2
6
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
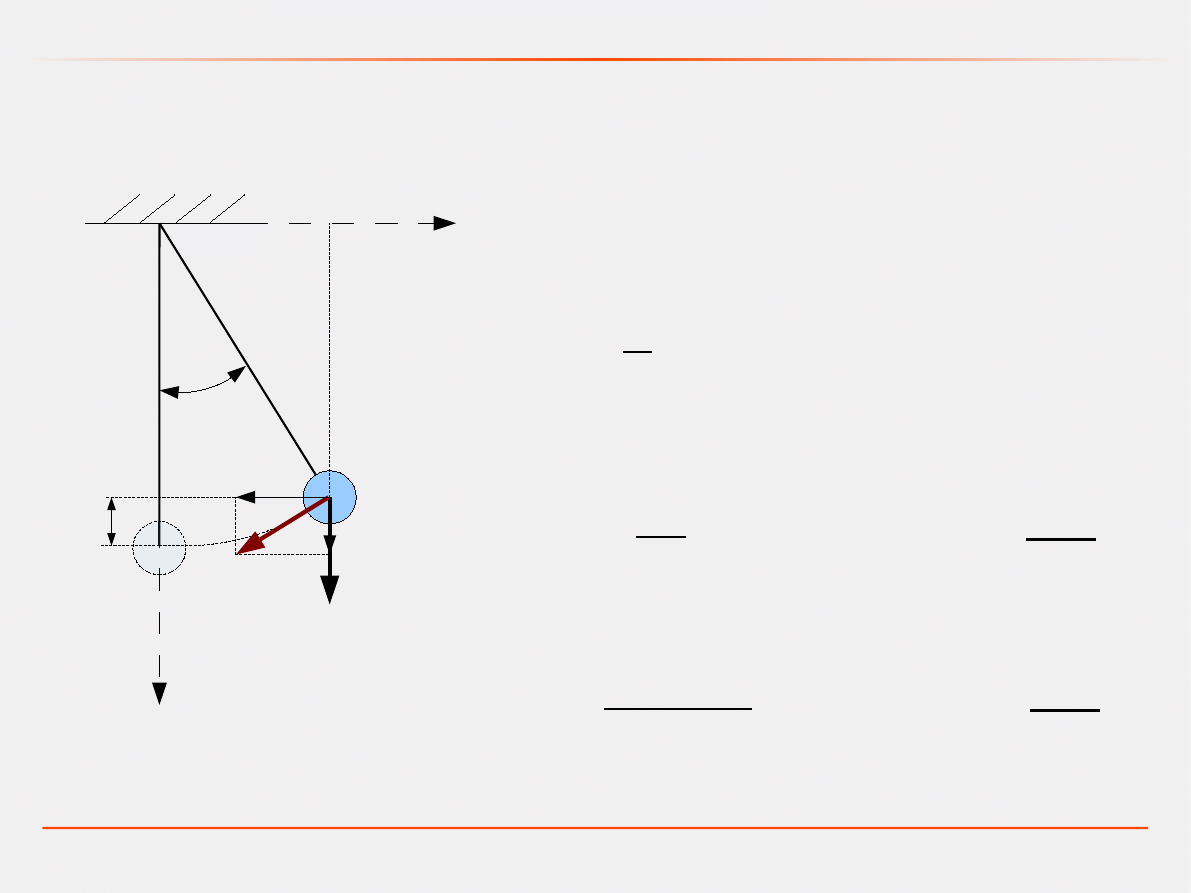
Model dynamiczny – zasada najmniejszego działania
l
X
Y
x
y
l-y
φ
mg
v
v
y
v
x
x
=lsin y=lcos
Energia kinetyczna układu:
T
=
1
2
mv
2
v
2
=v
x
2
v
y
2
v
x
=−
dx
dt
v
y
=
d
l− y
dt
v
x
=−lcos
d
dt
v
y
=lsin
d
dt
7
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
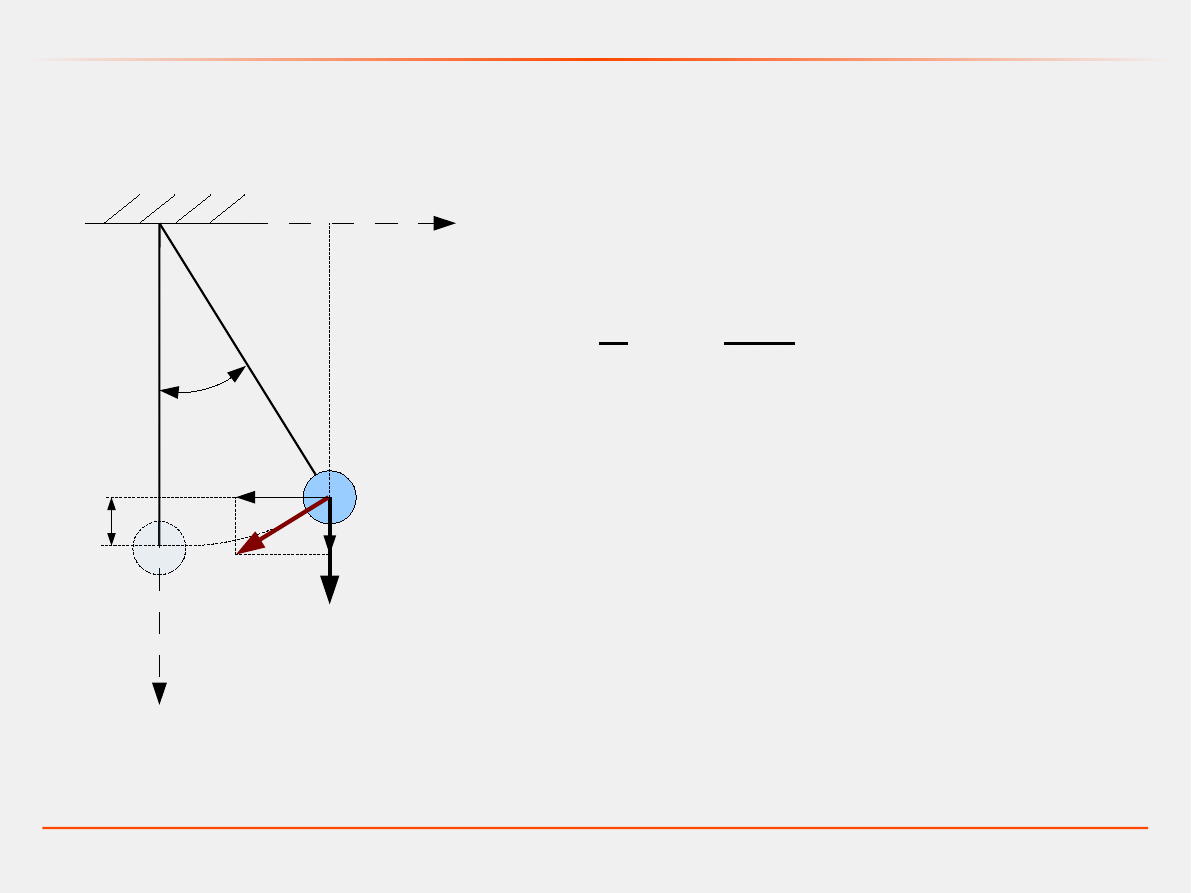
Model dynamiczny – zasada najmniejszego działania
l
X
Y
x
y
l-y
φ
mg
v
v
y
v
x
Po podstawieniu energia kinetyczna
układu wynosi:
T
=
1
2
ml
2
d
dt
2
Energia potencjalna układu:
U
=mg l−l cos
8
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
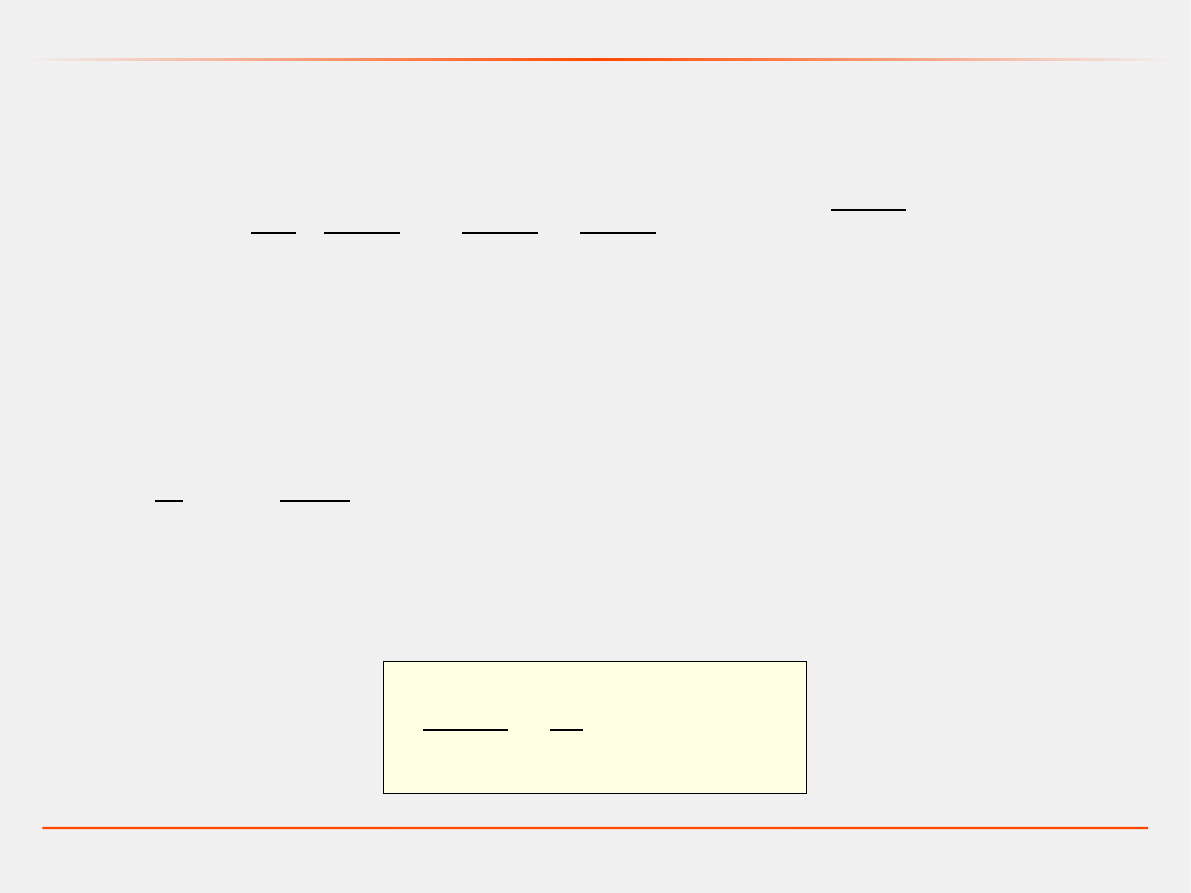
Równania Eulera-Lagrange'a – bez zewnętrznych sił niepotencjalnych
Model dynamiczny – zasada najmniejszego działania
d
dt
∂T
∂ ˙q
k
− ∂
T
∂ q
k
∂
U
∂ q
k
=0 k=1, N
Dla wahadła:
T
=
1
2
ml
2
d
dt
2
U
=mg l−l cos
- energia kinetyczna
- energia potencjalna
ostatecznie:
d
2
dt
2
g
l
sin
=0
q
=
- współrzędna uogólniona
9
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Równania Eulera-Lagrange'a dla wahadła – równanie II rzędu:
Model dynamiczny – zasada najmniejszego działania
d
2
dt
2
g
l
sin
=0
Równania stanu – równania I rzędu:
{
d
1
dt
=
2
d
2
dt
=−
g
l
sin
1
10
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
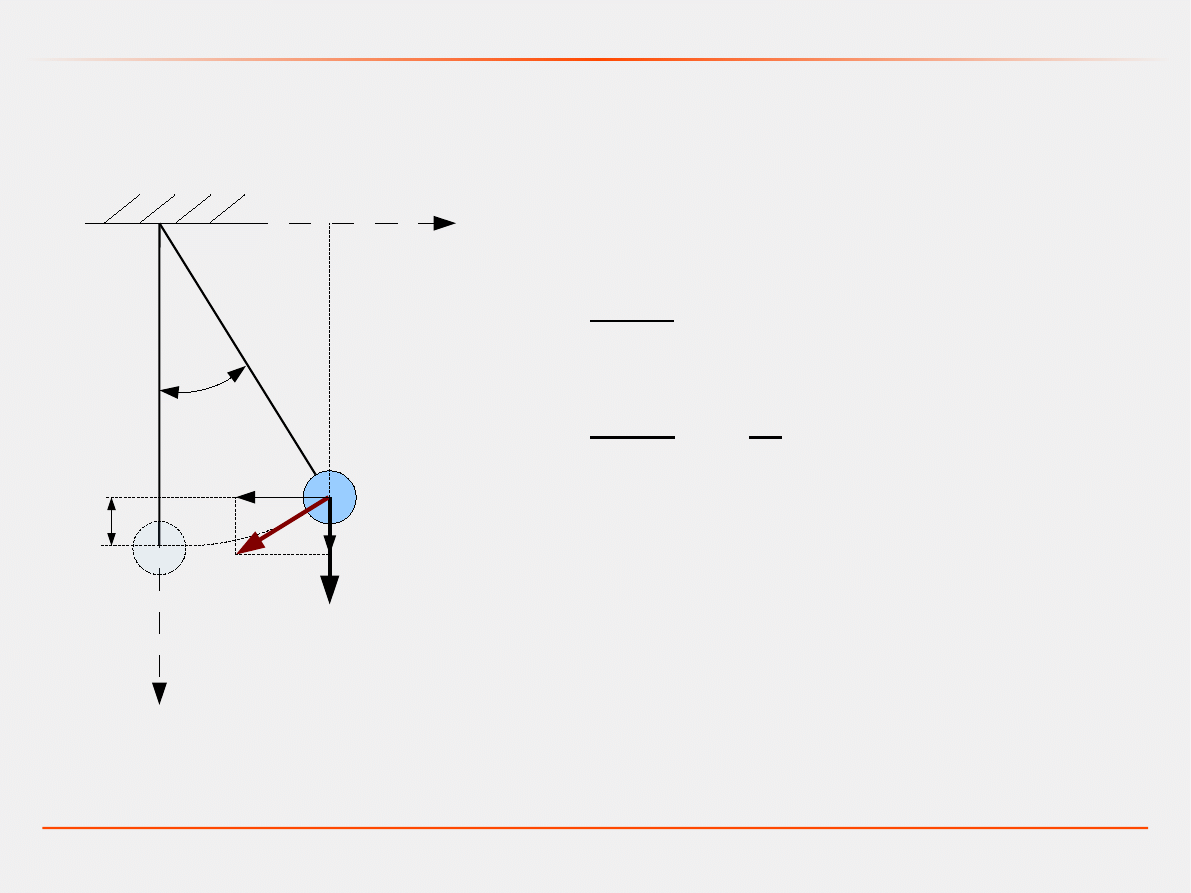
Przykład: Model wahadła bez tłumienia
Model dynamiczny – zasada najmniejszego działania
l
X
Y
x
y
l-y
φ
mg
v
v
y
v
x
Równania stanu:
Równania wyjścia:
{
d
1
dt
=
2
d
2
dt
=−
g
l
sin
1
{
y
1
t=
1
t
y
2
t=
2
t
11
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
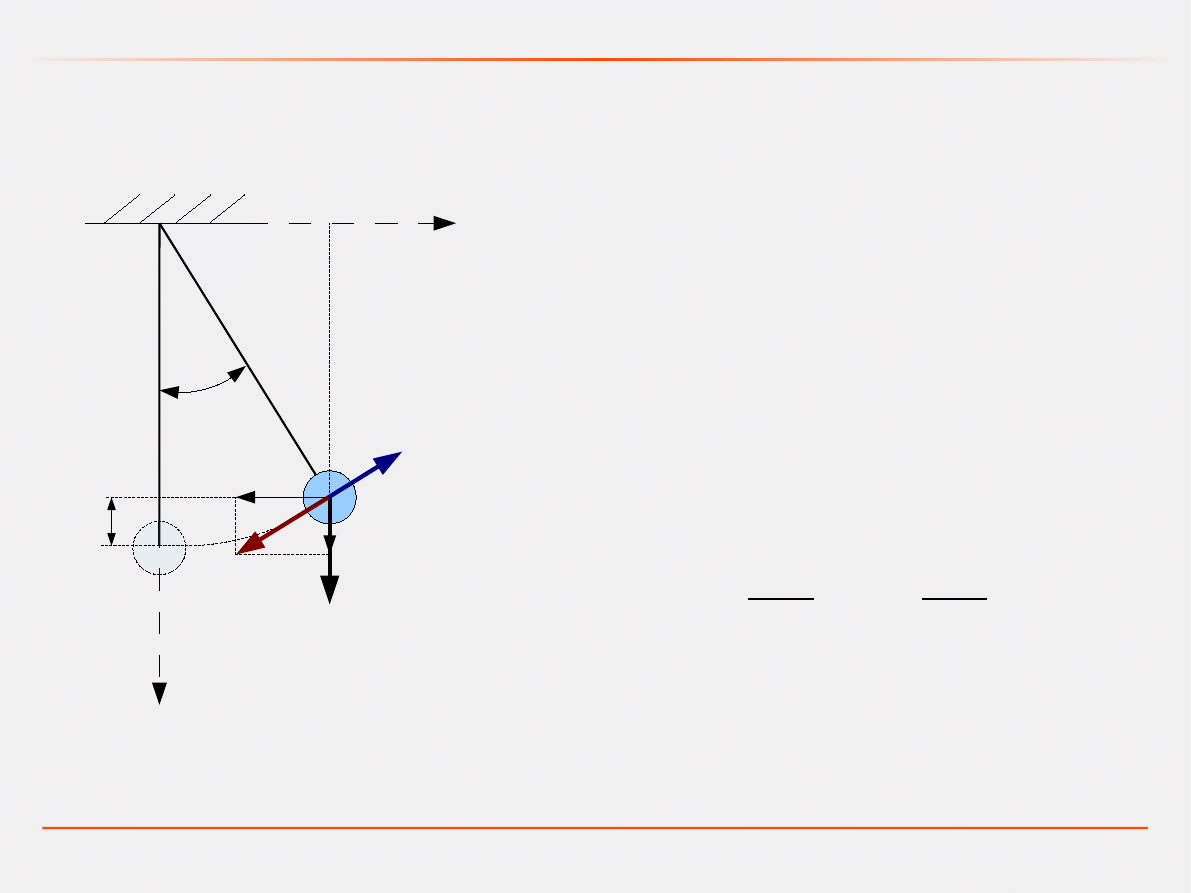
Przykład: Model wahadła z tłumieniem
Model dynamiczny – zasada najmniejszego działania
l
X
Y
x
y
l-y
φ
mg
v
v
y
v
x
F
Siła tłumiąca:
F
=−b v
F
x
=−b v
x
=−b ˙x
F
y
=−b v
y
=−b ˙y
- współrzędna uogólniona
Q
=F
x
⋅∂
x
∂
F
y
⋅∂
y
∂
12
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Równania Eulera-Lagrange'a – z zewnętrznymi siłami niepotencjalnymi
Model dynamiczny – zasada najmniejszego działania
d
dt
∂T
∂ ˙q
k
− ∂
T
∂ q
k
∂
U
∂ q
k
=Q
k
NP
k=1, N
T
=
1
2
ml
2
d
dt
2
U
=mg l−l cos
- energia kinetyczna
- energia potencjalna
ostatecznie:
¨ b
m
˙ g
l
sin
=0
Q
=−b l
2
˙
13
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
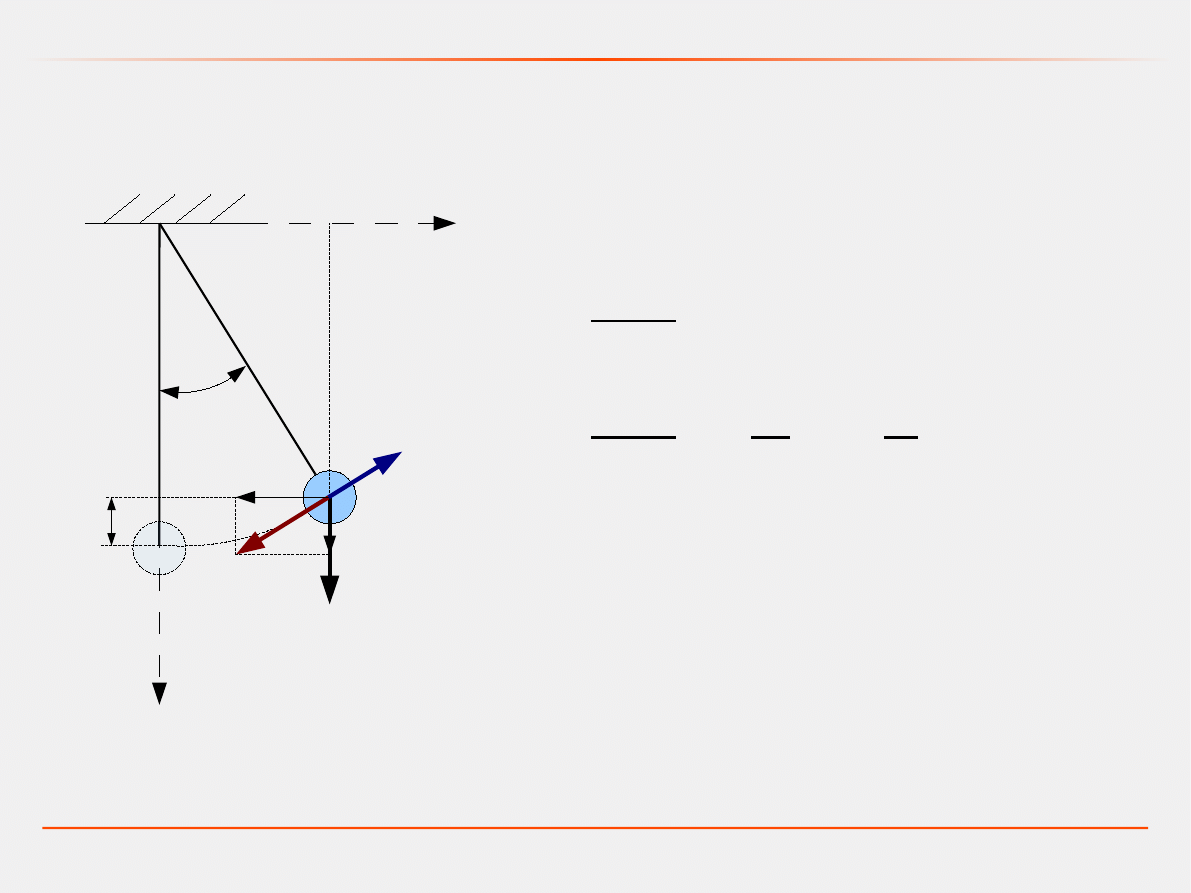
Przykład: Model wahadła z tłumieniem
Model dynamiczny – zasada najmniejszego działania
Równania stanu:
Równania wyjścia:
{
d
1
dt
=
2
d
2
dt
=−
b
m
2
−
g
l
sin
1
{
y
1
t=
1
t
y
2
t=
2
t
l
X
Y
x
y
l-y
φ
mg
v
v
y
v
x
F
14
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – zasada najmniejszego działania
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
t
φ
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
t
φ
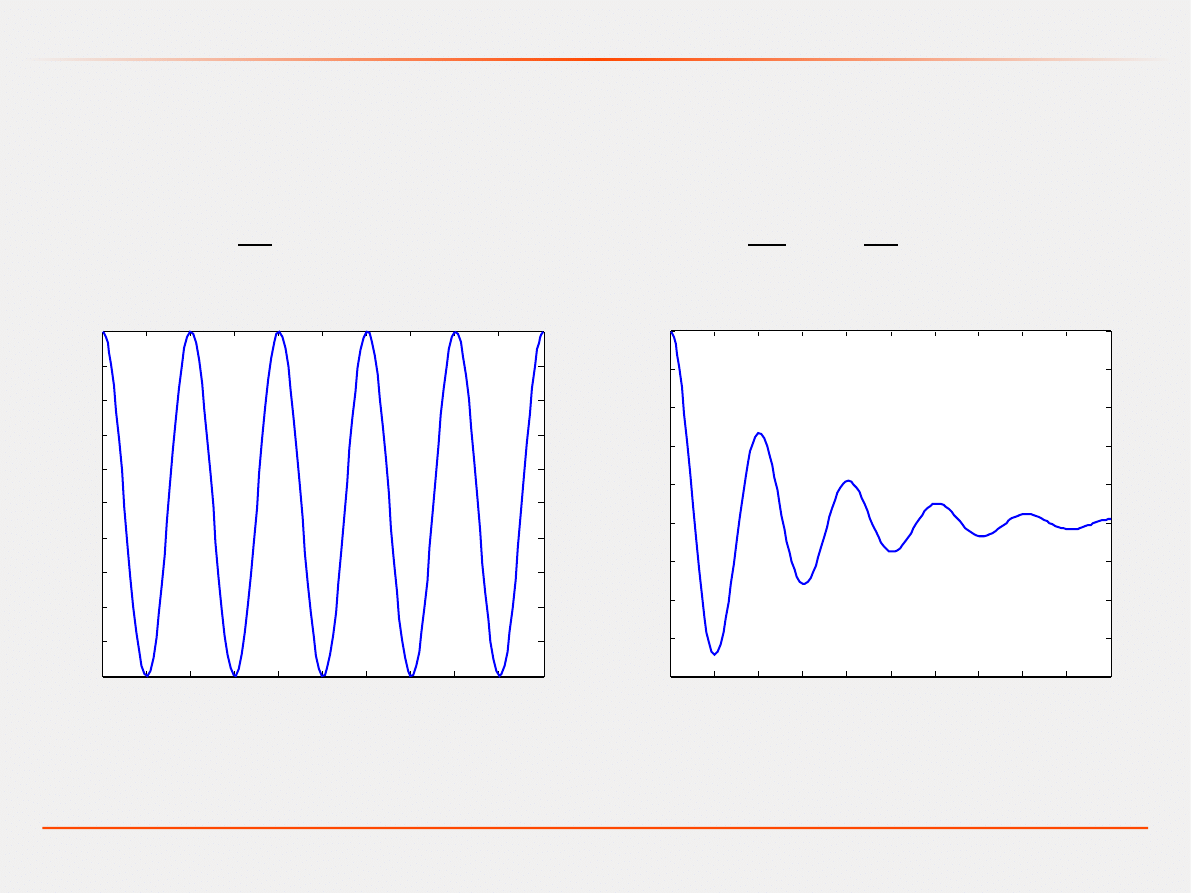
Model wahadła z tłumieniem
Model wahadła bez tłumienia
¨ b
m
˙ g
l
sin
=0
¨ g
l
sin
=0
15
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – normalna postać równań
W rezultacie wykorzystania metody najmniejszego działania
otrzymujemy równania systemu dynamicznego w postaci:
{
¨q
1
=
1
q
1,
, q
N
, ˙q
1,
, ˙q
N
, u
1
t ,, u
m
t
⋯
¨q
N
=
N
q
1,
, q
N
, ˙q
1,
, ˙q
N
,u
1
t , , u
m
t
W przestrzeni stanów system opisuje normalna postać równań
dynamicznych. Jest to układ równań różniczkowych pierwszego
rzędu.
{
˙x
1
= f
1
q
1,
, q
P
, ˙q
1,
, ˙q
P
, u
1
t , ,u
m
t
⋯
˙x
P
= f
P
q
1,
, q
P
, ˙q
1,
, ˙q
P
, u
1
t , , u
m
t
16
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – normalna postać równań
Stosując podstawienie:
q
1
=x
1,
q
N
=x
N
,
˙q
1
= y
N
1
,
, ˙q
N
=x
P
gdzie P
=2N
możemy z równań Lagrange'a otrzymać normalną postać równań
dynamicznych systemu.
Przykład:
¨qaq=bu
podstawienie:
q
=x
1
˙q= ˙x
1
=x
2
¨q= ˙x
2
normalna postać równań:
{
˙x
1
=x
2
˙x
2
=bu−ax
1
17
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
Metody rozwiązywania równań różniczkowych:
metody analityczne,
rozwiązania ogólne
rozwiązania szczególne
metody numeryczne,
rozwiązania szczególne
metody eksperymentalne
rozwiązania szczególne
18
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
Rozwiązaniem równania różniczkowego
nazywamy każdą funkcję
y=y(x)
spełniającą to równanie w pewnym przedziale. Każde
rozwiązanie, które zawiera
n
dowolnych stałych c
1
, c
2
, ... , c
n
, tak że
możemy na nie nałożyć
n
dodatkowych warunków początkowych,
nazywamy
rozwiązaniem ogólnym
. Jeśli ustalimy wartości tych
stałych to otrzymamy
rozwiązanie szczególne
.
19
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
Przykład: Chcemy rozwiązać równanie
˙0=0
0=1
Jest to przypadek równania różniczkowego liniowego o stałych
współczynnikach
¨y p ˙yqy=0,
którego równanie charakterystyczne ma postać:
r
2
p rq=0
dla
¨40⋅=0
r
2
40=0
0
r
1
= j
40
r
2
=− j
40
y
=e
x
C
1
sin
xC
2
cos
x
r
1
= j
r
2
=− j
=0
=
40
=C
1
sin
40t
C
2
cos
40 t
rozwiązanie ogólne
0
¨40⋅=0
20
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
¨40=0
Przykład: Chcemy rozwiązać równanie
˙0=0
0=1
Rozwiązanie ogólne:
Z warunków początkowych wyznaczamy C
1
i C
2
0=C
1
sin
40
⋅0C
2
cos
40
⋅0=1 C
2
=1
˙=
40
⋅C
1
cos
40t
−
40
⋅C
2
sin
40 t
˙0=
40
⋅C
1
cos
40
⋅0−
40
⋅C
2
sin
40
⋅0=0 C
1
=0
Rozwiązanie szczególne:
=cos
40 t
=C
1
sin
40t
C
2
cos
40 t
21
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
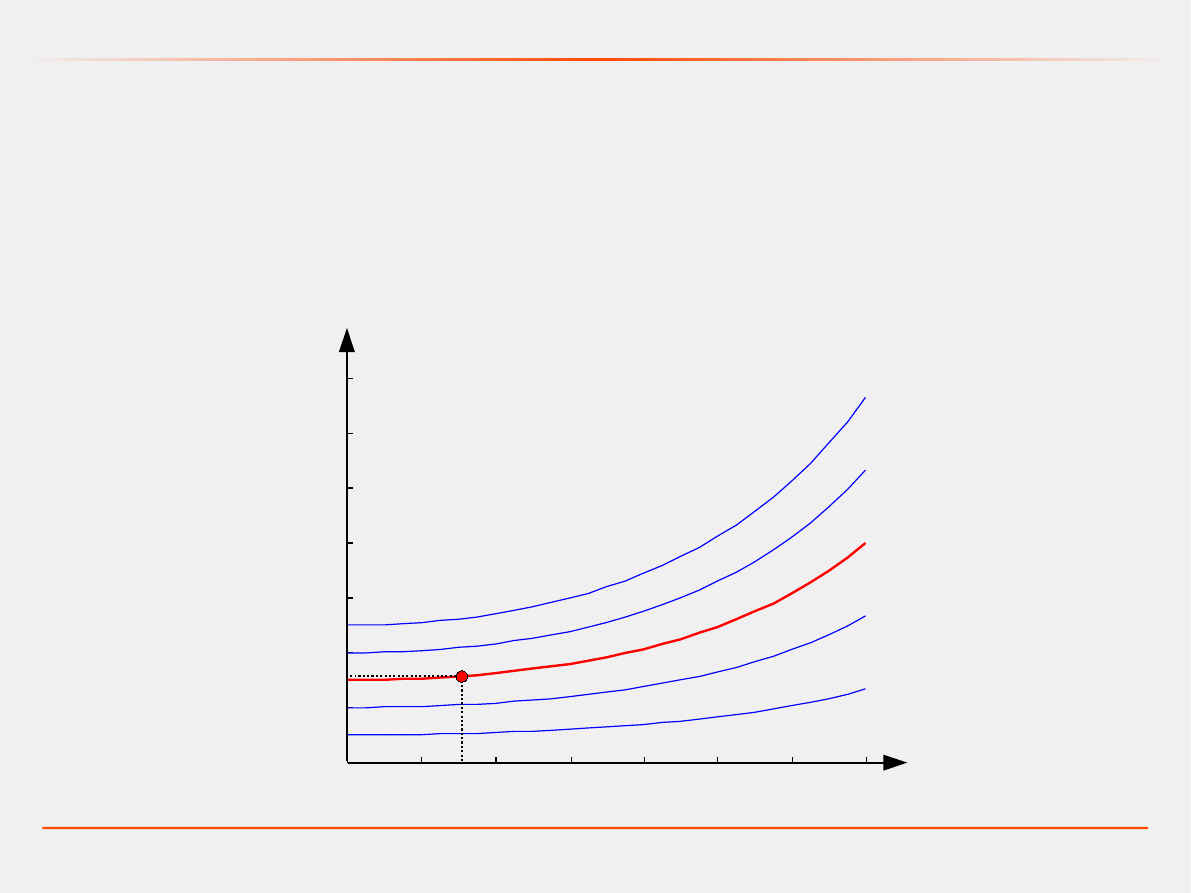
METODY NUMERYCZNE
jednokrokowe
wielokrokowe
ze stałym krokiem
ze zmiennym krokiem
I-go rzędu
II-go rzędu
...
n-tego rzędu
I-go rzędu
II-go rzędu
...
n-tego rzędu
22
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
Rozpatrujemy równanie różniczkowe w postaci:
˙y= f x , y
z warunkiem początkowym:
y
x
0
= y
0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0
1
2
3
4
5
6
7
x
y
x
0
y
0
23
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
Metoda Eulera
(często nazywana metodą siecznych ze względu na
interpretację geometryczną) jest najprostszą z metod rozwiązywania
równań różniczkowych zwyczajnych. Kolejne rozwiązania wyznacza
się na podstawie zależności:
Przybliżenie wartości ścisłej y(x
n
) ma błąd rzędu h
2
. Metoda ta
pomimo swej prostoty jest rzadko stosowana ze względu na bardzo
wolną zbieżność. Istnieją szybciej zbieżne modyfikacje metody
Eulera (ulepszona metoda Eulera i zmodyfikowana metoda Eulera),
ale obliczenie jednego kroku to ponad dwukrotnie większy koszt w
porównaniu z wersją podstawową.
y
n
1
= y
n
f x
n
, y
n
⋅h , n1
24
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
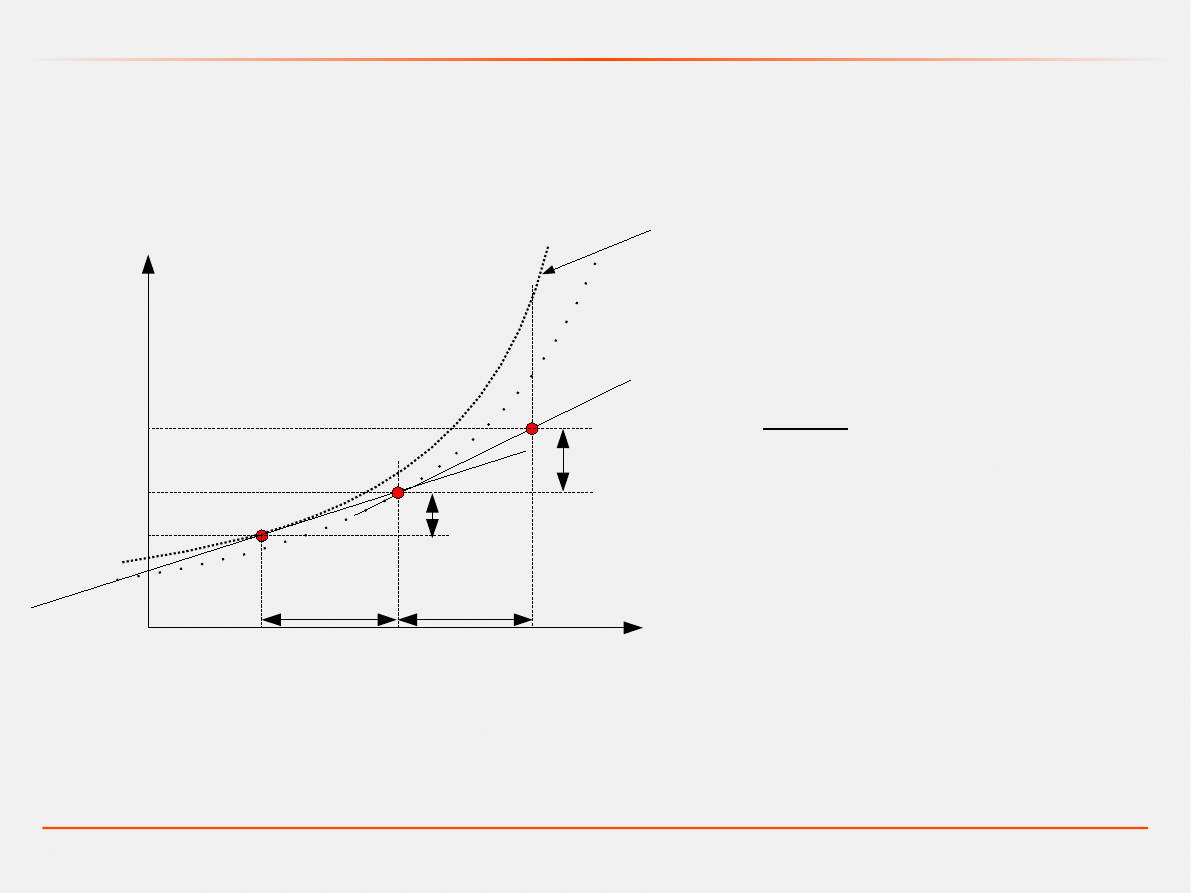
Metoda Eulera
y
n
1
= y
n
f x
n
, y
n
⋅h
x
y
y
0
rozwiązanie dokładne
y=f
(x
1
,y
1
)
h=
∆
x
1
∆
y
1
y
1
= y
0
y
1
y
1
x
1
= f x
0,
y
0
y
1
= y
0
f x
0,
y
0
x
1
y
1
x
0
h=
∆
x
2
x
1
y
2
x
2
∆
y
2
y=f(x
0
,y
0
)
x
1
=h
y
1
= y
0
f x
0,
y
0
h
25
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
Metody Rungego-Kutty –
mogą osiągać różne rzędy dokładności.
Najczęściej stosuje się metodę IV rzędu dokładności:
y
n
1
= y
n
1
6
K
1
2K
2
2K
3
K
4
K
1
= f x
n
, y
n
⋅h
K
2
= f x
n
h/2, y
n
1/ 2⋅K
1
⋅h
K
3
= f x
n
h/ 2, y
n
1/2⋅K
2
⋅h
K
4
= f x
n
h , y
n
K
3
⋅h
26
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
Metoda
Adams’a-Bashfort’a
należy
do
grupy
metod
wielokrokowych, w których wykorzystuje się informacje o
poprzednio obliczonych wartościach funkcji. W sytuacji gdy
korzystamy z informacji w dwóch punktach otrzymamy metodę
dwukrokową:
y
n
1
= y
n
h
2
3f x
n
, y
n
− f x
n
−1
, y
n
−1
27
MODELOWANIE I SYMULACJA
Szczecin - 2006-12-08
Model dynamiczny – rozwiązywanie równań stanu
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
-5
-4
-3
-2
-1
0
1
2
3
4
5
t
φ
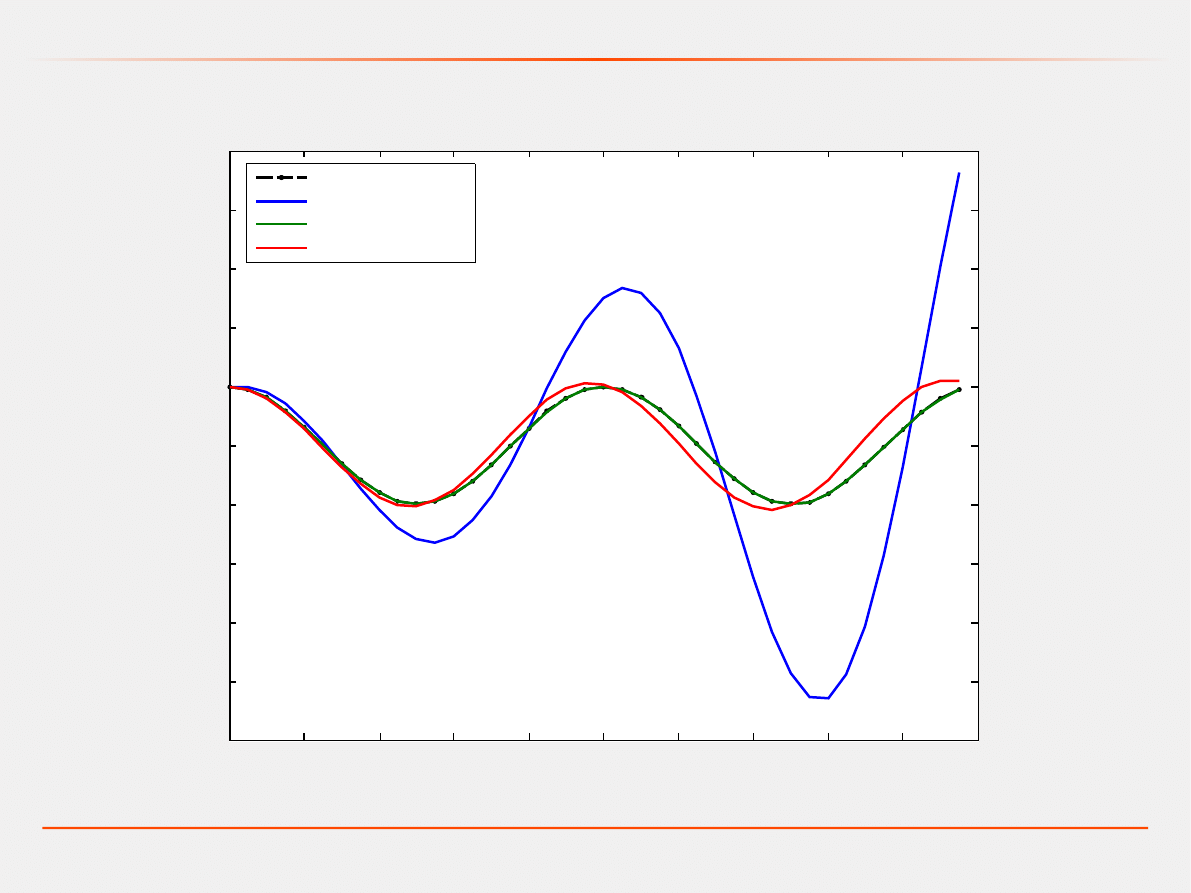
rozwiazanie dokladne
metoda Eulera
metoda Adamsa
metoda RK
¨40⋅=0, h=0.05 , ˙0=0, 0=1
Równanie: