1

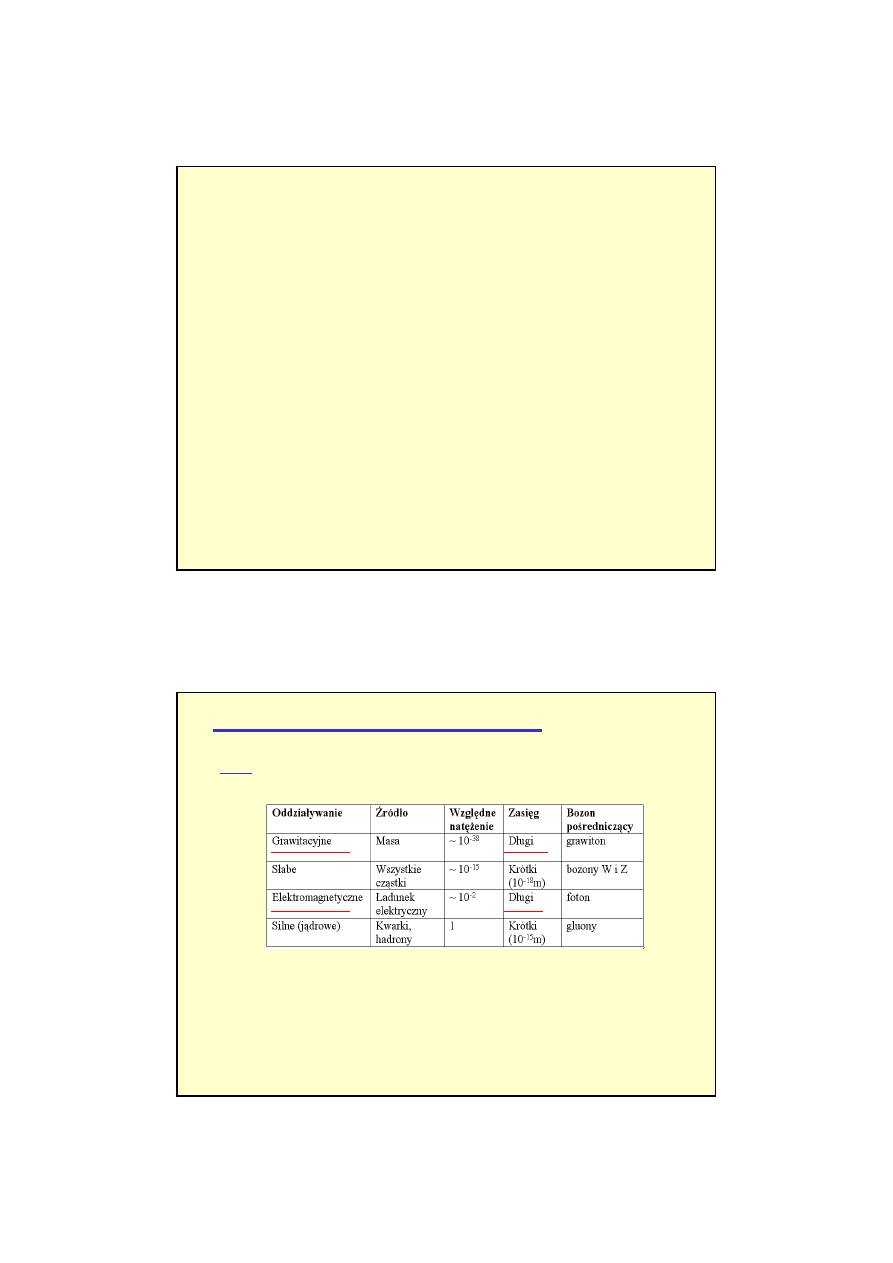
Dynamika

Dynamika w przeciwieństwie do kinematyki zajmuje się
związkiem ruchu z jego przyczyną, tzn. z siłą.

PODSTAWOWE WIELKOŚCI

• Siła jest sposobem opisu oddziaływania ciał.

- Siła ma zdolno

ść

nadawania ciału (ciałom) przyspieszenia, czyli

rozp

ę

dzania ciała.

- Skutkiem działania siły mo

ż

e by

ć

te

ż

deformacja ciała.

- Siła jest wielko

ś

ci

ą

wektorow

ą

:

F

.

2

Masa (bezwładna) jest miar

ą

bezwładno

ś

ci ciała. Ciało o wi

ę

kszej

masie „trudniej” jest rozp

ę

dzi

ć

do pewnej zadanej pr

ę

dko

ś

ci ni

ż

ciało

o masie mniejszej.
„Trudniej” jest te

ż

zatrzyma

ć

ciało o wi

ę

kszej masie, rozp

ę

dzone do

takiej samej pr

ę

dko

ś

ci co ciało o mniejszej masie.

- Definicja przez porównanie:

v

v

0

0

m

m

=

- Inna definicja przez porównanie:

a

a

m

m

0

0

=

Jednostk

ą

masy jest kilogram: 1 kg

wzorzec jest wykonany ze stopu platyny z irydem i
przechowywany w Międzynarodowym Biurze Miar w
Sèvres koło Paryża.

• P

ę

d jest wielko

ś

ci

ą

stosowan

ą

do opisu ciał w ruchu.

Im wi

ę

kszy p

ę

d tym „trudniej” zatrzyma

ć

ciało. Na wielko

ść

p

ę

du

wpływa masa ciała oraz pr

ę

dko

ść

z jak

ą

si

ę

ciało porusza.

Jednostk

ą

p

ę

du jest

Ś

cisła definicja p

ę

du:

v

p

m

=

s

m

kg

3

dt

d

m

dt

m

d

dt

)

d(m

v

v

v

F

+

=

=

2

1

1

s

m

kg

N

=

Jednostk

ą

siły jest:












=

=

=

=

=

const

dla

dt

m

d

const

m

dla

m

dt

d

m

v

v

F

a

v

F

⇒

ZWI

Ą

ZEK MIEDZY PODSTAWOWYMI WIELKO

Ś

CIAMI

t

d

d p

F

=

'

d

)

'

(

)

(

0

0

∫

+

=

t

t

t

t

t

F

p

p

⇒

const

dt

d

dt

d

wyp

=

⇒

=

=

⇒

=

⇒

=

=

∑

v

a

v

p

F

F

0

0

0

Zasada
zachowania p

ę

du

I.

Jeżeli na ciało (o stałej masie) nie działa żadna siła lub

wypadkowa działających sił wynosi zero to ciało porusza się
ruchem jednostajnym prostoliniowym lub pozostaje w
spoczynku.

II.

Jeśli na ciało o stałej masie m działa siła

F

to nadaje ona ciału przyspieszenie

a

,

przy czym związek między tymi wielkościami jest następujący:

a

F

m

=

t

d

d p

F

=

II a. Ogólniejsze prawo mówi, że tempo zmian pędu ciała jest równe sile wypadkowej
działającej na to ciało

ZASADY (PRAWA) DYNAMIKI NEWTONA

1686 –Isaac Newton: „Philosophiae
Naturalis Principia Mathematica”

4

III.

Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na ciało

pierwsze jest równa i przeciwnie skierowana do siły, jaką ciało pierwsze działa na
drugie (siła akcji równa jest sile reakcji).

F

akcji

F

reakcji

a)

B

A

F

AB

F

BA

b)

Reakcja na nacisk

* Ścisła definicja układu inercjalnego: jest to taki układ, w którym spełnione
są zasady dynamiki Newtona.

UWAGI:

* Mechanika klasyczna (newtonowska) jest szczególnym przypadkiem
ogólniejszych teorii:

Mechanika

kwantowa

Sczególna

teoria względnosci

Mechanika

klasyczna

c

v

<<

o

A

1

>>

l

BA

AB

F

F

−

=

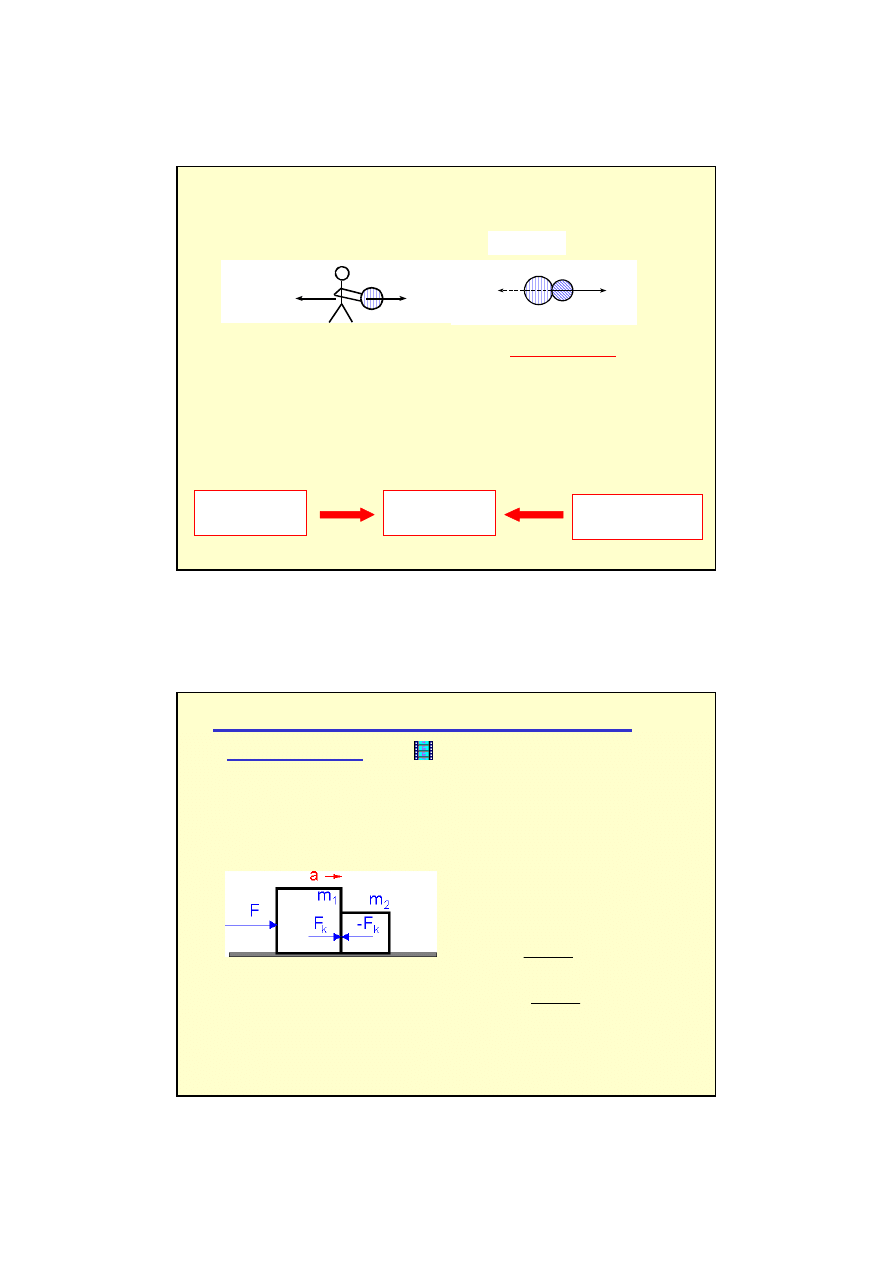
Siły kontaktowe

Gdy dwa ciała są dociskane do siebie to występują między nimi

siły kontaktowe

.

PRZYKŁADY SIŁ RZECZYWISTYCH

Źródłem tych sił jest odpychanie pomiędzy atomami, jest to siła elektromagnetyczna.

a

a

F

1

2

m

m

=

−

Siła kontaktowa

F

k

to siła z jaką klocek o masie m

1

działa na klocek o masie m

2

nadając mu przyspieszenie.







=

=

−

a

F

a

F

F

2

1

m

m

k

k













+

=

+

=

F

F

F

a

2

1

2

2

1

m

m

m

m

m

k

5

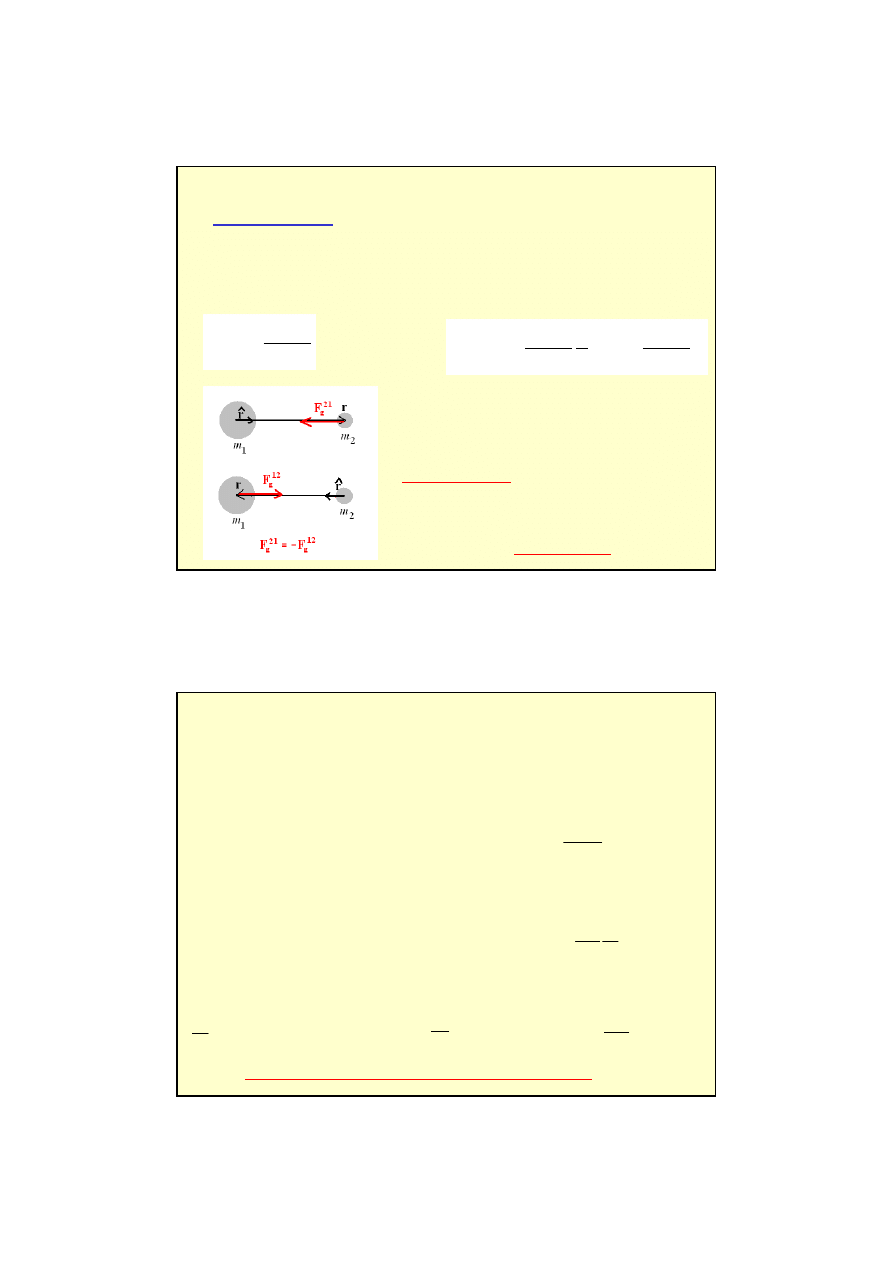
Każde dwa ciała o masach m

1

i m

2

przyciągają się wzajemnie siłą grawitacji wprost

proporcjonalną do iloczynu mas, a odwrotnie proporcjonalną do kwadratu odległości
między nimi.

2

2

1

r

m

m

G

F

=

r

r

F

ˆ

2

2

1

2

2

1

r

m

m

G

r

r

m

m

G

g

−

=

−

=

lub wektorowo

Masy m

1

i m

2

występującą we powyższym wzorze

nazywamy masami grawitacyjnymi.

Siła grawitacji

Masa występująca w II zasadzie dynamiki
Newtona ( F=ma) to masa bezwładna.

Masa grawitacyjna jest źródłem oddziaływania
grawitacyjnego.

Siła grawitacji – masa grawitacyjna i bezwładna

Czy masa bezwładna i masa grawitacyjna ciała są sobie równe ???

Obliczamy przyspieszenia jakie uzyskuje masa

m (bezwładna)

spadająca swobodnie w

pobliżu powierzchni Ziemi.

ma

Q

=

II zasada dynamiki Newtona mówi, że:

m

m

R

M

G

a

Z

Z

'

2

=

Obliczamy przyspieszenie:

Masa grawitacyjna i bezwładna są sobie równe !!!

Doświadczalnie stwierdzono, że wszystkie ciała spadają (w próżni) w pobliżu Ziemi z tym
samym przyspieszeniem a = g.

const

m

m

=

'

dobierzmy G tak aby:

1

'

=

m

m

wtedy:

2

Z

Z

R

M

G

g

=

2

'

Z

Z

R

M

m

G

Q

=

Na masę

m’ (grawitacyjną)

działa siła ciężkości:

6

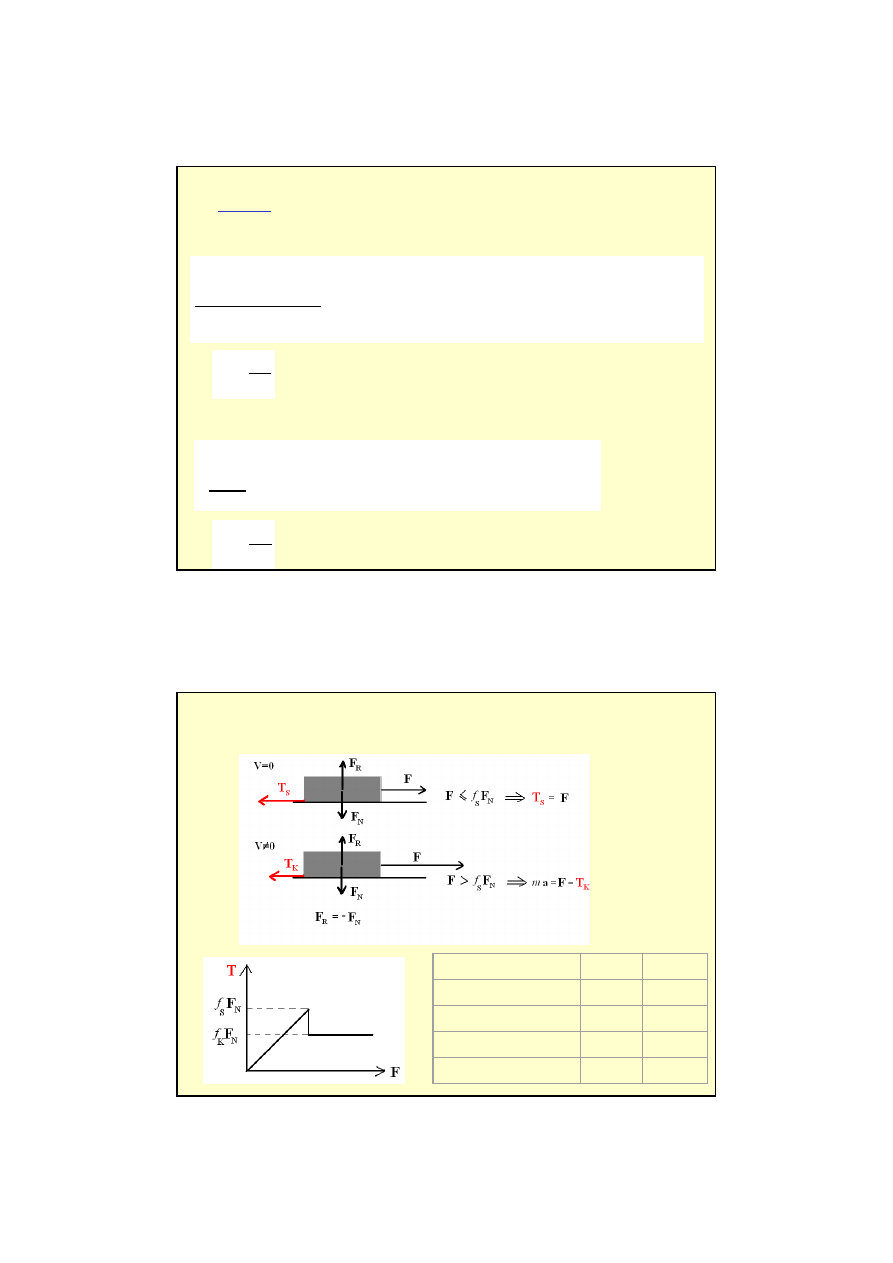
Siła tarcia zawsze działa stycznie do powierzchni zetknięcia ciał

• Siłę tarcia działającą między nieruchomymi powierzchniami nazywamy

tarciem statycznym T

s

Prawa dotyczące tarcia:
- T

s

jest w przybliżeniu niezależna od wielkości pola powierzchni styku ciał,

- T

s

jest proporcjonalna do siły z jaką jedna powierzchnia naciska na drugą.

N

s

s

F

T

f

=

Stosunek maksymalnej siły T

s

do siły nacisku F

N

nazywamy

współczynnikiem tarcia statycznego f

s

Tarcie

Stosunek siły T

k

do siły nacisku F

N

nazywamy

współczynnikiem tarcia kinetycznego f

k

• Gdy ciało porusza się, to mamy do czynienia z siłą

tarcia kinetycznego T

k

Prawo:
T

k

nie zależy od prędkości względnej poruszania się powierzchni.

N

k

k

F

T

f

=

Tarcie – przykład 1

Rodzaj powierzchni

f

s

f

k

Stal po stali

0.15

0.03- 0.09

Drewno po drewnie

0.54

0.34

Drewno po kamieniu

0.7

0.3

Stal po lodzie (np. łyżwy)

0.027

0.014

7

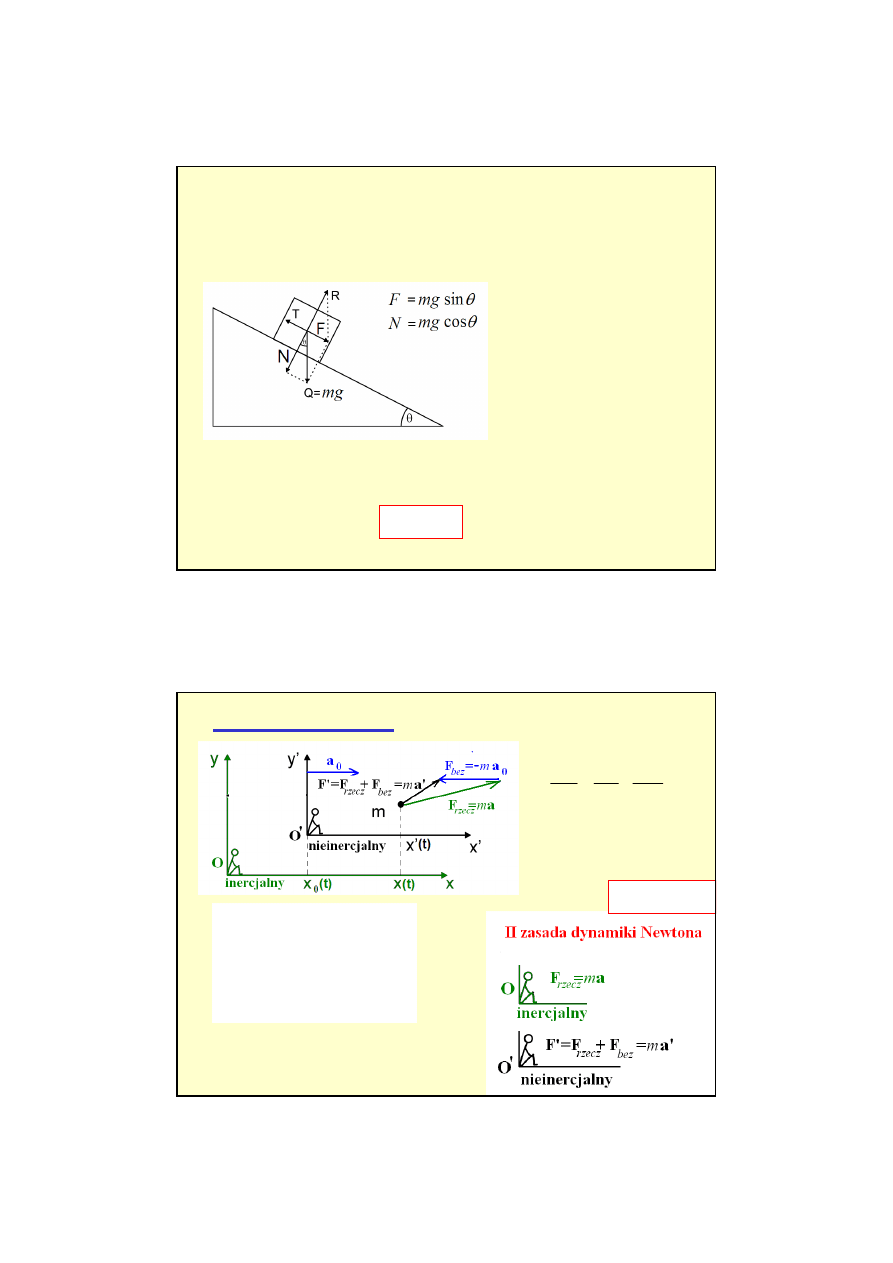
Tarcie – przykład 2

Ciało o masie m spoczywa na równi pochyłej, której kąt nachylenia θ stopniowo zwiększamy.
Przy jakim granicznym kącie nachylenia ciało zacznie się zsuwać jeżeli współczynnik
tarcia statycznego klocka o równię wynosi f

s

?

θ

cos

Q

f

T

s

=







=

=

θ

θ

cos

sin

Q

N

Q

F

θ

tg

f

s

<

θ

θ

sin

cos

Q

Q

f

F

T

s

<

⇒

<

ciało zsuwa się

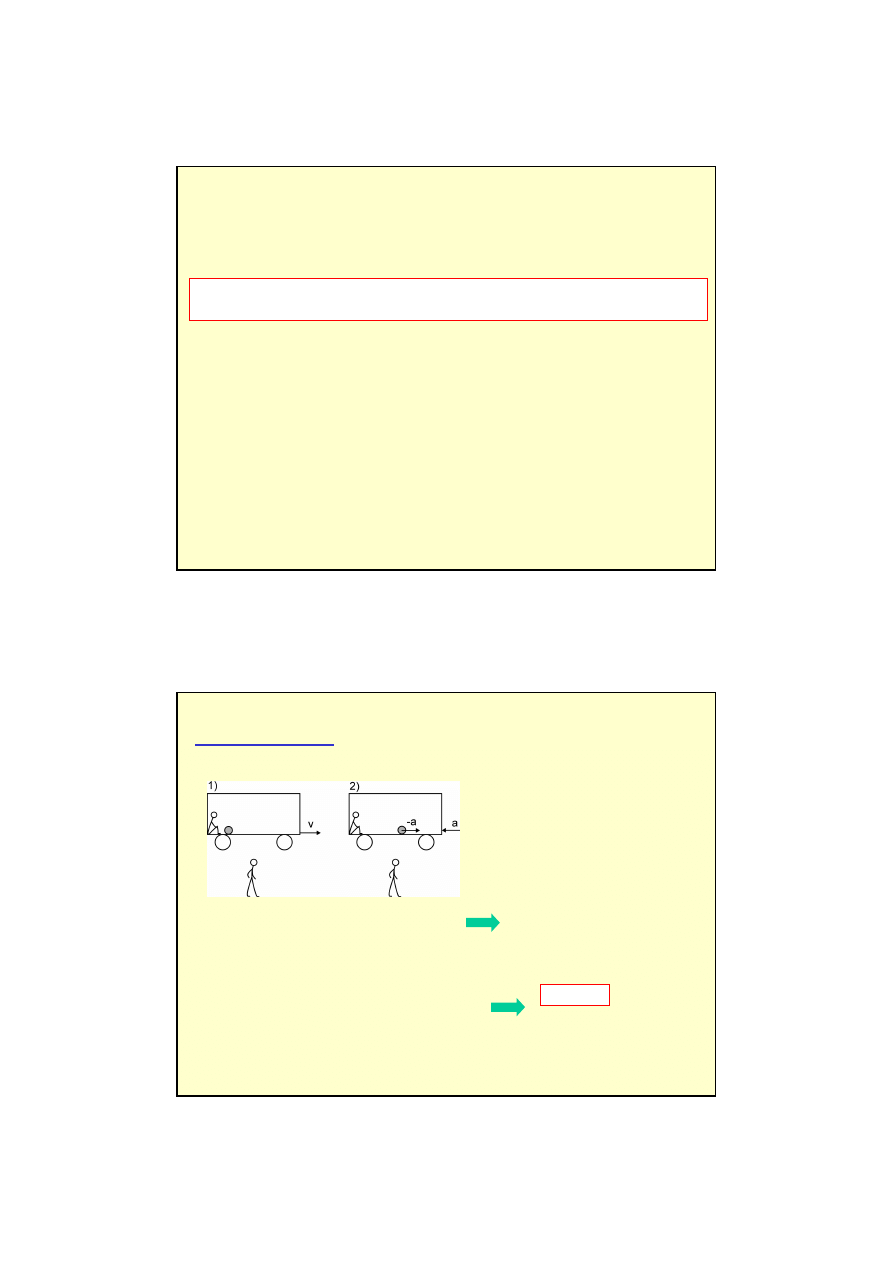
SIŁY POZORNE

0

bez

a

F

m

−

=

)

(

)

(

)

(

'

0

t

x

t

x

t

x

−

=

0

'

a

a

a

−

=

2

0

2

2

2

2

2

'

t

d

x

d

t

d

x

d

t

d

x

d

−

=

bez

rzecz

0

0

F

F

a'

a

a

a'

a

a

a'

+

=

−

+

=

−

=

m

m

m

m

)

(

Iloczyn masy i przyspieszenia
unoszenia (ze znakiem minus)
nazywamy siłą bezwładności F

bez

.

8

Uzupełnienie definicji układu inercjalnego: jest to taki układ, w którym spełnione są
zasady dynamiki Newtona i nie istnieją siły pozorne.

• Układy inercjalne poruszają się względem siebie ruchem jednostajnym
prostoliniowym lub pozostają w spoczynku.

• W układach inercjalnych ruchem ciał rządzą dokładnie te sama prawa.

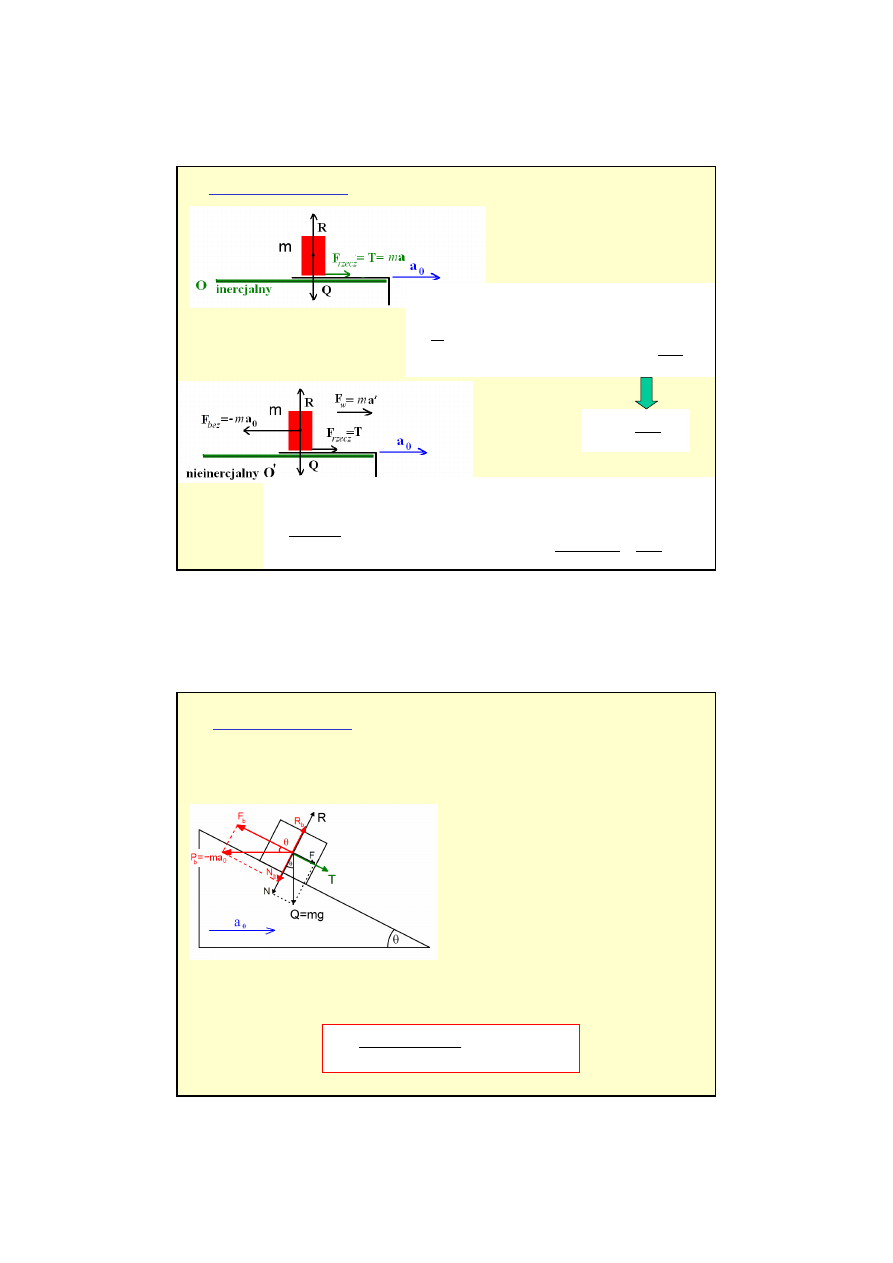
Ruch prostoliniowy

- dwaj obserwatorzy opisuj

ą

ruch kulki znajduj

ą

cej si

ę

w samochodzie

jeden z obserwatorów stoi na Ziemi,
a drugi znajduje się w samochodzie,

samochód jedzie ze stałą prędkością (rys. 1)

v

kulki

= 0 ⇒

⇒

⇒

⇒ F = 0

(O’ )

v

kulki

= v = const. ⇒

⇒

⇒

⇒ F = 0

(O)

(obserwatorzy O i O’ znajdują się w inercjalnych układach odniesienia)

samochód hamuje ze stałym opóźnieniem a (rys. 2),

(między kulką, a podłogą samochodu nie ma tarcia)

a

F

kulki

m

−

=

(O’)

(obserwator O’ znajduje się w układzie nieinercjalnym a obserwator O jest w układzie inercjalnym)

v

kulki

= v = const. ⇒

⇒

⇒

⇒ F = 0 (O)

O

O

O’

O’

9











<

=

⇒

=

⇒

>

=

⇒

=

⇒

≤

⇒

=

=

0

0

0

0

0

a

m

Q

f

a

Q

f

T

Q

f

ma

a

a

ma

T

Q

f

ma

m

m

T

a

a

T











<

−

=

−

=

⇒

=

⇒

>

=

⇒

=

⇒

≤

⇒

−

=

−

=

=

+

0

'

0

'

'

'

0

0

0

0

0

0

0

a

m

Q

f

m

ma

Q

f

a

Q

f

T

Q

f

ma

a

ma

T

Q

f

ma

m

m

m

m

a

T

a

a

F

a

F

T

bez

bez

0

0

a

m

Q

f

a

a

−

=

−

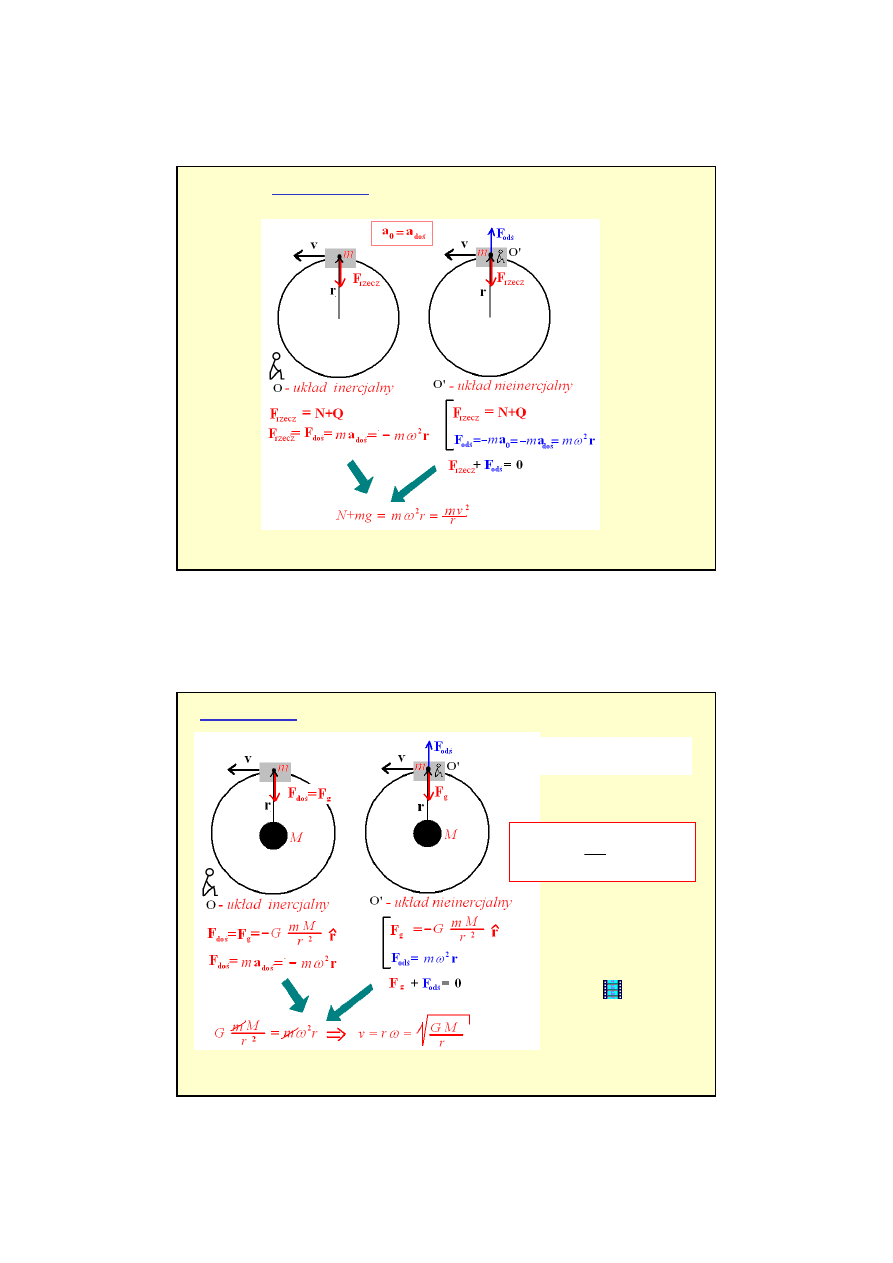
Ruch prostoliniowy

- wyrywanie obrusu

Z jakim przyspieszeniem poziomym powinna poruszać się w kierunku poziomym równia aby
ciało zaczęło się po niej wsuwać do góry ?







=

=

θ

θ

sin

cos

0

0

ma

N

ma

F

b

b

)

cos

sin

(

0

max

θ

θ

mg

ma

f

T

s

+

=







=

=

θ

θ

cos

sin

mg

N

mg

F

)

cos

sin

sin

cos

0

0

θ

θ

θ

θ

mg

(ma

f

mg

ma

s

+

>

−

ctgθ

f

g

θ

f

θ

θ

θ

f

a

s

s

s

<

−

+

>

i

sin

cos

sin

cos

0

Ruch prostoliniowy

– tarcie i bezwładność

10

Siła odśrodkowa

- kamień na sznurku

Siła odśrodkowa

– stan nieważkości

r

r

F

odś

2

2

ˆ

ω

m

r

v

m

=

=

jeden z obserwatorów (O) stoi na Ziemi,
a drugi znajduje się w sputniku (O’)

11

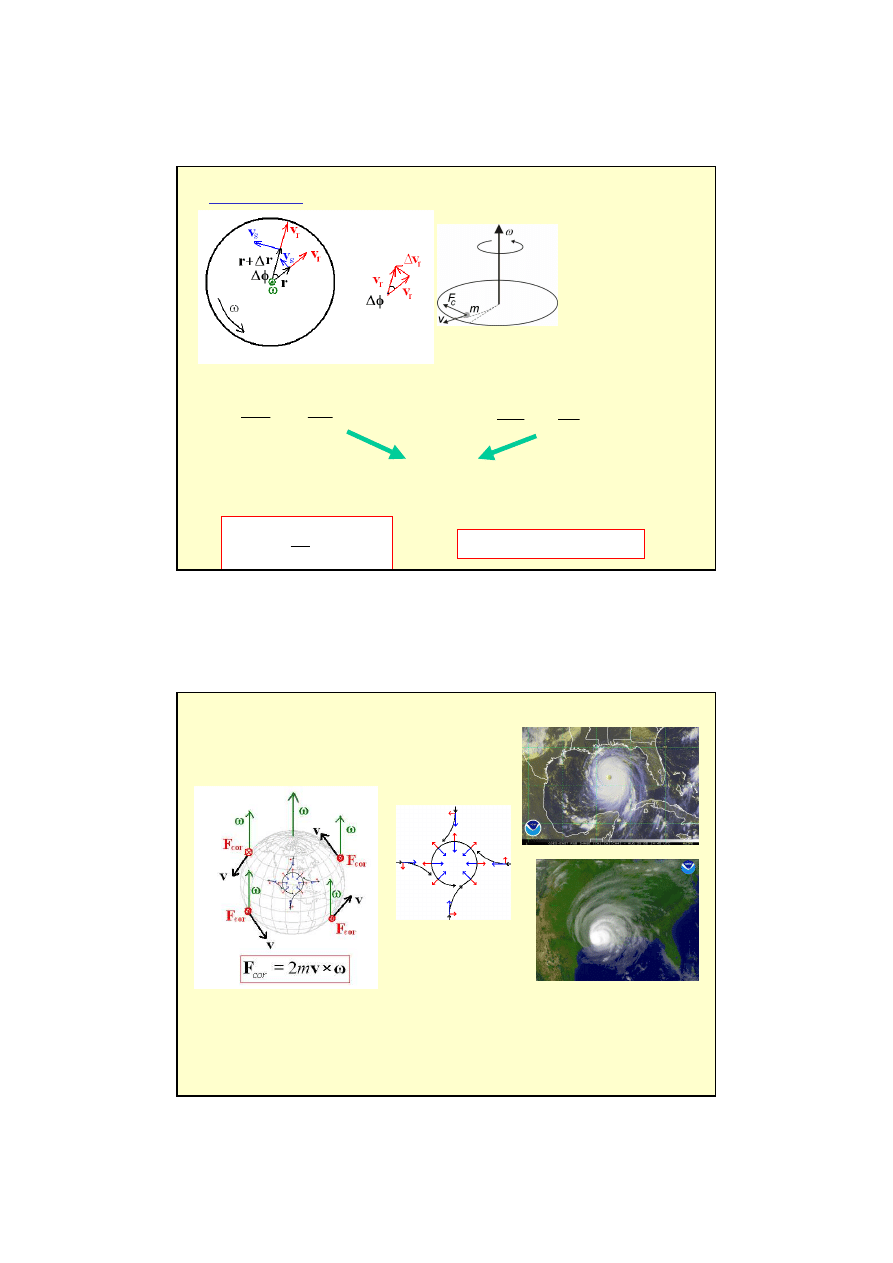
Biedronka porusza się wzdłuż
promienia tarczy ze stałą prędkością v

r

(względem tarczy !!)

Obserwator w układzie
inercjalnym
(zewnętrznym) widzi
przyspieszenia:

a

1

- zmieniające kierunek

prędkości v

r

,

a

2

- zwiększające

prędkość styczną v

s

.

φ

∆

=

∆

r

r

v

v

Siła Coriolisa

r

r

F

odś

2

2

ˆ

ω

m

r

v

m

=

=

ω

v

a

F

cor

cor

×

=

−

=

m

m

2

Siły bezwładno

ś

ci działaj

ą

ce w układzie obracaj

ą

cym si

ę

:

r

s

2

d

d

d

d

v

t

r

t

v

a

ω

ω

=

=

=

r

r

r

r

v

∆

=

−

∆

+

=

∆

ω

ω

ω

)

(

)

(

s

ω

φ

r

r

r

1

d

d

d

v

t

d

v

t

v

a

=

=

=

ω

r

cor

v

a

a

a

a

2

2

1

0

=

+

=

=

przyspieszenie Coriolisa

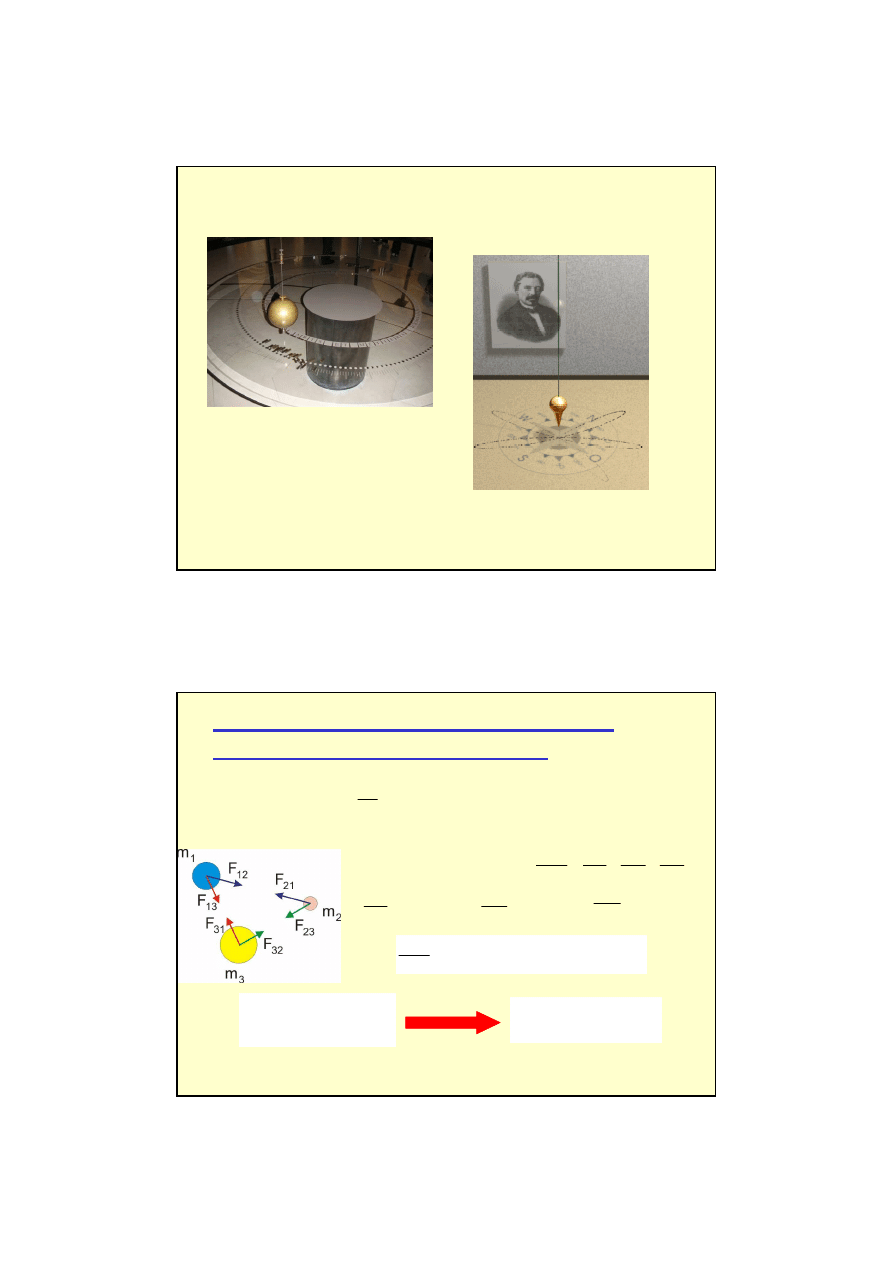
Mieszkamy na Ziemi – wirującej planecie

Ruch obrotowy Ziemi powoduje zmianę kierunku poruszających się po jej powierzchni ciał.
• silniejsze podmywanie prawych brzegów rzek na półkuli północnej i lewych na

półkuli południowej

• odchylenie kierunków wiatrów stałych
• układ prądów morskich
• odchylenie toru ciał spadających

RITA 2005

KATRINA 2005

Siła Coriolisa

na Ziemi

12

Siła Coriolisa

- wahadło Foucaulta

Wahadło Foucaulta w Muzeum Sztuk i Rzemiosł
w Paryżu; w miarę obrotu wahadło przewraca
ustawione wokoło klocki.

Wahadło Foucaulta - Kościół św. Piotra i Pawła w Krakowie: 46,5m , 25 kg

ZASADY DYNAMIKI DLA UKŁADU
PUNKTÓW MATERIALNYCH

Jeżeli wypadkowa sił zewnętrznych działających na układ jest równa
zeru, to całkowity wektor pędu układu pozostaje stały.

const

=

cał

p

0

.

=

∑

zewn

F

const

dt

d

wyp

=

⇒

=

⇒

=

=

∑

p

p

F

F

0

0

Punkt materialny:

3

2

1

p

p

p

p

cał

+

+

=

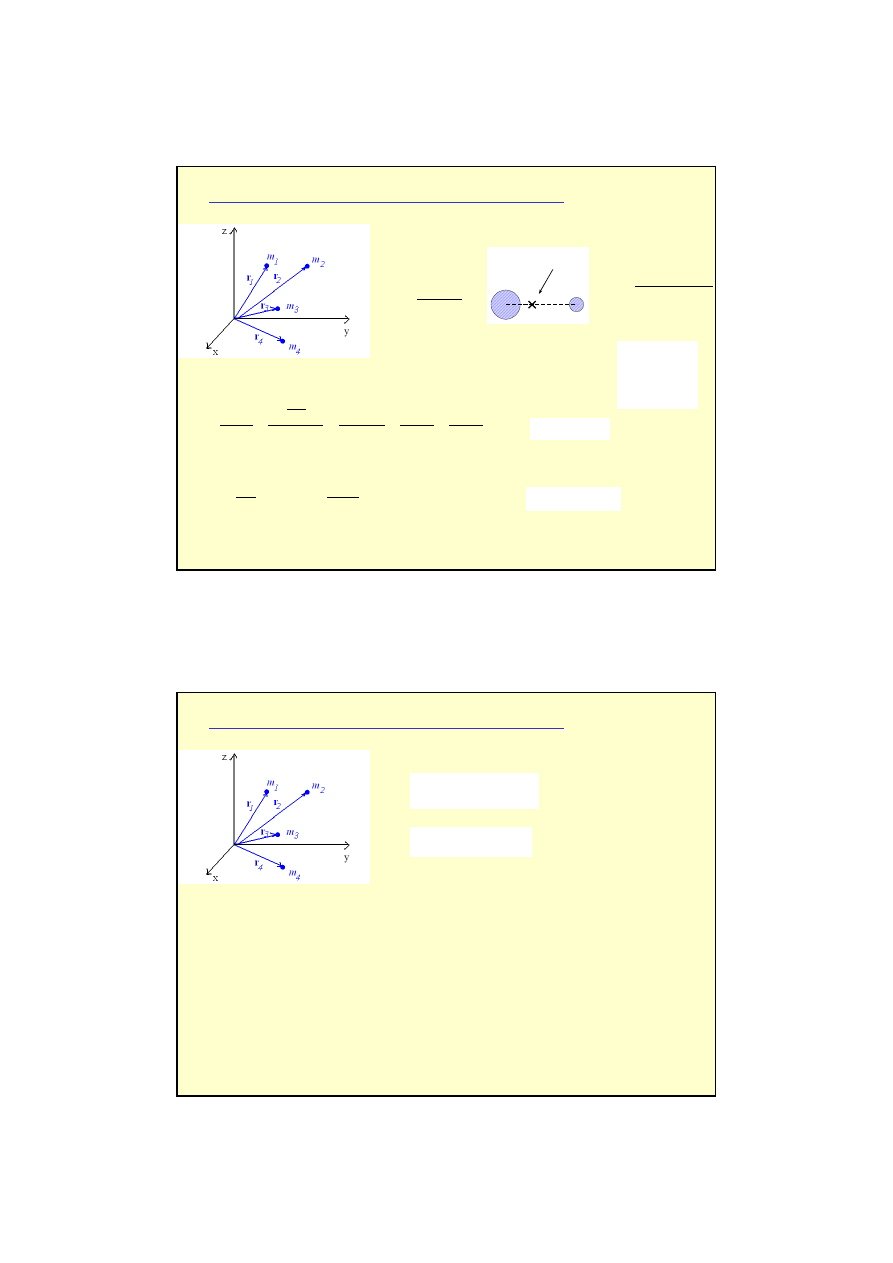
13

12

1

F

F

p

+

=

dt

d

23

21

2

F

F

p

+

=

dt

d

32

31

3

F

F

p

+

=

dt

d

dt

d

dt

d

dt

d

dt

d

3

2

1

p

p

p

p

cał

+

+

=

0

32

23

31

13

21

12

=

+

+

+

+

+

=

F

F

F

F

F

F

p

cał

dt

d

Układ punktów materialnych:

13

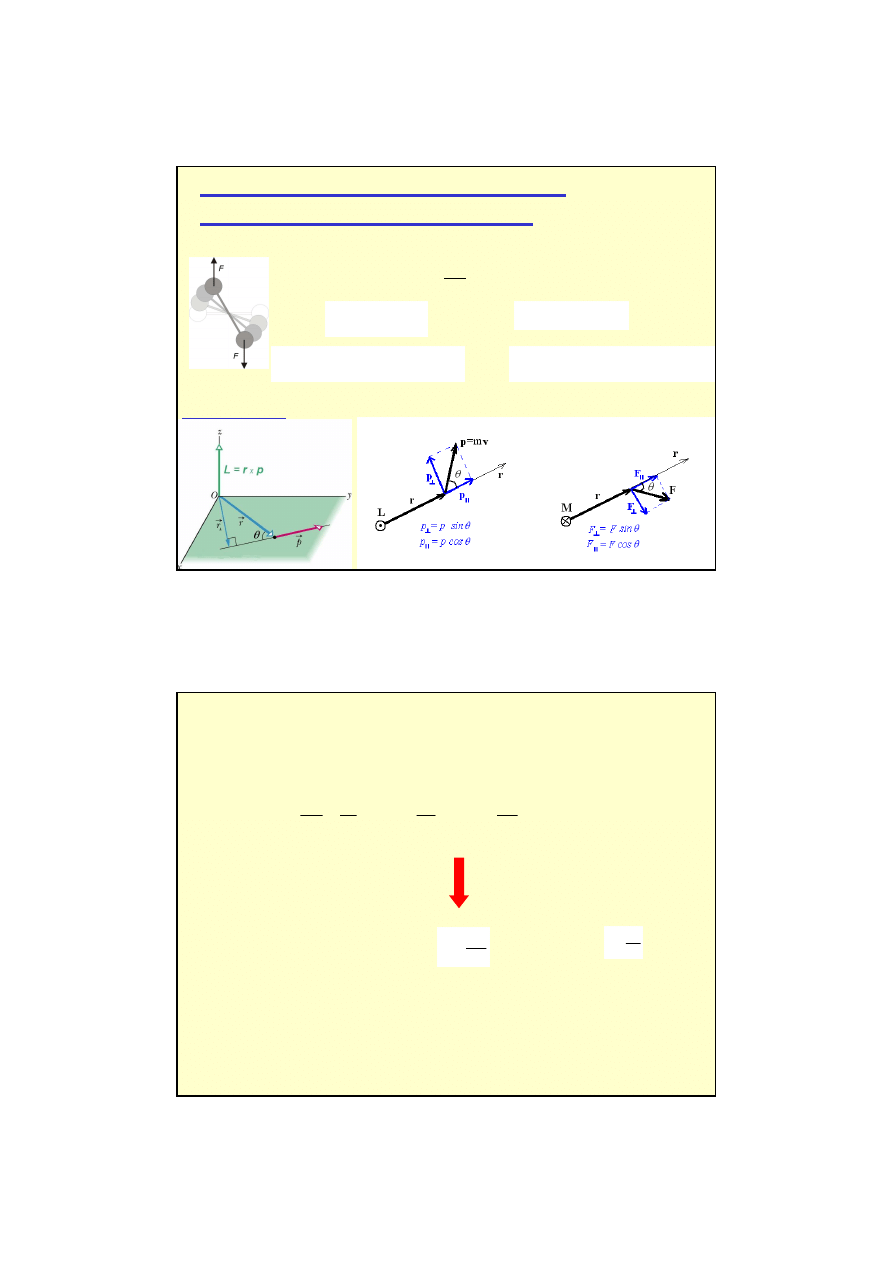
Ś

rodek masy – zasady dynamiki Newtona

m

m

=

i

N

=1

i

i

N

=1

i

∑

∑

r

R

i

sm

m

+

m

m

+

m

=

2

1

2

1

r

r

R

2

1

sm

ś

rodek masy

∑

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

=

=

=

=

=

=

N

i

i

N

i

i

N

i

N

i

i

N

i

i

N

i

i

N

i

i

m

m

m

m

m

m

dt

dt

d

1

1

1

1

1

1

1

d

ca ł

i

i

i

sm

sm

p

p

v

r

R

V

sm

sm

a

V

F

P

M

dt

d

M

dt

d

zew

=

=

=

⇒

sm

a

F

M

zew

=

siła zewnętrzna powoduje przyspieszenie sm

⇒

∑

=

=

N

i

i

m

M

1

oznaczmy:

sm

V

P

M

=

całkowity pęd = pęd sm

cał

p

P

=

Opis układu wielu ciał staje się bardzo prosty i sprowadza się
formalnie do takich samych wzorów jak dla pojedynczej cząstki pod
warunkiem, że zastąpimy prędkość, pęd i przyspieszenie cząstki
przez te same wielkości, ale odniesione do środka masy.

∑

=

=

N

i

i

m

M

1

M

sm

V

P

=

sm

a

F

M

zew

=

Ś

rodek masy – zasady dynamiki Newtona

0

P

p

V

v

V

(v

p

i

sm

i

sm

i

sm
i

=

−

=

−

=

−

=

∑

∑

∑

∑

∑

=

=

=

=

=

N

i

N

i

N

i

i

i

N

i

N

i

i

m

m

m

1

1

1

1

1

)

Suma pędów cząstek względem środka masy wynosi 0 !!

∑

=

N

i 1

sm
i

p

14

Pomimo, że siła wypadkowa = 0 to ciało może być wprawione w ruch - obrót

ZASADY DYNAMIKI NEWTONA
DLA RUCHU OBROTOWEGO

0

=

wyp

F

0

d

d

=

t

p

0

=

a

p

r

L

×

=

⊥

=

=

p

r

p

r

L

θ

sin

Wielkościami, używaną do opisu ruchu obrotowego są:
moment pędu L (analogiczny do pędu) i moment siły M (analogiczny do siły)

F

r

M

×

=

⊥

=

=

F

r

F

r

M

θ

sin

(

)

F

r

p

v

p

r

p

r

p

r

L

×

+

×

=

×

+

×

=

×

=

t

d

d

t

d

d

t

d

d

t

d

d

0

=

×

⇒

p

v

p

v

II

t

d

dL

M

=

Zmiana pędu w czasie jest równa sile (F), a zmiana momentu pędu w czasie
momentowi siły (M).

t

d

dp

F

=

II zas. dynamiki Newtona:

Druga zasada dynamiki dla ruchu obrotowego:

15

STATYKA: Aby ciało było w równowadze suma sił zewnętrznych i momentów sił

zewnętrznych musi być równa zeru

const.

t

wyp

=

⇒

=

⇒

=

p

p

F

0

d

d

0

Zasada zachowania pędu :

const.

t

wyp

=

⇒

=

⇒

=

L

L

M

0

d

d

0

Zasada zachowania momentu pędu :

ZASADY ZACHOWANIA:
PĘDU I MOMENTU PĘDU

Punkt materialny:

Układ punktów materialnych:

const.

t

=

⇒

=

⇒

=

∑

cał

cał

zew

p

p

F

0

d

d

0

Zasada zachowania pędu :

const.

t

=

⇒

=

⇒

=

∑

cał

cał

zew

L

L

M

0

d

d

0

Zasada zachowania momentu pędu :

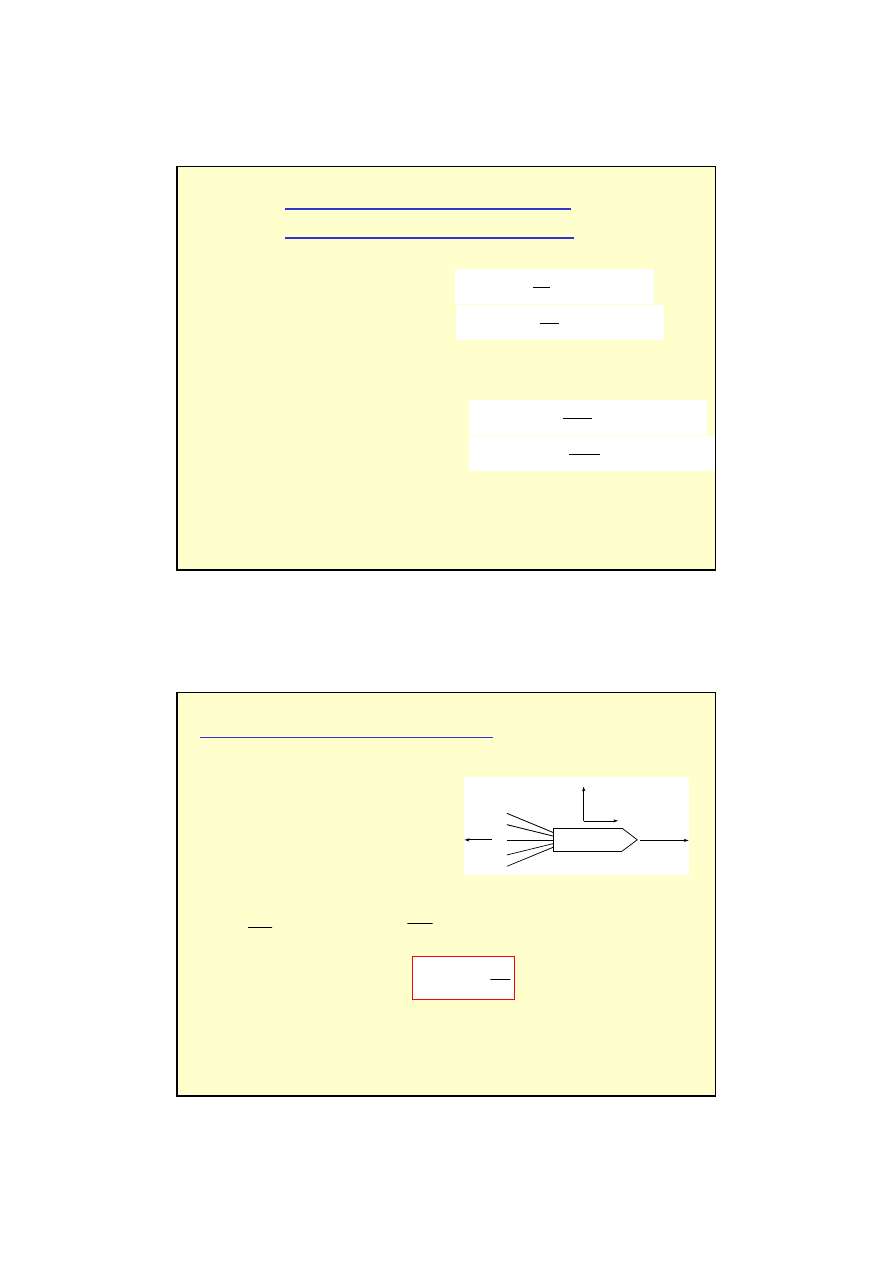
Przykład zasady zachowania p

ę

du

-

napęd odrzutowy (ruch rakiety)

x

u

m

y

v

)

( gazów

dm

u

dv

m

=

W układzie zwi

ą

zanym z rakiet

ą

:

dm

u

dv

m

−

=

ponieważ masa rakiety zmniejsza się o

)

( gazów

dm

dm

−

=

m

dm

u

dv

−

=

⇒

[ ]

m

m

v

v

m

m

o

o

o

m

u

m

dm

u

dv

∫

∫

−

=

−

=

'

ln

'

'

'

Jaki musi być stosunek masy początkowej do końcowej m

o

/m rakiety, aby osiągnęła ona

pierwszą prędkość kosmiczną (v = 7.9 km/s) ? Przyjąć typową prędkość wyrzucanych gazów:
u= 3 km/s.
Odp. m

o

/m = 14

)

ln

(ln

o

o

m

m

u

v

v

−

−

=

−

m

m

u

v

v

o

o

ln

+

=

Wzór Ciołkowskiego

⇒

16

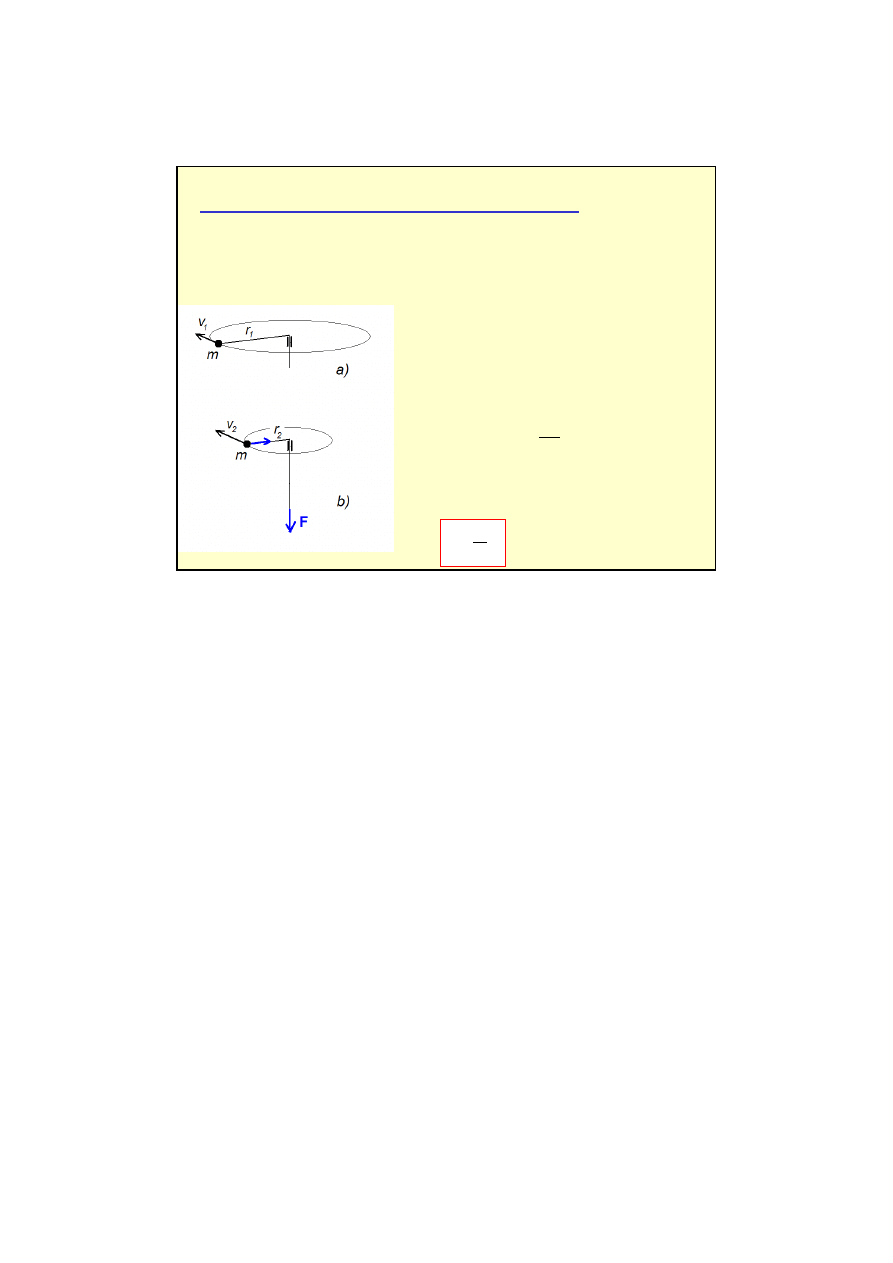
Przykład zasady zachowania momentu p

ę

du

Ciało o masie m porusza się w płaszczyźnie poziomej po okręgu o promieniu r

1

(a). Prędkość

liniowa ciała wynosi v

1

. Ile razy zmieni się prędkość liniowa ciała, jeśli pociągając za sznurek

jak na rys (b) zmniejszymy promień okręgu do długości r

2

(b) . Zakładamy, że nie działa siła

grawitacji.

a)

1

1

v

r

m

L

m

=

=

1

1

v

r

L

x

1

1

v

r

⊥

const.

0

d

d

0

=

⇒

=

⇒

=

=

L

L

F

r

M

1

t

x

b)

siła F działa wzdłuż sznurka i zawsze prostopadle

do prędkości ciała , czyli:

F

r

1

||

2

2

1

1

v

r

m

v

r

m

L

=

=

1

2

1

2

v

r

r

v

=