KONSPEKT LEKCJI MATEMATYKI

Autor:

Klasa: II liceum (matematyczna)

Dział tematyczny: Wielomiany

Temat: Rozkład wielomianu na czynniki. Najmniejsza wspólna wielokrotność

i największy wspólny dzielnik wielomianów.

Program: Matematyka z plusem

Baza:
- Uczeń zna pojęcie wielomianu jednej zmiennej;
- Uczeń zna pojęcie pierwiastka wielomianu;
- Uczeń zna twierdzenie Bezout;
- Uczen zna i umie stosować schemat Hornera;
- Uczeń zna twierdzenia o całkowitych i wymiernych pierwiastkach wielomianu;
- Uczeń wie, że każdy wielomian można rozłożyć na czynniki stopnia co najwyżej drugiego;
- Uczeń zna wzory skróconego mnożenia;
- Uczeń potrafi rozkładać wielomiany na czynniki wyłączając wspólny czynnik przed nawias,
wykorzystując wzory skróconego mnożenia bądź grupując wyrazy;
- Uczeń zna pojęcie największego wspólnego dzielnika i najmniejszej wspólnej wielokrot-
ności kilku liczb naturalnych.

Cele:
- Uczeń potrafi rozkładać wielomian na czynniki stosując różne metody;
- Uczeń potrafi wyznaczać największy wspólny dzielnik i najmniejszą wspólną wielokrot-
ność kilku wielomianów.

Metody:
- Podająca (podanie metod rozwiązań przykładów, których uczniowie nie potrafią samodziel-
nie rozwiązać, podanie definicji NWD i NWW wielomianów);
- Poszukująca (odpowiadanie przez uczniów na pytania pojawiające się w trakcie rozwiązy-
wania zadań);
- Praktyczna (liczenie zadań).

Zasady:
- Trwałości wiedzy (zadanie pracy domowej);
- Świadomego i aktywnego udziału ucznia w procesie nauczania i uczenia się (samodzielne
rozwiązywanie zadań, próby rozwiązania pojawiających się problemów);
- Przystępności (dobór zadań według możliwości uczniów; stopniowanie trudności zadań);
- Systematyczności (wykorzystanie znanych pojęć (np. całkowitych i wymiernych pier-
wiastków wielomianu, czy NWD i NWW liczb naturalnych) do wprowadzenia nowych
pojęć lub rozwiązywania nowych problemów).

1

Czynności wstępne:

Witam się z uczniami i sprawdzam obecność.
Mówię uczniom, że będziemy kontunuować temat z poprzedniej lekcji, czyli „Rozkład
wielomianu na czynniki.”
Nie sprawdzam zadania domowego, ponieważ dla uczniów jest to druga lekcja tego dnia.
Ja kontynuuję temat.

Część wprowadzająca:

Jeśli nie musimy dokończyć przykładów z poprzedniej lekcji, przechodzimy do zadania
następnego:

Zad. 3.67
Rozłóż na czynniki wielomiany:
a) W (x) = x

4

+ 1

Pytam uczniów, czy ten wielomian da rozłożyć się na czynniki. Może się zdarzyć, że
uczniowie odpowiedzą, że nie i będą argumentować swoją odpowiedź tym, że dla wszyst-
kich liczb wielomian ten przyjmuje wartości dodatnie. Tłumaczę wtedy, że to powoduje
brak pierwiastków tego wielomianu, ale nie brak możliwości rozkładu tego wielomianu na
czynniki. Przypominam uczniom, że każdy wielomian da się rozłożyć na czynniki stopnia
co najwyżej drugiego, a ten wielomian ma stopień 4, czyli na pewno da się go rozłożyć.
Zaznaczam jednak, że powyższa argumentacja uczniów jest poprawna dla wielomianów
stopnia 2.

Do rozwiązania przykładu proszę ucznia. Jeśli uczeń nie ma pomysłu na rozwiązanie,
proszę o podpowiedź resztę uczniów. W ostateczności podpowiadam sama, że należy do-
dać i odjąć 2x

2

, a następnie skorzystać z odpowiednich wzorów skróconego mnożenia.

Rozwiązanie:
W (x) = x

4

+ 1 = x

4

+ 2x

2

− 2x

2

+ 1 = x

4

+ 2x

2

+ 1 − 2x

2

= (x

2

)

2

+ 2 · x

2

· 1 + 1

2

− 2x

2

=

(x

2

+1)

2

−(

√

2x)

2

= (x

2

+1+

√

2x)(x

2

+1+

√

2x)(x

2

+1−

√

2x) = (x

2

+

√

2x+1)(x

2

−

√

2x+1)

Pytam uczniów, czy nie da się rozłożyć jeszcze tych czynników, które otrzymaliśmy. Do-
chodzimy do wniosku, że nie, bo wyróżnik obydwu jest ujemny:
∆ = (

√

2)

2

− 4 · 1 · 1 = 2 − 4 = −2

Zapisujemy pod odpowiednimi nawiasami: ∆ < 0

b) W (x) = x

4

+ 9

Mówię uczniom, że przykład ten jest podobny do poprzedniego, trzeba jednak dodać i
odjąć inny jednomian. Uczniowie sami mają zaproponować jaki to ma być jednomian.
Jeśli uczniowie bez problemu odpowiedzą oraz sprawnie policzą poprzedni przykład, to ten
przykład będą mieli dokończyć w domu. Jeśli jednak pojawią się problemy rozwiążemy go
wspólnie na lekcji.

2

Rozwiązanie:
W (x) = x

4

+ 9 = x

4

+ 6x

2

− 6x

2

+ 9 = x

4

+ 6x

2

+ 9 − 6x

2

= (x

2

)

2

+ 2 · x

2

· 3 + 3

2

− 6x

2

=

(x

2

+ 3)

2

− (

√

6x)

2

= (x

2

+ 3 +

√

6x)(x

2

+ 3 −

√

6x) = (x

2

+

√

6x + 3)(x

2

−

√

6x + 3)

Tak jak poprzednio pytam uczniów, czy można rozłożyć otrzymane czynniki. Wspólnie
dochodzimy do wniosku, że nie, bo wyróżniki są ujemne:
∆ = (

√

6)

2

− 4 · 1 · 3 = 6 − 12 = −6

Zapisujemy pod odpowiednimi nawiasami: ∆ < 0

c) W (x) = 2x

4

+ 32

Pytam uczniów o pomysł na rozwiązanie. W ostateczności odpowiadam, że najpierw należy
wyłączyć 2 przed nawias, a dalej rozwiązywać podobnie do poprzednich przykładów.

Rozwiązanie:
W (x) = 2x

4

+ 32 = 2[x

4

+ 16] = 2[x

4

+ 8x

2

− 8x

2

+ 16] = 2[x

4

+ 8x

2

+ 16 − 8x

2

] =

2[(x

2

)

2

+ 2 · x

2

· 4 + 4

2

− 8x

2

] = 2[(x

2

+ 4)

2

− (

√

8x)

2

] = 2(x

2

+ 4 +

√

8x)(x

2

+ 4 −

√

8x) =

2(x

2

+ 2

√

2x + 4)(x

2

− 2

√

2x + 4)

Ponownie pytam uczniow, czy można rozłożyć otrzymane czynniki. Wspólnie dochodz-
imy do wniosku, że nie, bo wyróżniki są ujemne:
∆ = (2

√

2)

2

− 4 · 1 · 4 = 8 − 16 = −8

Zapisujemy pod odpowiednimi nawiasami: ∆ < 0

Następnie przechodzimy do kolejnego zadania:
Zad. 3.68
Rozłóż na czynniki wielomiany:
a) W (x) = x

6

− 1

Jeśli uczeń nie ma pomysłu na rozwiązanie, proszę o podpowiedź resztę uczniów. W os-
tateczności podpowiadam sama, że można zapisać ten wielomian inaczej:
W (x) = (x

2

)

3

− 1

3

i dalej skorzystać ze wzoru skróconego mnożenia.

Rozwiązanie:
W (x) = (x

2

)

3

− 1

3

= (x

2

− 1)((x

2

)

2

+ x

2

· 1 + 1

2

) = (x − 1)(x + 1)(x

4

+ x

2

+ 1)

Jeżeli uczeń nie potrafi rozłożyć na czynniki wielomianu x

4

+ x

2

+ 1 podpowiadam, że x

2

można zapisać jako 2x

2

− x

2

i skorzystać dalej ze wzoru skróconego mnożenia:

W (x) = (x − 1)(x + 1)(x

4

+ 2x

2

− x

2

+ 1) = (x − 1)(x + 1)(x

4

+ 2x

2

+ 1 − x

2

) =

(x − 1)(x + 1)((x

2

)

2

+ 2 · x

2

· 1 − x

2

) = (x − 1)(x + 1)((x

2

+ 1)

2

− x

2

) =

(x − 1)(x + 1)(x

2

+ 1 − x)(x

2

+ 1 + x) = (x − 1)(x + 1)(x

2

− x + 1)(x

2

+ x + 1)

Pytam uczniów, czy nie da się rozłożyć jeszcze tych czynników, które otrzymaliśmy. Do-
chodzimy do wniosku, że nie, bo wyróżnik obydwu jest ujemny:
∆ = 1

2

− 4 · 1 · 1 = 1 − 4 = −3

Zapisujemy pod odpowiednimi nawiasami: ∆ < 0

3

c) W (x) = x

4

− 3x

2

+ 9

Rozwiązanie:
W (x) = x

4

−3x

2

+ 9 = x

4

+ 6x

2

−9x

2

+ 9 = x

4

+ 6x

2

+ 9 − 9x

2

= (x

2

)

2

+ 2 · x

2

·3+3

2

−9x

2

=

(x

2

+ 3)

2

− (3x)

2

= (x

2

+ 3 − 3x)(x

2

+ 3 + 3x) = (x

2

− 3x + 3)(x

2

+ 3x + 3)

Ponownie pytam uczniow, czy można rozłożyć otrzymane czynniki na takie o mniejszym
stopniu. Wspólnie dochodzimy do wniosku, że nie, bo wyróżniki są ujemne:
∆ = 3

2

− 4 · 1 · 3 = 9 − 12 = −3

Zapisujemy pod odpowiednimi nawiasami: ∆ < 0

d) W (x) = x

6

+ 1

Jeśli uczniowie nie mieli żadnych problemów z rozwiązaniem przykładu a) wówczas zadaję
ten przykład do domu. Jeśli jednak były problemy, robimy ten przykład na lekcji. Rozwiązanie:
W (x) = x

6

+ 1 = (x

2

)

3

+ 1

3

= (x

2

+ 1)((x

2

)

2

− x

2

· 1 + 1

2

) = (x

2

+ 1)(x

4

− x

2

+ 1) =

(x

2

+1)(x

4

+2x

2

+1−3x

2

) = (x

2

+1)((x

2

)

2

+2·x

2

·1+1−3x

2

) = (x

2

+1)((x

2

+1)

2

−(

√

3x)

2

) =

(x

2

+ 1)(x

2

+ 1 −

√

3x)(x

2

+ 1 +

√

3x) = (x

2

+ 1)(x

2

−

√

3x + 1)(x

2

+

√

3x + 1)

Tak jak poprzednio pytam uczniów, czy można rozłożyć otrzymane czynniki. Wspólnie
dochodzimy do wniosku, że nie, bo wyróżniki są ujemne:
∆ = (

√

3)

2

− 4 · 1 · 1 = 3 − 4 = −1

Zapisujemy pod odpowiednimi nawiasami: ∆ < 0

e) W (x) = x

8

+ x

4

+ 1

Rozwiązanie:
W (x) = x

8

+ x

4

+ 1 = x

8

+ 2x

4

− x

4

+ 1 = x

8

+ 2x

4

+ 1 − x

4

= (x

4

)

2

+ 2 · x

4

· 1 + 1

2

− x

4

=

(x

4

+ 1)

2

− (x

2

)

2

= (x

4

+ 1 − x

2

)(x

4

+ 1 + x

2

) = (x

4

− x

2

+ 1)(x

4

+ x

2

+ 1)

Mówię uczniom, żeby zauważyli, że takie wielomiany jakie otrzymaliśmy w nawiasach już
wcześniej rozkładaliśmy. Pytam uczniów, czy rozumieli tamte rozkłady. Jeśli nie, to tłu-
maczę ponownie na tym przykładzie. Jeśli natomiast rozumieli, to proszę aby zapisali
końcowy rozkład w domu:
W (x) = (x

2

−

√

3x + 1)(x

2

+

√

3x + 1)(x

2

− x + 1)(x

2

+ x + 1)

f ) W (x) = x

12

− 2x

6

+ 1

Rozwiązanie:
W (x) = x

12

− 2x

6

+ 1 = (x

6

)

2

− 2 · x

6

· 1 + 1

1

= (x

6

− 1)

2

Proszę uczniów, żeby zauważyli, że wielomian x

6

− 1 już rozkładaliśmy. Pytam, czy rozu-

mieli sposób, w jaki to robiliśmy. Jeśli nie, to tłumaczę ponownie. Jeśli tak to zapisujemy
rozwiązanie:
W (x) = [(x − 1)(x + 1)(x

2

− x + 1)(x

2

+ x + 1)]

2

Pytam uczniów, jakie działanie mamy między nawiasami. Jest to iloczyn (mnożenie).
Następnie pytam, co powinniśmy zrobić z tym kwadratem. Dochodzimy do wniosku, że
skoro jest to iloczyn, to każdy czynnik powinien być osobno podniesiony do kwadratu i
zapisujemy:
W (x) = (x − 1)

2

(x + 1)

2

(x

2

− x + 1)

2

(x

2

+ x + 1)

2

4

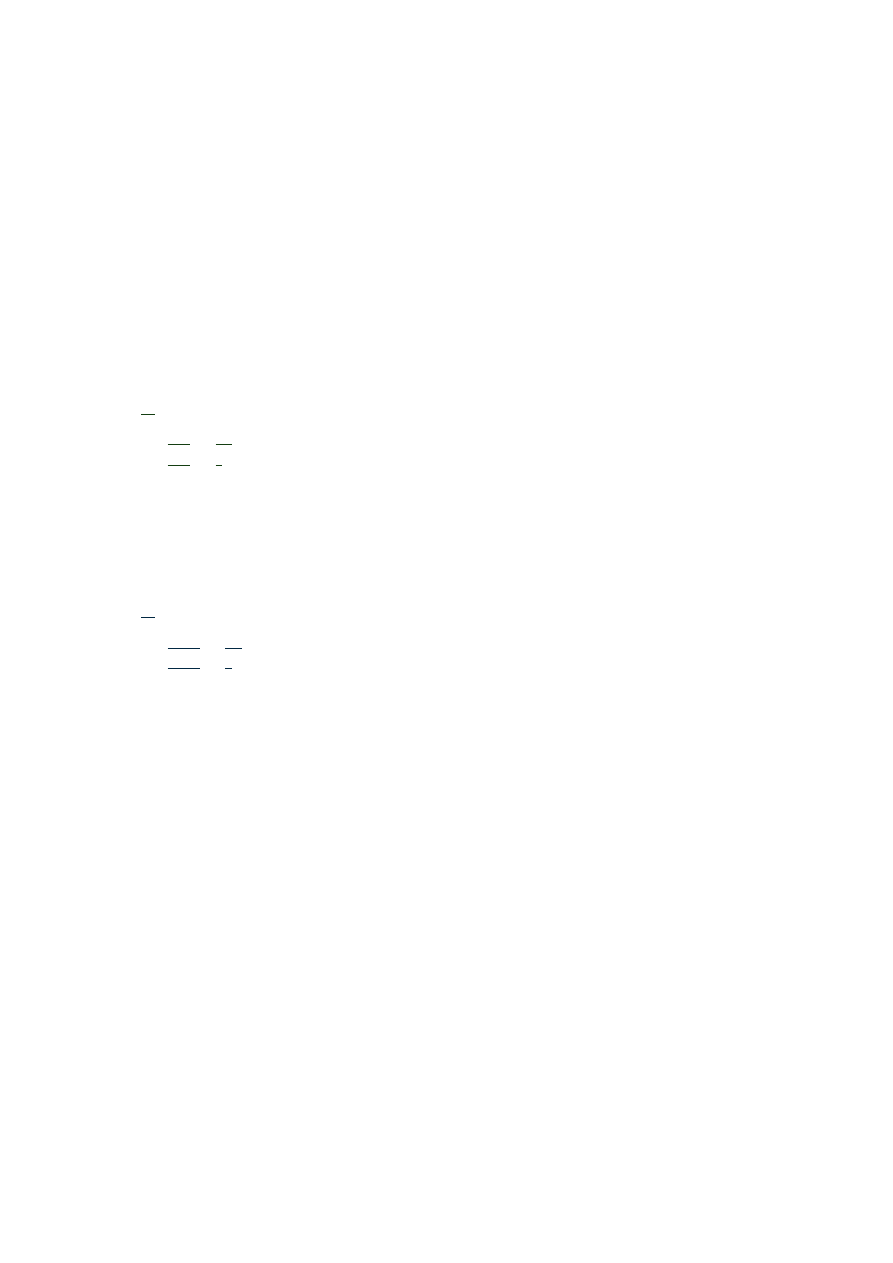
Przechodzimy do kolejnego zadania:
Zad. 3.69
Rozłóż na czynniki wielomiany:
a)W (x) = x

3

(x

2

− 7)

2

− 36x

Jeśli uczeń nie ma pomysłu na rozwiązanie podpowiadam, że można wyłączyć x przed całe
wyrażenie, a następnie skorzystać ze wzoru skróconego mnożenia. Rozwiązanie:
W (x) = x

3

(x

2

− 7)

2

− 36x = x[x

2

(x

2

− 7)

2

− 36] = x[(x(x

2

− 7))

2

− 6

2

] =

x(x(x

2

− 7) − 6)(x(x

2

− 7) + 6) = x(

x

3

− 7x − 6

)(

x

3

− 7x + 6

)

x

3

− 7x − 6 = x

3

− x − 6x − 6 = x(x

2

− 1) − 6(x + 1) = x(x − 1)(x + 1) − 6(x + 1) =

= (x + 1)(x(x − 1) − 6) = (x + 1)(x

2

− x − 6)

∆ = (−1)

2

− 4 · 1 · (−6) = 1 + 24 = 25

√

∆ = 5

x

1

=

1−5

2

=

−4

2

= −2

x

2

=

1+5

2

=

6
2

= 3

(x + 1)(x

2

− x − 6) = (x + 1)(x + 2)(x − 3)

x

3

− 7x + 6 = x

3

− x − 6x + 6 = x(x

2

− 1) − 6(x − 1) = x(x − 1)(x + 1) − 6(x − 1) =

= (x − 1)(x(x + 1) − 6) = (x − 1)(x

2

+ x − 6)

∆ = 1

2

− 4 · 1 · (−6) = 1 + 24 = 25

√

∆ = 5

x

1

=

−1−5

2

=

−6

2

= −3

x

2

=

−1+5

2

=

4
2

= 2

(x − 1)(x

2

+ x − 6) = (x − 1)(x + 3)(x − 2)

Zatem:
W (x) = x(x − 1)(x + 1)(x − 2)(x + 2)(x − 3)(x + 3)

b) W (x) = x

3

(x

2

+ 2)

2

− 9x

Rozwiązanie:
W (x) = x

3

(x

2

+ 2)

2

− 9x = x[x

2

(x

2

+ 2)

2

− 9] = x[(x(x

2

+ 2))

2

− 3

2

] =

x(x(x

2

+ 2) − 3)(x(x

2

+ 2) + 3) = x(

x

3

+ 2x − 3

)(

x

3

+ 2x + 3

)

x

3

+ 2x − 3 = x

3

− x + 3x − 3 = x(x

2

− 1) + 3(x − 1) = x(x − 1)(x + 1) + 3(x − 1) =

= (x − 1)(x(x + 1) + 3) = (x − 1)(x

2

+ x + 3)

∆ = 1

2

− 4 · 1 · 3 = 1 − 12 = −11

x

3

+ 2x + 3 = x

3

− x + 3x + 3 = x(x

2

− 1) + 3(x + 1) = x(x − 1)(x + 1) + 3(x + 1) =

= (x + 1)(x(x − 1) + 3) = (x + 1)(x

2

− x + 3)

∆ = (−1)

2

− 4 · 1 · 3 = 1 − 12 = −11

5

Zatem:
W (x) = x(x − 1)(x + 1)(x

2

+ x + 3)(x

2

− x + 3)

d) W (x) = (x

2

+ 9)

4

− 16x

4

Jeśli uczeń nie wie, podpowiadam, że tutaj należy rozpocząć od zastosowania wzoru skró-
conego mnożenia.
Rozwiązanie:
W (x) = (x

2

+ 9)

4

− 16x

4

= [(x

2

+ 9)

2

]

2

− (4x

2

)

2

= [(x

2

+ 9)

2

− 4x

2

][(x

2

+ 9)

2

+ 4x

2

] =

[(x

2

+ 9)

2

− (2x)

2

][x

4

+ 18x

2

+ 81 + 4x

2

] = [(x

2

+ 9 − 2x)(x

2

+ 9 + 2x)][x

4

+ 22x

2

+ 81] =

[(x

2

− 2x + 9)(x

2

+ 2x + 9)][x

4

+ 22x

2

+ 81]

W tym miejscu pytam, czy otrzymane czynniki stopnia 2 da się jeszcze rozłożyć. Licząc
wyróżniki dochodzimy do wniosku, że nie:
∆ = 2

2

− 4 · 1 · 9 = 4 − 36 = −32 < 0

Rozkładamy dalej trzeci otrzymany czynnik. Jeśli uczeń nie wie, jak to policzyć pod-
powiadam, że lepiej rozbić sobie tutaj to 81 niż 22x

2

.

x

4

+ 22x

2

+ 81 = x

4

+ 22x

2

+ 121 − 40 = (x

2

)

2

+ 2 · x

2

· 11 + 11

2

− 40 = (x

2

+ 11)

2

− (

√

40)

2

=

(x

2

+ 11 −

√

40)(x

2

+ 11 +

√

40) = (x

2

− 2

√

10 + 11)(x

2

+ 2

√

10 + 11)

Pytam uczniów, czy otrzymane czynniki da się jeszcze rozłożyć. Wspólnie dochodzimy do
wniosku, że nie, ponieważ są to wyrażenia postaci x

2

+ a, gdzie a w obu przypadkach jest

liczbą dodatnią.

Następnie przechodzimy do kolejnego zadania:
Zad. 3.70
Rozłóż na czynniki wielomiany:
a) W (x) = 2x

3

− x

2

+ 3

Mówię uczniom, że w tym zadaniu najłatwiej będzie znaleźć jeden z pierwiastków i zas-
tosować twierdzenie B ´

ezout. Wtedy dostaniemy rozkład na dwa czynniki, z których jeden

będzie liniowy, a drugi kwadratowy. A z kwadratowym umiemy sobie poradzić.

Rozwiązanie:
Szukamy pierwiastków całkowitych. Przypominam, że jeśli one istnieją, to muszą być dziel-
nikami wyrazu wolnego. Wypisujemy zatem dzielniki wyrazu wolnego:
{−3, −1, 1, 3}

Uczniowie mogą sprawdzać, czy dana liczba jest pierwiastkiem podstawiając ją do wzoru
lub dzieląc schematem Hornera i sprawdzając, czy reszta wynosi 0. Poniżej pokażę pier-
wszy z wymienionych sposobów (zamieszczam tylko obliczenia dla liczb, które okazały się
pierwiastakmi):
W (−1) = 2 · (−1)

3

− (−1)

2

+ 3 = −2 − 1 + 3 = 0

Schemat Hornera:

2

-1

0

3

-1

2

-3

3

0

Zatem: W (x) = (x + 1)(2x

2

− 3x + 3)

6

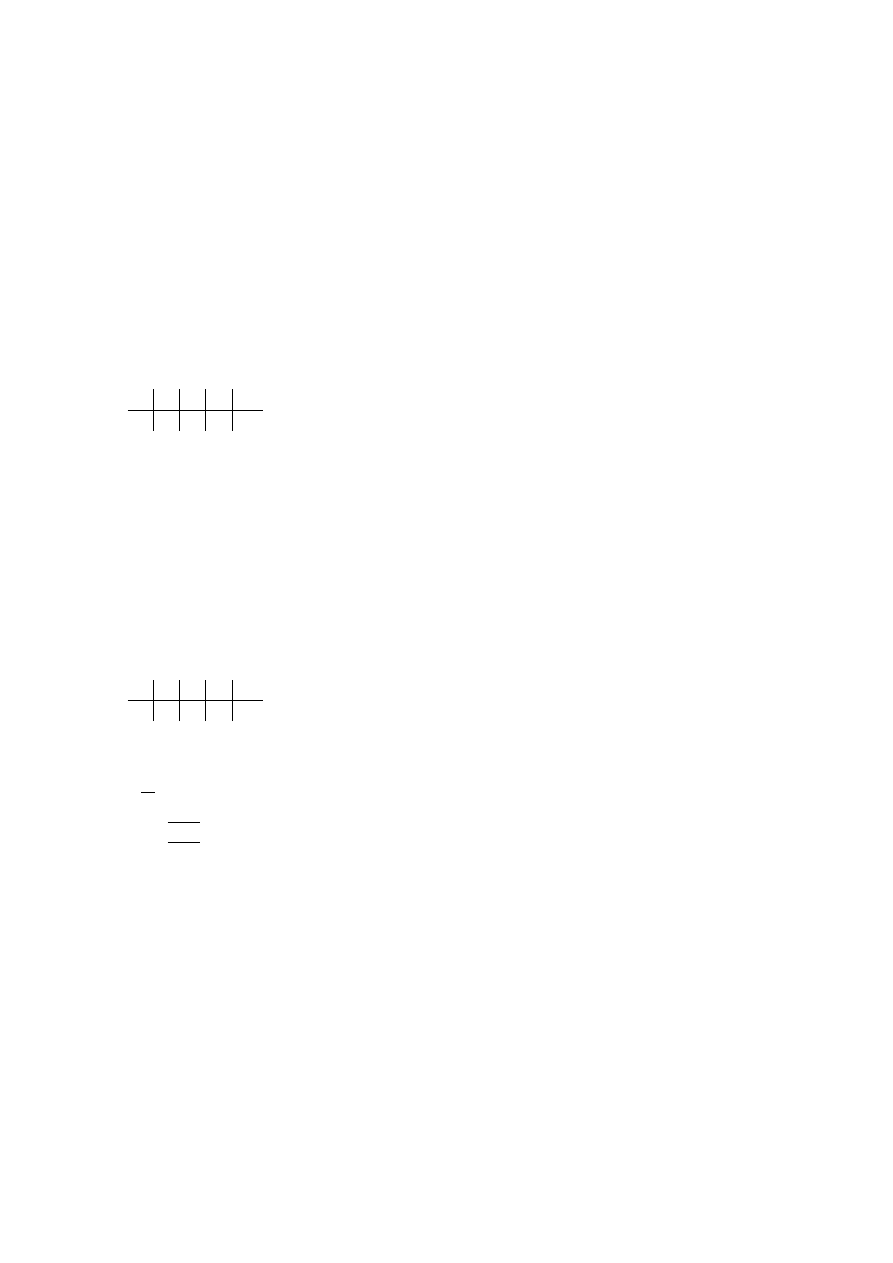
Dochodzimy do wniosku, że czynnika kwadratowego nie da się już rozłożyć ponieważ jego
wyróżnik jest ujemny:
∆ = (−3)

2

− 4 · 2 · 3 = 9 − 24 = −15 < 0

b) W (x) = x

3

+ 5x

2

+ 3x − 9

Rozwiązanie:
Liczby, które mogą być pierwiastkami całkowitymi:
{−9, −3, −1, 1, 3, 9}
W (−3) = (−3)

3

+ 5 · (−3)

2

+ 3 · (−3) − 9 = −27 + 45 − 9 − 9 = 0

W (1) = 1

3

+ 5 · 1

2

+ 3 · 1 − 9 = 1 + 5 + 3 − 9 = 0

Schemat Hornera:

1

5

3

-9

1

1

6

9

0

Zatem: W (x) = (x − 1)(x

2

+ 6x + 9) = (x − 1)(x + 3)

2

c) W (x) = x

3

+ 4x

2

+ x − 6

Rozwiązanie:
Liczby, które mogą być pierwiastkami całkowitymi:
{−6, −3, −2, −1, 1, 2, 3, 6}
W (−3) = (−3)

3

+ 4 · (−3)

2

− 3 − 6 = −27 + 36 − 3 − 6 = 0

W (−2) = (−2)

3

+ 4 · (−2)

2

− 2 − 6 = −8 + 16 − 2 − 6 = 0

W (1) = 1

3

+ 4 · 1

2

+ 1 − 6 = 1 + 4 + 1 − 6 = 0

Schemat Hornera:

1

4

1

-6

1

1

5

6

0

Zatem: W (x) = (x − 1)(x

2

+ 5x + 6)

Rozkładamy czynnik kwadratowy:
∆ = 5

2

− 4 · 1 · 6 = 25 − 24 = 1

√

∆ = 1

x

1

=

−5−1

2

= −3

x

2

=

−5+1

2

= −2

Zatem: W (x) = (x − 1)(x + 2)(x + 3)

d) W (x) = 2x

3

− 5x

2

− x + 6

Rozwiązanie:
Liczby, które mogą być pierwiastkami całkowitymi:
{−6, −3, −2, −1, 1, 2, 3, 6}
W (−1) = 2 · (−1)

3

− 5 · (−1)

2

− (−1) + 6 = −2 − 5 + 1 + 6 = 0

W (2) = 2 · 2

3

− 5 · 2

2

− 2 + 6 = 16 − 20 − 2 + 6 = 0

7

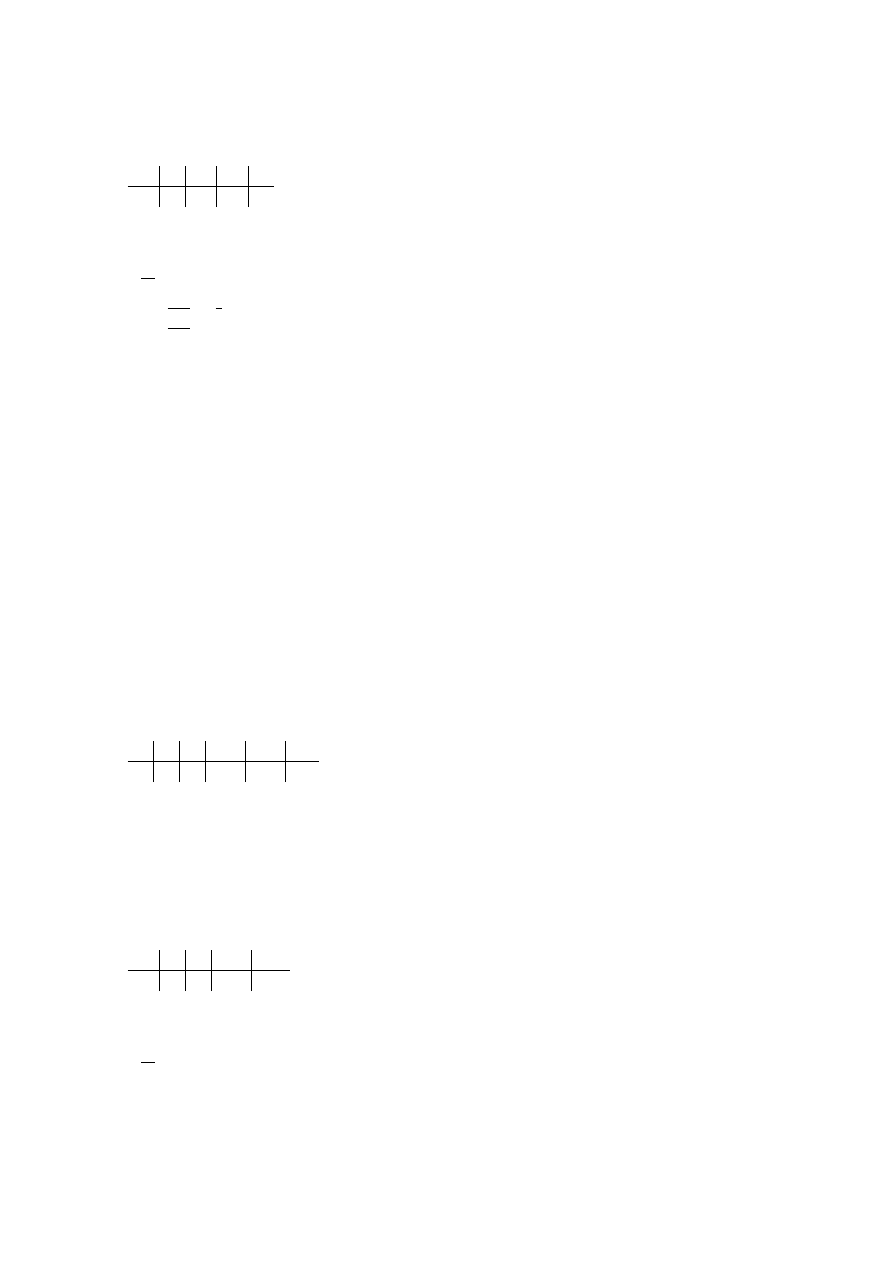
Schemat Hornera:

2

-5

-1

6

-1

2

-7

6

0

Zatem: W (x) = (x + 1)(2x

2

− 7x + 6)

Rozkładamy czynnik kwadratowy:
∆ = (−7)

2

− 4 · 2 · 6 = 49 − 48 = 1

√

∆ = 1

x

1

=

7−1

4

=

3
2

x

2

=

7+1

4

= 2

Zatem: W (x) = (x + 1)(x − 2)(2x − 3)

Przechodzimy do kolejnego zadania:
Zad. 3.71
Rozłóż na czynniki wielomany:
a) W (x) = x

4

+ 3x

3

− 15x

2

− 19x + 30

Podpowiadam uczniom, że to zadanie jest bardzo podobne do poprzedniego z tym, że tutaj
czasami trzeba będzie 2 razy zastosować schemat Hornera.

Rozwiązanie:
Liczby, które mogą być pierwiastkami całkowitymi:
{−30, −15, −10, −6, −5, −3, −2, −1, 1, 2, 3, 5, 6, 10, 15}
W (1) = 1

4

+ 3 · 1

3

− 15 · 1

2

− 19 · 1 + 30 = 1 + 3 − 15 − 19 + 30 = 0

W (−2) = (−2)

4

+ 3 · (−2)

3

− 15 · (−2)

2

− 19 · (−2) + 30 = 16 − 24 − 60 + 38 + 30 = 0

W (3) = 3

4

+ 3 · 3

3

− 15 · 3

2

− 19 · 3 + 30 = 81 + 81 − 135 − 57 + 30 = 0

W (−5) = (−5)

4

+ 3 · (−5)

3

− 15 · (−5)

2

− 19 · (−5) + 30 = 625 − 375 − 375 + 95 + 30 = 0

Schemat Hornera:

1

3

-15

-19

30

1

1

4

-11

-30

0

Zatem: W (x) = (x − 1)(x

3

+ 4x

2

− 11x − 30)

Oznaczamy sobie wielomian trzeciego stopnia przez F (x) i szukamy jego pierwiastka całkowitego.
Zbiór liczb, które mogą być takim pierwiastkiem jest taki sam jak dla wielomianu W (x).
F (−2) = (−2)

3

+ 4 · (−2)

2

− 11 · (−2) − 30 = −8 + 16 + 22 − 30 = 0

F (−5) = (−5)

3

+ 4 · (−5)

2

− 11 · (−5) − 30 = −125 + 100 + 55 − 30 = 0

F (3) = 3

3

+ 4 · 3

2

− 11 · 3 − 30 = 27 + 36 − 33 − 30 = 0

Schemat Hornera:

1

4

-11

-30

-2

1

2

-15

0

Zatem: W (x) = (x − 1)(x + 2)(x

2

+ 2x − 15)

Czynnik kwadratowy rozkładamy licząc wyróżnik:
∆ = 2

2

− 4 · 1 · (−15) = 4 + 60 = 64

√

∆ = 8

8

x

1

=

−2−8

2

= −5

x

2

=

−2+8

2

= 3

Zatem: W (x) = (x − 1)(x + 2)(x + 5)(x − 3)

b) W (x) = x

4

− x

3

− x

2

− x − 2

Rozwiązanie:
Liczby, które mogą być pierwiastkami całkowitymi:
{−2, −1, 1, 2}
W (2) = 2

4

− 2

3

− 2

2

− 2 − 2 = 16 − 8 − 4 − 2 − 2 = 0

W (−1) = (−1)

4

− (−1)

3

− (−1)

2

− (−1) − 2 = 1 + 1 − 1 + 1 − 2 = 0

Schemat Hornera:

1

-1

-1

-1

-2

-1

1

-2

1

-2

0

Zatem: W (x) = (x + 1)(x

3

− 2x

2

+ x − 2)

Zwracam uwagę uczniów, że wielomian trzeciego stopnia, który otrzymaliśmy bardzo łatwo
rozłożyć metodą grupowania wyrazów:
x

3

−2x

2

+x−2 = x

2

(x−2)+(x−2) = (x−2)(x

2

+1) Zatem: W (x) = (x+1)(x−2)(x

2

+1)

d) W (x) = 4x

4

− 12x

3

+ 25x

2

− 48x + 36

W tym przykładzie nie ma pierwiastków całkowitych. Mówię o tym uczniom i pytam, co
można w takim wypadku zrobić. Dochodzimy do wniosku, że można znaleźć pierwiastki
wymierne. Przypominamy, że są to liczby postaci

p
q

, gdzie p są dzielnikami wyrazu wolnego,

a q są dzielnikami współczynnika przy najwyższej potędze. Wypisujemy:

• dzielniki wyrazu wolnego: {−18, −12, −9, −6, −4, −3, −2, −1, 1, 2, 3, 4, 6, 9, 12, 18}

• dzielniki współ. przy najwyższej potędze: {−4, −2, −1, 1, 2, 4}

•

p
q

∈ {−18, −12, −9, −6, −

9
2

, −4, −3, −

9
4

, −2, −

3
2

, −1, −

3
4

, −

1
2

, −

1
4

,

1
4

,

1
2

,

3
4

, 1,

3
2

, 2,

9
4

, 3, 4,

9
2

, 6, 9, 12, 18}

Tutaj proponuję sprawdzać, czy liczba jest pierwiastkiem dzieląc za pomocą schhematu
Hornera i sprawdzając resztę:
Schemat Hornera:

4

-12

25

-48

36

3
2

4

-6

16

-24

0

Zatema: W (x) = (x −

3
2

)(4x

3

− 6x

2

+ 16x − 24)

Ponownie proponuję schemat Hornera:

4

-6

16

-24

3
2

4

0

16

0

Zatem: W (x) = (x −

3
2

)

2

(4x

2

+ 16)

9

Następnie przechodzimy do najmniejszej wspólnej wielokrotności i największego wspól-
nego dzielnika dwóch wielomianów. Zapisuję na tablicy:

N W D(44, 72) =

N W W (44, 72) =

i proszę uczniów, żeby policzyli największy wspólny dzielnik i najmniejszą wspólną wielokrot-
ność podanych liczb. Po chwili pytam o wynik największego wspólnego dzielnika. Osobę,
która poda prawidłowy wynik proszę, żeby pokazała sposób liczenia na tablicy.
(Jeśli uczeń przy tablicy poda rozwiązanie za pomocą algorytmu Euklidesa, zapytam kto
zrobił to innym sposobem i również poproszę go do tablicy.)

Prawidłowe rozwiązanie:

72

2

44

2

36

2

22

2

18

2

11

11

9

3

1

3

3

1

N W D(44, 72) =

2 · 2

= 4

Pytam ucznia, dlaczego wybrał akurat te liczby. Prawidłowa odpowiedź: bo te liczby
pojawiły się w rozkładach zarówno pierwszej jak i drugiej liczby.

Pytam uczniów, jak wyznacza się NWD więcej niż dwóch liczb. Oczekuję odpowiedzi,
że wówczas postępujemy analogicznie, ale bierzemy pod uwagę większą liczbę rozkładów.
Następnie proszę uczniów, aby przypomnieli definicję największego wspólnego dzielnika
liczb. Wspólnie ustnie formułujemy tę definicję:
Największym wspólnym dzielnikiem danych liczb jest największa liczba dzieląca każdą z
nich.

Później przechodzimy dalej do najmniejszej wspólnej wielokrotności:
Pytam uczniów o wynik i również proszę do tablicy ucznia, który poda prawidłowy wynik.

Poprawne rozwiązanie:

72

2

44

2

36

2

22

2

18

2

11

11

9

3

1

3

3

1

N W W (44, 72) = 2

3

· 3

2

· 11 = 792

Pytam ucznia, dlaczego wybrał te liczby i zapisał je tyle razy.

Oczękuję odpowiedzi,

że muszą tu występować wszystkie liczby, które pojawiły się w rozkłach, a liczba ich wys-
tąpień bierze się z rozkładu, w którym występowały największą liczbę razy.

10

Pytam jeszcze jak wyznacza się NWW więcej niż dwóch liczb. Wspólnie dochodzimy do
wniosku, że należy wówczas postępować analogicznie z tą różnicą, że należy brać pod uwagę
większą liczbę rozkładów.
Następnie proszę uczniów, aby przypomnieli definicję najmniejszej wspólnej wielokrotności
liczb. Wspólnie ustnie formułujemy tę definicję:
Najmniejszą wspólną wielokrotnością danych liczb jest najmniejsza liczba dzieląca się przez
każdą z nich.

Mówię uczniom, że bardzo podobnie definiujemy i wyznaczamy największy wspólny dziel-
nik i najmniejszą wspólną wielokrotność wielomianów. Umiemy rozkładać wielomiany na
czynniki, więc do wyznaczenia NWD dwóch wielomianów wystarczy wziąć wszystkie czyn-
niki, które powtarzają się w rozkładach, a do wyznaczenia NWW należy wziąć wszystkie
czynniki, które pojawiły się w rozkładach z najwyższymi z występujących potęg.
Dyktuję do zeszytów definicje:
Najmniejszą wspólną wielokrotnością danych wielomianów nazywami taki wielomian stop-
nia możliwie najniższego, dla którego dane wielomiany są jego dzielnikami.
Największym wspólnym dzielnikiem danych wielomianów nazywamy wielomian stopnia
możliwie najwyższego, który jest dzielnikiem każdego z danych wielomianów.

Przechodzimy do zadań:
Zad 3.72
Znajdź najmniejszą wspólną wielokrotność wielomianów:
a) x

2

− 1; x

3

− x

2

+ x − 1; x

3

+ x

2

+ x + 1; x

4

− 1;

Rozkładamy na czynniki każdy wielomian osobno metodami poznanymi wcześniej:
x

2

− 1 = (x − 1)(x + 1)

x

3

− x

2

+ x − 1 = x

2

(x − 1) + (x − 1) = (x − 1)(x

2

+ 1)

x

3

+ x

2

+ x + 1 = x

2

(x + 1) + (x + 1) = (x + 1)(x

2

+ 1)

x

4

− 1 = (x

2

− 1)(x

2

+ 1) = (x − 1)(x + 1)(x

2

+ 1)

i wypisujemy wielomian, który jest najmiejszą wspólną wielokrotnością:
N W W (x

2

− 1, x

3

− x

2

+ x − 1, x

3

+ x

2

+ x + 1, x

4

− 1) = (x − 1)(x + 1)(x

2

+ 1) = x

4

− 1

c) x

3

+ 1; x

3

− 1; x

4

+ x

2

+ 1;

Rozwiązanie:
x

3

+ 1 = (x + 1)(x

2

− x + 1)

x

3

− 1 = (x − 1)(x

2

+ x + 1)

x

4

+x

2

+1 = x

4

+2x

2

−x

2

+1 = x

4

+2x

2

+1−x

2

= (x

2

+1)

2

−x

2

= (x

2

+1−x)(x

2

+1+x) =

(x

2

− x + 1)(x

2

+ x + 1)

N W W (x

3

+ 1, x

3

− 1, x

4

+ x

2

+ 1) = (x + 1)(x − 1)(x

2

− x + 1)(x

2

+ x + 1) = (x

2

−

1)(x

4

+ x

2

+ 1) = x

6

− 1

11

d) x

3

+ 9x

2

+ 27x + 27; x

2

+ 6x + 9; x

2

− 9; x

4

− 81;

Rozwiązanie:
x

3

+ 9x

2

+ 27x + 27 = (x + 3)

3

x

2

+ 6x + 9 = (x + 3)

2

x

2

− 9 = (x − 3)(x + 3)

x

4

− 81 = (x

2

− 9)(x

2

+ 9) = (x − 3)(x + 3)(x

2

+ 9)

N W W (x

3

+ 9x

2

+ 27x + 27, x

2

+ 6x + 9, x

2

− 9, x

4

− 81) = (x − 3)(x + 3)

3

(x

2

+ 9)

Zad. 3.73
Znajdź największy wspólny dzielnik wielomianów:
a) x

3

+ 3x

2

+ 4x + 12; x

3

+ 4x

2

+ 4x + 3;

Rozwiązanie:
x

3

+ 3x

2

+ 4x + 12 = x

2

(x + 3) + 4(x + 3) = (x + 3)(x

2

+ 4)

x

3

+4x

2

+4x+3 = x

3

+3x

2

+x

2

+3x+x+3 = x

2

(x+3)+x(x+3)+(x+3) = (x+3)(x

2

+x+1)

N W D(x

3

+ 3x

2

+ 4x + 12, x

3

+ 4x

2

+ 4x + 3) = x + 3

b) x

4

− 7x

3

+ 8x

2

+ 28x − 48; x

3

+ 2x

2

− 29x + 42;

Rozwiązanie:
x

4

− 7x

3

+ 8x

2

+ 28x − 48 Schemat Hornera:

1

-7

8

28

-48

2

1

-5

-2

24

0

Zatem: x

4

− 7x

3

+ 8x

2

+ 28x − 48 = (x − 2)(x

3

− 5x

2

− 2x + 24)

Schemat Hornera:

1

-5

-2

24

3

1

-2

-8

0

Zatem: (x − 2)(x

3

− 5x

2

− 2x + 24) = (x − 2)(x − 3)(x

2

− 2x − 8)

∆ = (−2)

2

− 4 · 1 · (−8) = 4 + 32 = 36

√

∆ = 6

x

1

=

2−6

2

= −2

x

2

=

2+6

2

= 4

Zatem: x

4

− 7x

3

+ 8x

2

+ 28x − 48 = (x − 2)(x − 3)(x + 2)(x − 4)

x

3

+ 4x

2

+ 4x + 3

Schemat Hornera:

1

2

-29

42

2

1

4

-21

24

12

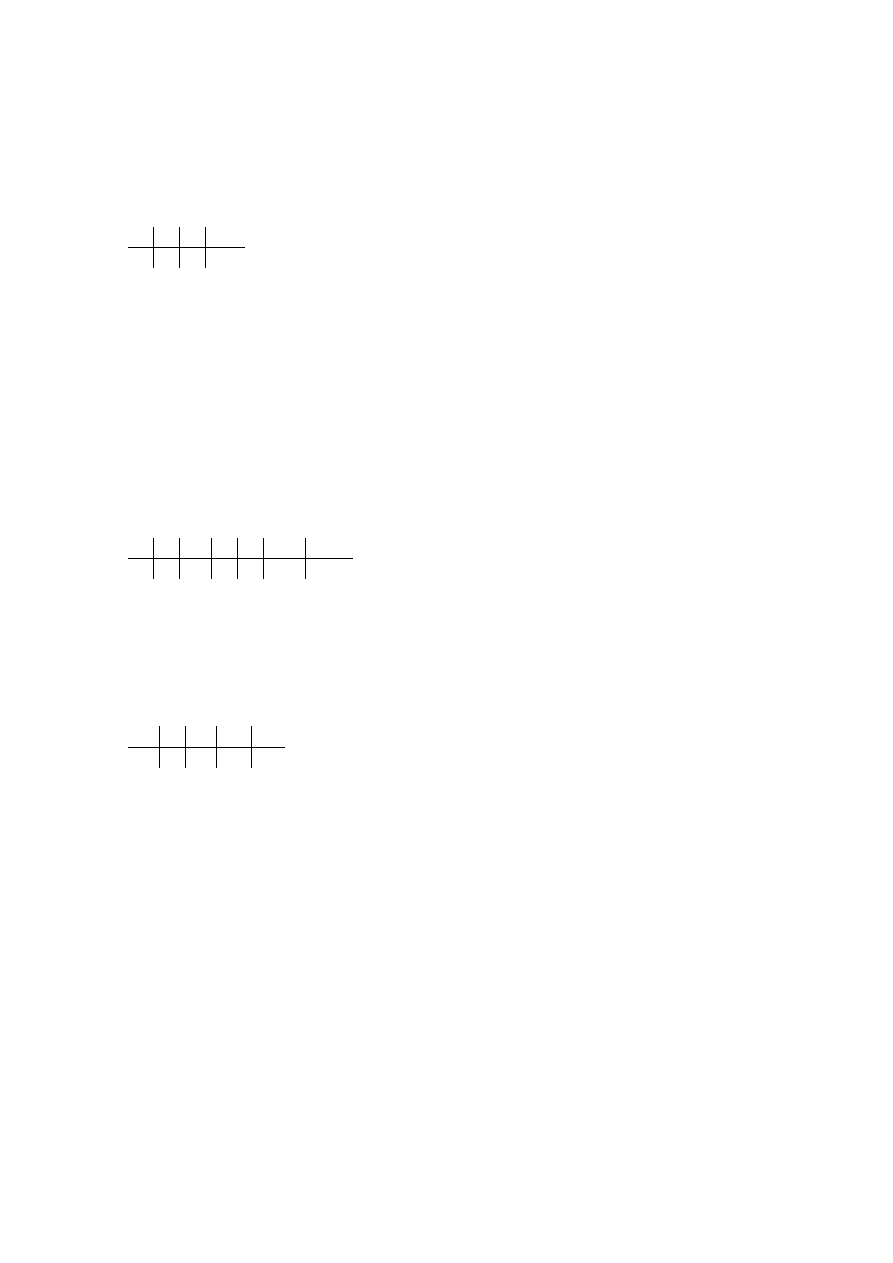
Zatem: x

3

+ 4x

2

+ 4x + 3 = (x − 2)(x

2

+ 4x − 21)

Schemat Hornera:

1

4

-21

3

1

7

0

Zatem: (x − 2)(x

2

+ 4x − 21) = (x − 2)(x − 3)(x + 7)

Zatem: x

3

+ 4x

2

+ 4x + 3 = (x − 2)(x − 3)(x + 7)

N W D(x

4

− 7x

3

+ 8x

2

+ 28x − 48, x

3

+ 2x

2

− 29x + 42) = (x − 2)(x − 3) = x

2

− 5x + 6

d) x

5

− x

4

+ 324x − 324; x

3

− 5x

2

+ 12x + 18

Rozwiązanie:
x

5

− x

4

+ 324x − 324

Schemat Hornera:

1

-1

0

0

324

-324

1

1

0

0

0

324

0

Zatem: x

5

− x

4

+ 324x − 324 = (x − 1)(x

4

+ 324) = (x − 1)(x

4

+ 36x

2

+ 324 − 36x

2

) =

(x − 1)((x

2

+ 18)

2

− 36x

2

) = (x − 1)(x

2

− 6x + 18)(x

2

+ 6x + 18)

∆ = 36 − 4 · 18 = 36 − 72 = −36 < 0

x

3

− 5x

2

+ 12x + 18

Schemat Hornera:

1

-5

12

18

-1

1

-6

18

0

Zatem: x

3

− 5x

2

+ 12x + 18 = (x + 1)(x

2

− 6x + 18)

N W D(x

5

− x

4

+ 324x − 324, x

3

− 5x

2

+ 12x + 18) = x

2

− 6x + 18

Zadanie domowe:

Jako pracę domową zadam uczniom przykłady z zadania, na którym skończymy lekcję.
Być może uczniowie będą mieli zadane przykłady z podręcznika dotyczące pierwszej lekcji
z tego dnia.

13