
Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
Schody
Dane:
Schody płytowe monolityczne z belkami spocznikowymi.
Szerokość biegu,
szer
150 cm
⋅
=
Obciążenie zmienne,
qz
3.00
kN
m
2
⋅
=
Beton klasy B15,
fcd
8.0 MPa
⋅
=
fctd
0.73 MPa
⋅
=
fctm
1.6 MPa
⋅
=
fck
12 MPa
⋅
=
Ecm
27 GPa
⋅
=
α
1.00
=
Stal klasy A-II,
fyd
310 MPa
⋅
=
fyk
355 MPa
⋅
=
ξeff.lim
0.55
=
Na schodach przewiduje się ułożenie warswty lastryka o gr. 3cm.
Wymiary schodka:
hschod
20 cm
⋅
=
sschod
25 cm
⋅
=
Ciężar objętościowy materiałów i współczynniki obciążenia przyjęto wg PN-82/B-02001.
Obliczenia:
Zebranie obciążeń:
Wartości charakterystyczne ciężaru objętościowego potrzebynych materiałów:
Beton zbrojony niezagęszczony,
qbznzg
24
kN
m
3
⋅
=
Beton niezagęszczony,
qbnzg
23
kN
m
3
⋅
=
Lastryko,
qlast
22
kN
m
3
⋅
=

Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
1. Płyta biegowa
Przyjęto płytę grubości,
grpł.b
12 cm
⋅
=
obciążenie stałe
•
płyta,
qpłyta.b
grpł.b qbznzg
⋅
1.1
⋅
=
qpłyta.b 3.168 10
3
×
Pa
=
stopnie,
qstopnie
0.5 hschod
⋅
qbnzg
⋅
1.1
⋅
=
qstopnie 2.53 10
3
×
Pa
=
lastryko,
qlastryko
0.03 cm
⋅
qlast
⋅
1.2
⋅
=
qlastryko 7.92 Pa
=
Suma obciążeń stałych,
qstałe.b
qpłyta.b qstopnie
+
qlastryko
+
=
qstałe.b 5.706 kPa
⋅
=
obciążenie zmienne
•
qzmienne
qz 1.3
⋅
=
qzmienne 3.9 10
3
×
Pa
=
2. Płyta spocznikowa
Przyjęto płytę grubości,
grpł.s
8 cm
⋅
=
obciążenie stałe
•
plyta,
qpłyta.s
grpł.s qbznzg
⋅
1.1
⋅
=
qpłyta.s 2.112 10
3
×
Pa
=
lastryko j.w.,
qlastryko 7.92 Pa
=
Suma obciążeń stałych,
qstałe.s
qpłyta.s
qlastryko
+
=
qstałe.s 2.12 10
3
×
Pa
=
obciążenie zmienne j.w.
•
qzmienne 3.9 10
3
×
Pa
=
3. Belka spocznikowa
Przyjęto belkę o wymiarach,
hbelki
40cm
=
bbelki
20cm
=
obciążenie stałe
•
belka,
qbelka
bbelki hbelki grpł.s
−
(
)
⋅
qbznzg
⋅
1.1
⋅
=
qbelka 1.69 10
3
×
kg
s
2
=
płyta biegowa,
qpb
qpłyta.b qstopnie
+
(
)
210
⋅
cm
⋅
0.5
⋅
=
qpb 5.983 10
3
×
kg
s
2
=

Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
lastryko,
ql
2 qlastryko
⋅
210
⋅
cm
⋅
0.5
⋅
=
ql 16.632
kg
s
2
=
płyta spocznikowa,
qs
qpłyta.s 150
⋅
cm
⋅
0.5
⋅
=
qs 1.584 10
3
×
kg
s
2
=
Suma obciążeń stałych,
qstałe.bs
qbelka qpb
+
ql
+
qs
+
=
qstałe.bs 9.273 10
3
×
kg
s
2
=
obciążenie zmmienne
•
qzmienne.bs
qz 210cm 150cm
+
(
)
⋅
0.5
⋅
1.3
⋅
=
qzmienne.bs 7.02 10
3
×
kg
s
2
=
Schemat statyczny:
nr 1
•

Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
nr 2
•
Obliczenie zbrojenia:
1. Płyta biegowa
Wybrano płyte biegową, w której występuje największy moment zginający. Dla reszty
płyt przyjęto zbrojenie spęłniajace wymagania występujące w najbardziej "zginanej"
płycie biegowej.
Płytę biegową projketuję, jako płytę jednokierunkowo zginaną.
Dane:
dane betonu i stali podane na początku
•
wymiary przekroju:
•
h
12cm
=
b
100cm
=
ś
rednica zbrojenia:
•
ϕ
6mm
=
klasa ekspozycji
•
X0 - brakryzyka korozji lub agresji środowiska
otulina
•
cmin
10mm
=
∆c
5mm
=
Stan graniczny nośności:
a) zbrojenie główne
Msd
4.989 kN
⋅
m
⋅
=
a1
cmin ∆c
+
ϕ
2
+
=
a1 0.018m
=
d
h
a1
−
=
d
0.102 m
=
sb
Msd
α fcd
⋅
b
⋅
d
2
⋅
=
sb 0.06
=
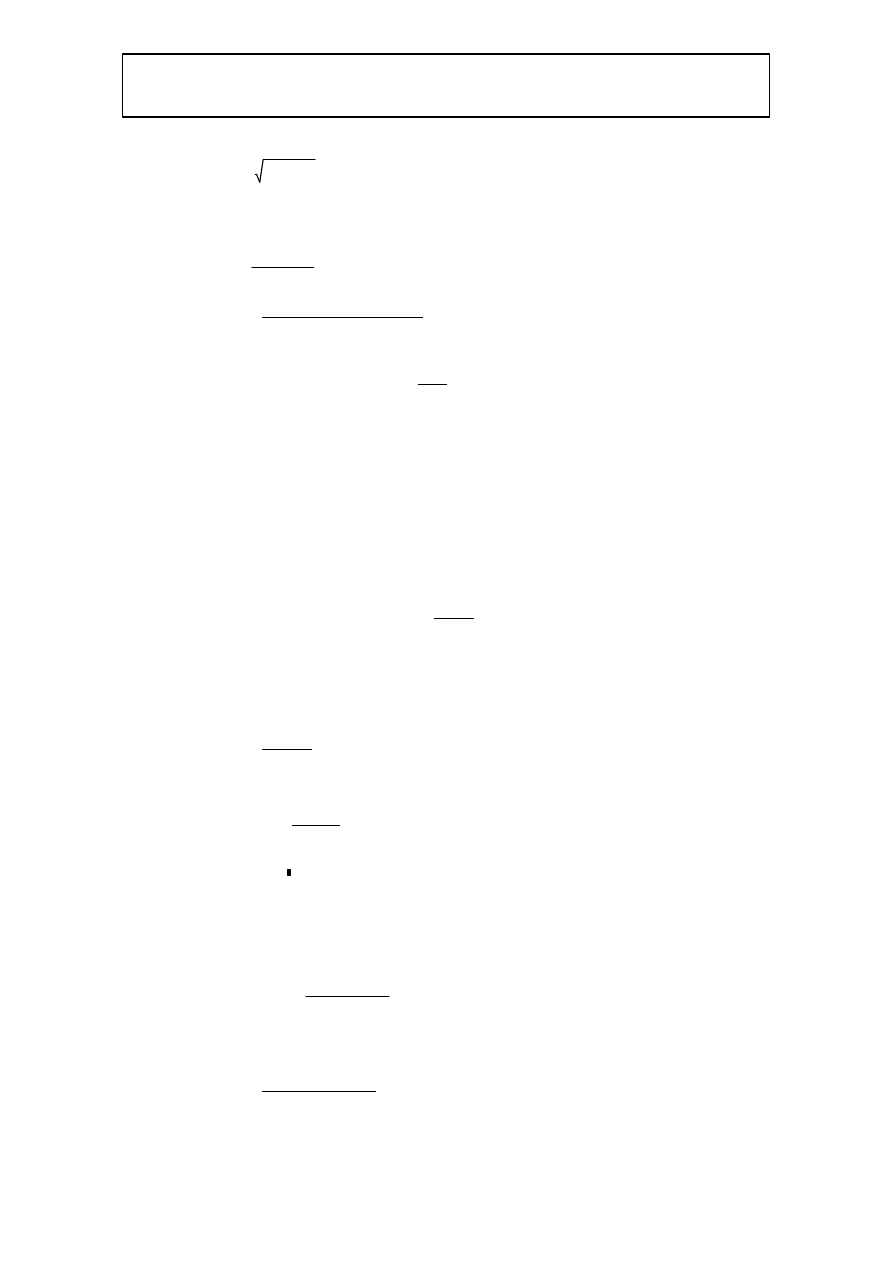
Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
ξeff
1
1
2 sb
⋅
−
−
=
ξeff 0.062
=
< ξ
eff.lim
0.55
=
ζeff
1
0.5
ξeff
⋅
−
=
ζeff 0.969
=
As1.req
Msd
ζeff d
⋅
fyd
⋅
=
As1.req 1.628 cm
2
⋅
=
minimalne pole zbrojenia
•
1.
As.min1
0.0013 b
⋅
d
⋅
=
As.min1 1.326 cm
2
⋅
=
2.
As.min2
0.26 b
⋅
d
⋅
fctm
fyk
⋅
=
As.min2 1.195 cm
2
⋅
=
3.
kc
0.4
=
k
0.8
=
fct.eff
fctm
=
σs.lim
400 MPa
⋅
=
Pole A
ct
rozciąganej strefy prostokątnego przekroju elementu
ż
elbetowego przy zginaniu oblicza się ze wzoru:
Act
0.5 b
⋅
h
⋅
=
Act 0.06 m
2
=
As.min3
kc k
⋅
fct.eff
⋅
Act
σs.lim
⋅
=
As.min3 0.768 cm
2
⋅
=
Minimalne pole zbrojenia wynosi:
max As.min1 As.min2
,
As.min3
,
(
)
1.326 cm
2
⋅
=
rozstaw
•
As.ϕ6
0.28cm
2
=
sreq
As.ϕ6
As1.req
100
⋅
cm
=
sreq 17.197 cm
⋅
=
s
ϕ
≥
0.6cm
⋅
=
ϕ
s
2.0cm
≥
s
25.0cm
≤
s
1.2 h
⋅
≤
1.2 h
⋅
14.4 cm
⋅
=
sprov
14.0cm
=
As.prov
As.ϕ6 100
⋅
cm
sprov
=
As.prov 2.00 cm
2
⋅
=
przyjęto zbrojenie
•
ϕ
6 mm
⋅
=
A-II co 14cm
As1
As.prov 2.00 cm
2
⋅
=
=
Z uwagi możliwości wystapienia momentu częściowego utwierdzenia, co drugi
pręt należy odgiąc do góry.

Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
b) zbrojenie rozdzielcze
As.rozdz 0.15 As.prov
⋅
≥
0.15 As.prov
⋅
0.30 cm
2
⋅
=
srozdz 30.0cm
≤
srozdz.prov
25.0cm
=
As.rozdz.prov
As.ϕ6
srozdz.prov
100
⋅
cm
=
As.rozdz.prov 1.12 cm
2
⋅
=
Przyjęto zbrojenie rozdzielcze:
ϕ
6 mm
⋅
=
co 25cm
As.rozdz.prov 1.12 cm
2
⋅
=
c) zbrojenie na ścinanie
Vsd
11.843kN
=
przyjęto:
ϕl
0
=
k
1
=
VRd1
0.35 fctd
⋅
k
⋅
1.2
40
ϕl
⋅
+
(
)
⋅
b
⋅
d
⋅
=
VRd1 31.273 kN
⋅
=
Vsd VRd1
≤
υ
0.6 1
fck
250 MPa
⋅
−
=
υ
0.571
=
VRd2
0.5
υ
⋅
fcd
⋅
b
⋅
d
⋅
=
VRd2 233.05 kN
⋅
=
Vsd VRd2
≤
Jest to odcinek I rodzaju - zbrojenie na ścinanie nie jest potrzebne.
Stan graniczny użytkowania:
a) szerokość rozwarcia rys:
ukośne
•
Nie trzeba sprawdzać, bo jest to odcinek I rodzaju
prostopadłe
•
d
h
0.85
=
Zatem można skorzystać z metody uproszczonej (zał. D PN).
Stopień zbrojenia:
ρ1
As1
b d
⋅
100
⋅
=
ρ1 0.2
=
zatem
ζ
0.90
=
σs
Msd
ζ d
⋅
As1
⋅
=
σs 271.7 MPa
⋅
=
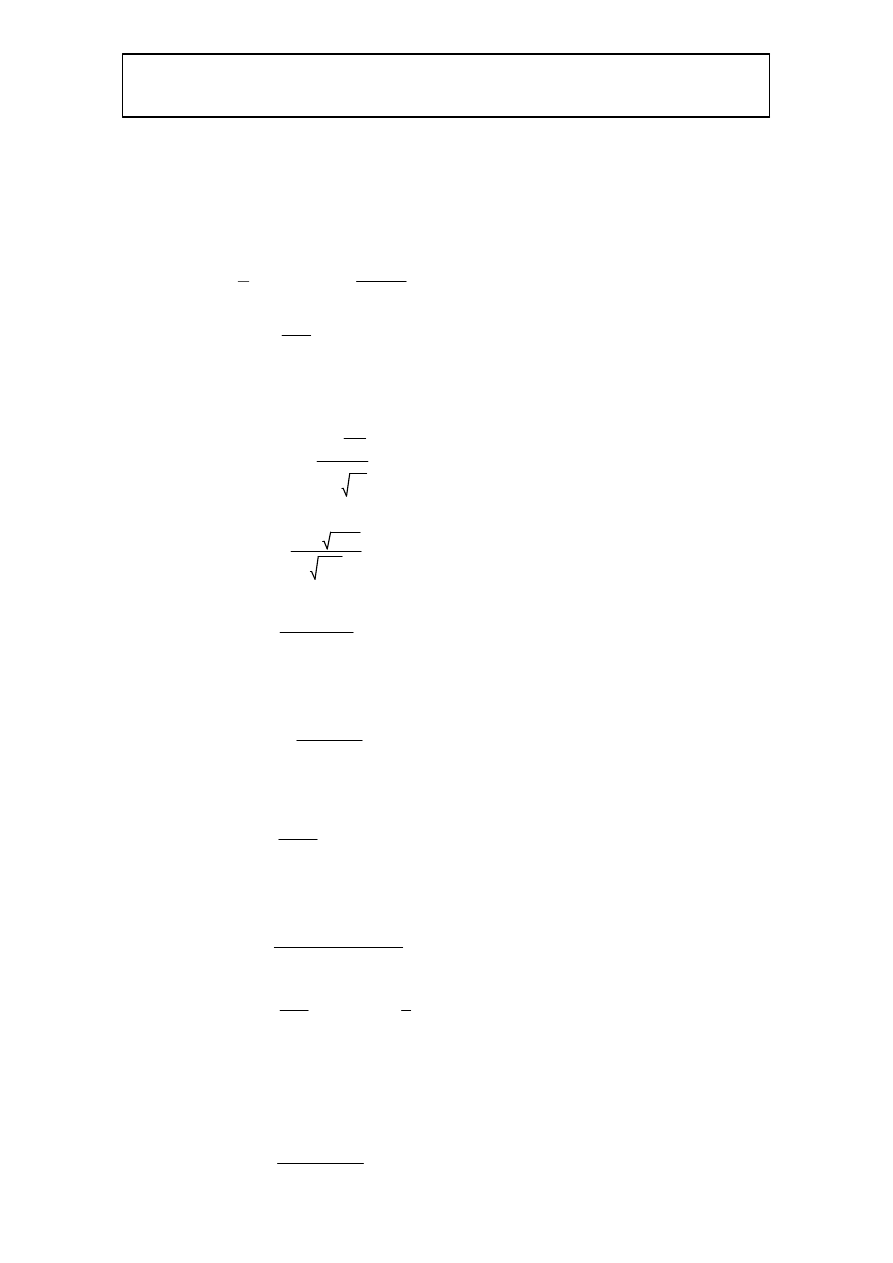
Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
Maksymalna średnica zbrojenia zgodnie z tab. D.1 wyniesie 10mm.
Zatem szerokość rys prostopadłych (przy zastosowaniu zbrojenia 6mm)
można uważać za ograniczoną do wartości w
lim
=0.3mm.
b) ugięcie
L
f
47920.7
=
L
f
f
269.07
47920.7
=
f
5.615
10
3
−
×
=
Ibet
b h
3
⋅
12
=
Ibet 1.44 10
4
×
cm
4
⋅
=
h0
120
=
RH
50%
=
ΦRH
1
1
RH
1.0
−
0.1
3
h0
⋅
+
=
ΦRH 2.014
=
fcm
fck 8MPa
+
20 MPa
⋅
=
=
βfcm
16.8
MPa
⋅
fcm
=
βfcm 3.757
=
t0
28
=
βt0
1
0.1
t0
0.20
+
=
βt0 0.488
=
ϕns.t0
ΦRH βfcm
⋅
βt0
⋅
=
ϕns.t0 3.695
=
Ec.eff
Ecm
1
ϕns.t0
+
=
Ec.eff 5.751 10
3
×
MPa
⋅
=
Es
200GPa
=
αet
Es
Ec.eff
=
αet 34.777
=
x1
0.5 b
⋅
h
2
⋅
αet As1
⋅
d
⋅
+
b h
⋅
αet As1
⋅
+
=
x1 6.23 cm
⋅
=
I1
b h
3
⋅
12
b h
⋅
x1
h
2
−
2
⋅
+
αet As1
⋅
d
x1
−
(
)
2
⋅
+
=
I1 1.556 10
4
×
cm
4
⋅
=
Bns
Ec.eff I1
⋅
894.818 kN m
2
⋅
⋅
=
=
a
f
Ecm Ibet
⋅
1
⋅
cm
Bns
⋅
=
a
0.024 cm
⋅
=
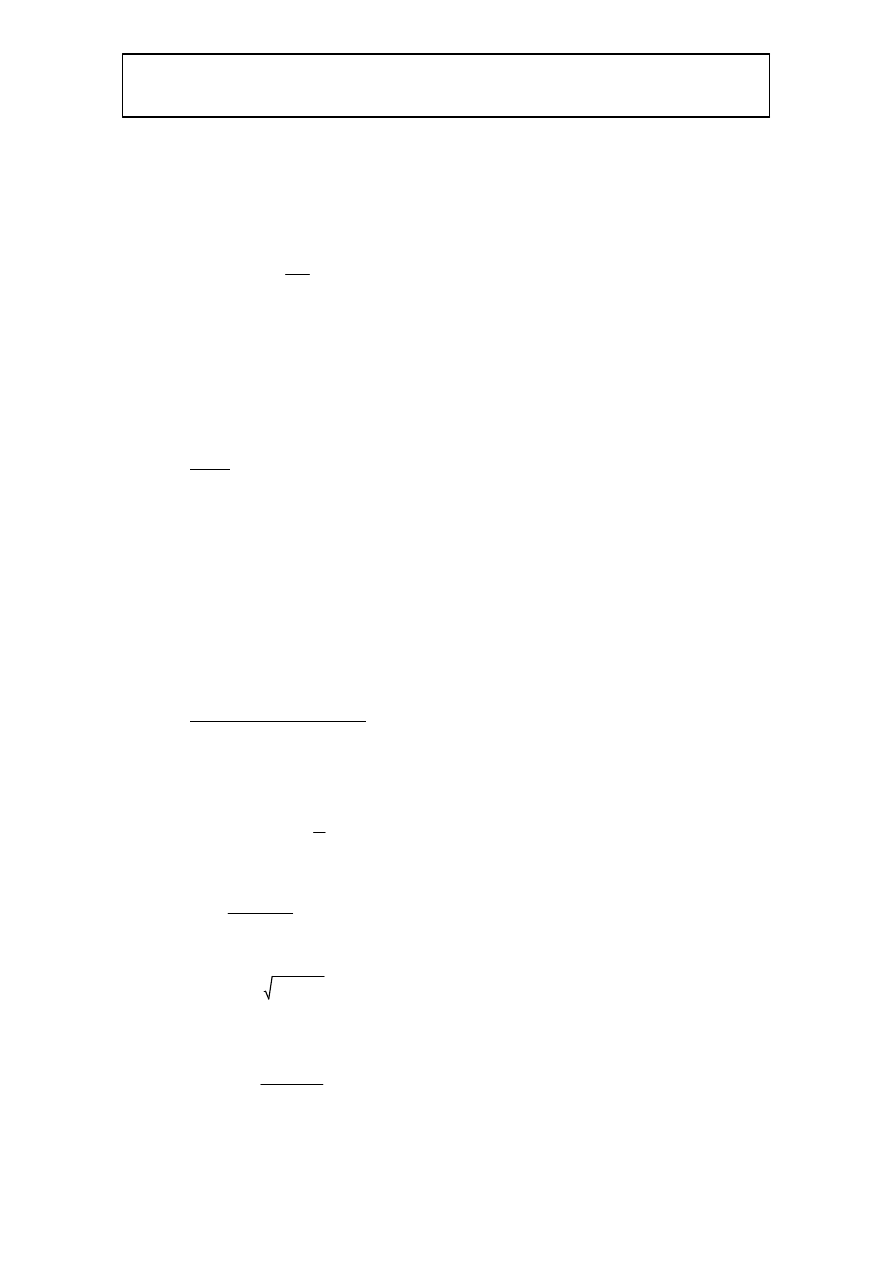
Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
Ugięcie dopuszczalne:
leff
269.07cm
=
alim
leff
200
=
alim 1.345 cm
⋅
=
a
alim
<
Warunek spełniony.
2. Płyta spocznikowa (1)
Płytę spocznikową projektuję, jako płytę jednokierunkowo zginaną.
Dane:
dane betonu i stali podane na początku
•
wymiary przekroju:
•
h
8cm
=
b
100cm
=
ś
rednica zbrojenia:
•
ϕ
6mm
=
klasa ekspozycji
•
X0 - brakryzyka korozji lub agresji środowiska
otulina
•
cmin
10mm
=
∆c
5mm
=
Stan graniczny nośności:
a) zbrojenie główne
Msd
4.859 kN
⋅
m
⋅
=
a1
cmin ∆c
+
ϕ
2
+
=
a1 0.018m
=
d
h
a1
−
=
d
0.062 m
=
sb
Msd
α fcd
⋅
b
⋅
d
2
⋅
=
sb 0.158
=
ξeff
1
1
2 sb
⋅
−
−
=
ξeff 0.173
=
< ξeff.lim 0.55
=
ζeff
1
0.5
ξeff
⋅
−
=
ζeff 0.914
=
As1.req
Msd
ζeff d
⋅
fyd
⋅
=
As1.req 2.767 cm
2
⋅
=

Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
minimalne pole zbrojenia
•
1.
As.min1
0.0013 b
⋅
d
⋅
=
As.min1 0.806 cm
2
⋅
=
2.
As.min2
0.26 b
⋅
d
⋅
fctm
fyk
⋅
=
As.min2 0.727 cm
2
⋅
=
3.
kc
0.4
=
k
0.8
=
fct.eff
fctm
=
σs.lim
400 MPa
⋅
=
Pole A
ct
rozciąganej strefy prostokątnego przekroju elementu
ż
elbetowego przy zginaniu oblicza się ze wzoru:
Act
0.5 b
⋅
h
⋅
=
Act 0.04 m
2
=
As.min3
kc k
⋅
fct.eff
⋅
Act
σs.lim
⋅
=
As.min3 0.512 cm
2
⋅
=
Minimalne pole zbrojenia wynosi:
max As.min1 As.min2
,
As.min3
,
(
)
0.806 cm
2
⋅
=
rozstaw
•
As.ϕ6
0.28cm
2
=
sreq
As.ϕ6
As1.req
100
⋅
cm
=
sreq 10.118 cm
⋅
=
s
ϕ
≥
0.6cm
⋅
=
ϕ
s
2.0cm
≥
s
25.0cm
≤
s
1.2 h
⋅
≤
1.2 h
⋅
9.6 cm
⋅
=
sprov
6.0cm
=
As.prov
As.ϕ6 100
⋅
cm
sprov
=
As.prov 4.67 cm
2
⋅
=
przyjęto zbrojenie
•
ϕ
6 mm
⋅
=
A-I co 6cm
As1
As.prov 4.67 cm
2
⋅
=
=
b) zbrojenie rozdzielcze
As.rozdz 0.15 As.prov
⋅
≥
0.15 As.prov
⋅
0.70 cm
2
⋅
=
srozdz 30.0cm
≤
srozdz.prov
25.0cm
=

Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
As.rozdz.prov
As.ϕ6
srozdz.prov
100
⋅
cm
=
As.rozdz.prov 1.12 cm
2
⋅
=
Przyjęto zbrojenie rozdzielcze:
ϕ
6 mm
⋅
=
co 25cm
As.rozdz.prov 1.12 cm
2
⋅
=
c) zbrojenie na ścinanie
Vsd
6.834kN
=
przyjęto:
ϕl
0
=
k
1
=
VRd1
0.35 fctd
⋅
k
⋅
1.2
40
ϕl
⋅
+
(
)
⋅
b
⋅
d
⋅
=
VRd1 19.009 kN
⋅
=
Vsd VRd1
≤
υ
0.6 1
fck
250 MPa
⋅
−
=
υ
0.571
=
VRd2
0.5
υ
⋅
fcd
⋅
b
⋅
d
⋅
=
VRd2 141.658 kN
⋅
=
Vsd VRd2
≤
Jest to odcinek I rodzaju - zbrojenie na ścinanie nie jest potrzebne.
Stan graniczny użytkowania:
a) szerokość rozwarcia rys:
ukośne
•
Nie trzeba sprawdzać, bo jest to odcinek I rodzaju
prostopadłe
•
d
h
0.775
=
Zatem nie można skorzystać z metody uproszczonej.
Ac
1.00m
0.08m
+
1.08 m
=
=
u
2 1.00
⋅
m
2 m
=
=
h0
2 Ac
⋅
u
=
h
80 mm
⋅
=
RH
50%
=
ΦRH
1
1
RH
1.0
−
0.1
3
h0
⋅
+
=
ΦRH 5.873
=
fcm
fck 8MPa
+
20 MPa
⋅
=
=
βfcm
16.8
MPa
⋅
fcm
=
βfcm 3.757
=
t0
28
=
βt0
1
0.1
t0
0.20
+
=
βt0 0.488
=

Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
ϕns.t0
ΦRH βfcm
⋅
βt0
⋅
=
ϕns.t0 10.777
=
Ec.eff
Ecm
1
ϕns.t0
+
=
Ec.eff 2.293 10
3
×
MPa
⋅
=
Es
200GPa
=
αet
Es
Ec.eff
=
αet 87.238
=
x1
0.5 b
⋅
h
2
⋅
αet As1
⋅
d
⋅
+
b h
⋅
αet As1
⋅
+
=
x1 4.742 cm
⋅
=
I1
b h
3
⋅
12
b h
⋅
x1
h
2
−
2
⋅
+
αet As1
⋅
d
x1
−
(
)
2
⋅
+
=
I1 5.573 10
3
×
cm
4
⋅
=
ρ
As1
b d
⋅
=
ρ
7.527
10
3
−
×
=
xII
d
ρ αet
⋅
2
αet
+
(
)
⋅
ρ αet
⋅
−
⋅
43.39 cm
⋅
=
=
III
b xII
3
⋅
3
ρ αet
⋅
b
⋅
d
⋅
d
xII
−
(
)
2
⋅
+
3.286
10
6
×
cm
4
⋅
=
=
W
b h
2
⋅
6
=
W
1.067
10
3
×
cm
3
⋅
=
Mcr
W fcm
⋅
21.333 kN m
⋅
⋅
=
=
Msd.k
3.758kN m
⋅
=
Msd.k Mcr
<
Przekrój się nie zarysuje.
b) ugięcie
L
f
70653.4
=
L
f
f
150.0
70653.4
=
f
2.123
10
3
−
×
=
Ibet
b h
3
⋅
12
=
Ibet 4.267 10
3
×
cm
4
⋅
=
Bns
Ec.eff I1
⋅
127.755 kN m
2
⋅
⋅
=
=
a
f
Ecm Ibet
⋅
1
⋅
cm
Bns
⋅
=
a
0.019 cm
⋅
=
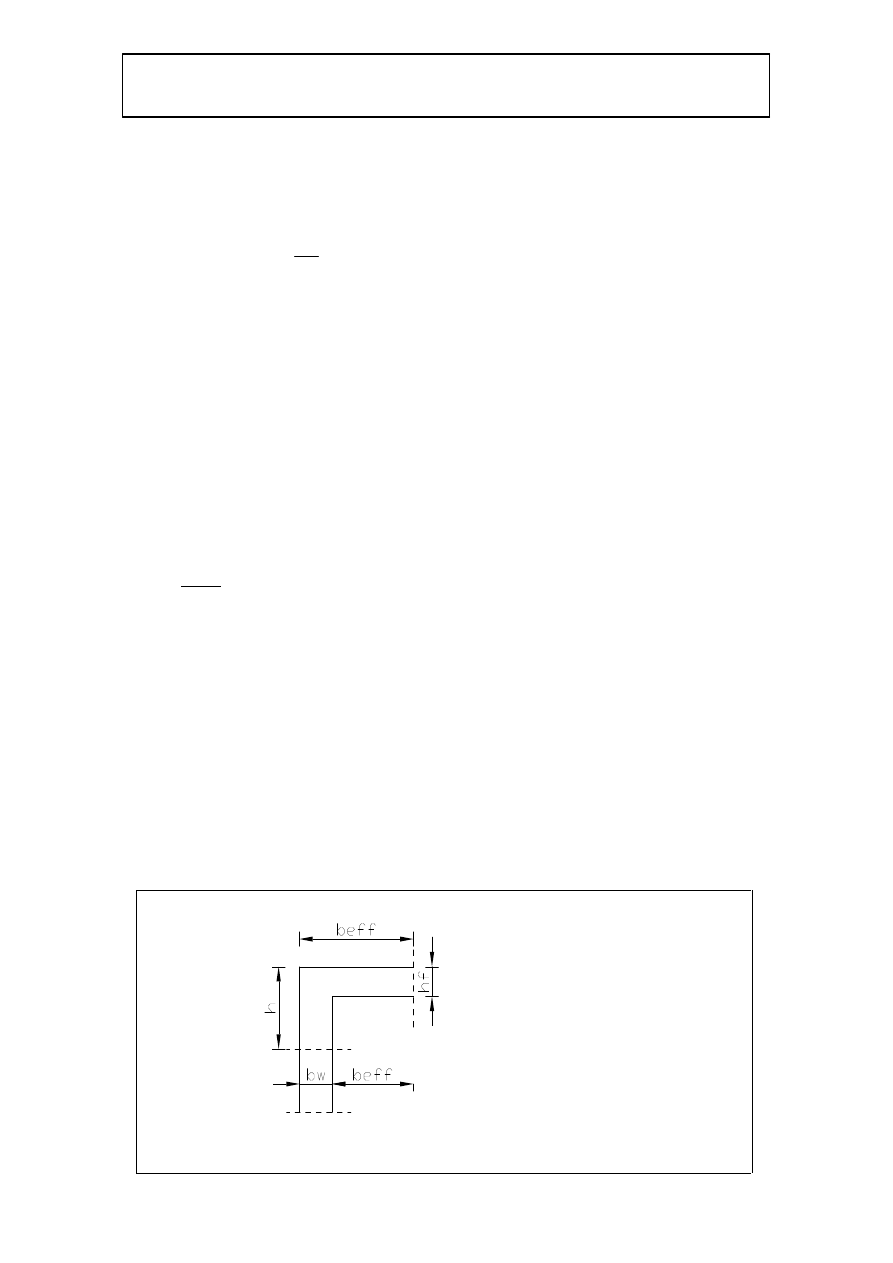
Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
Ugięcie dopuszczalne:
leff
150.0cm
=
alim
leff
200
=
alim 0.75 cm
⋅
=
a
alim
<
Warunek spełniony.
3. Płyta spocznikowa (2)
Projektuję tą płytę jako płytę dwukierunkowo zginaną.
Ze wzgłedu na to, że momenty w tej płycie są mniejsze od momentów występujących w
płycie spocznikowej (1) zdecydowałem się przyjąć zbrojenie na obu kierunkach zginania
takie same jak w płycie spocznikowej (1), jedynie z tą różnicą, że co drugi pręt przy
podporze zostanie odgięty do góry ze względu na możliwośc wystąpienia momentu
wynikającego z częściowego utwierdzenia.
4. Belka spocznikowa
Dane:
dane betonu i stali podane na początku
•
wymiary przekroju:
•
h
40cm
=
bw
20cm
=
hf
8cm
=
ś
rednica zbrojenia:
•
ϕ
22mm
=
klasa ekspozycji
•
X0 - brakryzyka korozji lub agresji środowiska
otulina
•
cmin
10mm
=
∆c
5mm
=

Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
l0
150cm
20cm
+
1.7 m
=
=
beff 4 hf
⋅
≤
,
4 hf
⋅
0.32 m
=
beff
bw
l0
10
+
0.37 m
=
=
Przyjęto:
beff
32cm
=
Najwiekszy obliczeniowy moment zginający dodatni (przyjęto schemat belki swobodnie
podpartej):
Msd
0.125 qzmienne.bs qstałe.bs
+
(
)
⋅
l0
2
⋅
=
Msd 5.886 kN m
⋅
⋅
=
Stan graniczny nośności:
a) zbrojenie główne
Msd 5.886 kN m
⋅
⋅
=
a1
cmin ∆c
+
ϕ
2
+
=
a1 0.026m
=
d
h
a1
−
=
d
0.374 m
=
Mf
α fcd
⋅
beff
⋅
hf
⋅
d
0.5 hf
⋅
−
(
)
⋅
=
Mf 68.403 kN m
⋅
⋅
=
Przekrój pozornie teowy.
sb
Msd
α fcd
⋅
beff
⋅
d
2
⋅
=
sb 0.016
=
ξeff
1
1
2 sb
⋅
−
−
=
ξeff 0.017
=
< ξ
eff.lim
0.55
=
ζeff
1
0.5
ξeff
⋅
−
=
ζeff 0.992
=
As1.req
Msd
ζeff d
⋅
fyd
⋅
=
As1.req 0.512 cm
2
⋅
=
minimalne pole zbrojenia
•
1.
As.min1
0.0013 b
⋅
d
⋅
=
As.min1 4.862 cm
2
⋅
=
2.
As.min2
0.26 b
⋅
d
⋅
fctm
fyk
⋅
=
As.min2 4.383 cm
2
⋅
=
3.
kc
0.4
=
k
0.8
=
fct.eff
fctm
=
σs.lim
400 MPa
⋅
=
Pole A
ct
rozciąganej strefy prostokątnego przekroju elementu
ż
elbetowego przy zginaniu oblicza się ze wzoru:
Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
Act
0.5 b
⋅
h
⋅
=
Act 0.2 m
2
=
As.min3
kc k
⋅
fct.eff
⋅
Act
σs.lim
⋅
=
As.min3 2.56 cm
2
⋅
=
Minimalne pole zbrojenia wynosi:
As1.req
max As.min1 As.min2
,
As.min3
,
(
)
4.86 cm
2
⋅
=
=
przyjęto zbrojenie
•
2
ϕ
22 mm
⋅
=
A-I A
s1.prov
2 3.80
⋅
cm
2
7.60 cm
2
⋅
=
=
b) zbrojenie na ścinanie
Vsd
0.5 qzmienne.bs qstałe.bs
+
(
)
⋅
l0
⋅
13.849 kN
⋅
=
=
przyjęto:
ϕl
0
=
k
1
=
VRd1
0.35 fctd
⋅
k
⋅
1.2
40
ϕl
⋅
+
(
)
⋅
bw
⋅
d
⋅
=
VRd1 22.934 kN
⋅
=
Vsd VRd1
≤
υ
0.6 1
fck
250 MPa
⋅
−
=
υ
0.571
=
VRd2
0.5
υ
⋅
fcd
⋅
bw
⋅
0.9
⋅
d
⋅
=
VRd2 153.813 kN
⋅
=
Vsd VRd2
≤
Warunek został spełniony.
s
0.75 d
⋅
≤
0.75 d
⋅
28.05 cm
⋅
=
s
40.cm
≤
s
5cm
≥
Przyjmuję rozstaw strzemion:
s
25cm
=
c) zakotwienie prętów zbrojenia głównego
podstawowa długość zakotwienia
•
fbd
1.6MPa
=
lb
ϕ
4
fyd
fbd
⋅
=
lb 106.56 cm
⋅
=

Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
obliczeniowa długość zakotwienia
•
αa
1.00
=
lbd
αa lb
⋅
As1.req
As1.prov
⋅
=
lbd 68.17 cm
⋅
=
lb.min
0.3 lb
⋅
32 cm
⋅
=
=
lb.min
10
ϕ
⋅
cm
⋅
=
=
lb.min
10cm
=
Przyjęto:
lbd 68 cm
⋅
=
Stan graniczny użytkowania:
a) szerokość rozwarcia rys:
ukośne
•
Nie trzeba sprawdzać, bo jest to odcinek I rodzaju
prostopadłe
•
d
h
0.935
=
Zatem można skorzystać z metody uproszczonej (zał. D PN).
Stopień zbrojenia:
ρ1
As1.prov
bw d
⋅
100
⋅
=
ρ1 1.02
=
zatem
ζ
0.80
=
σs
Msd
ζ d
⋅
As1.prov
⋅
=
σs 25.9 MPa
⋅
=
Maksymalna średnica zbrojenia zgodnie z tab. D.1 wyniesie 32mm.
Zatem szerokość rys prostopadłych (przy zastosowaniu zbrojenia
22mm) można uważać za ograniczoną do wartości w
lim
=0.3mm.
b) ugięcie
Korzystam z metody uproszczonej.
l0 6.00m
≤
(l
eff
/d)
max
=18
alim
leff
200
=
δ1
200
alim
leff
⋅
=
δ1 1
=
Msd.k
4.576kN m
⋅
=

Obliczenia
statyczno-wytrzmałościowe
schodów
Mateusz Janion
σs
Msd.k
δ1 d
⋅
As1.prov
⋅
=
σs 16.099 MPa
⋅
=
δ2
250MPa
σs
=
δ2 15.529
=
δ3
1.000
=
leff
d
4.011
=
<
18
δ1
⋅
δ2
⋅
δ3
⋅
279.519
=
Warunek został spełniony, zatem wartość ugięcia "a" można uważać za
ograniczoną do odpowiedniej wartości a
lim
=0.3mm.
Wyszukiwarka
Podobne podstrony:
pdf, Mathcad sciana oporowa
pdf Mathcad, dzwigar
pdf Mathcad, Zbrojenie silosa
pdf Mathcad, silos napory
pdf, Mathcad dzwigar
pdf, Mathcad Zbrojenie silosa
Mathcad Schody tuuu id 287191
Mathcad Projekt Schody druk
Mathcad, Projekt Schody druk
Mathcad sprezone kolokwium 03 06 11 gr2 pdf
schody 2
instr 2011 pdf, Roztw Spektrofoto
(ebook PDF)Shannon A Mathematical Theory Of Communication RXK2WIS2ZEJTDZ75G7VI3OC6ZO2P57GO3E27QNQ
KSIĄŻKA OBIEKTU pdf
Mathcad przepona kotwiczna projekt 2
zsf w3 pdf
więcej podobnych podstron