c.d. mediacji i moderacji
oraz wnioskowanie
indukcyjne

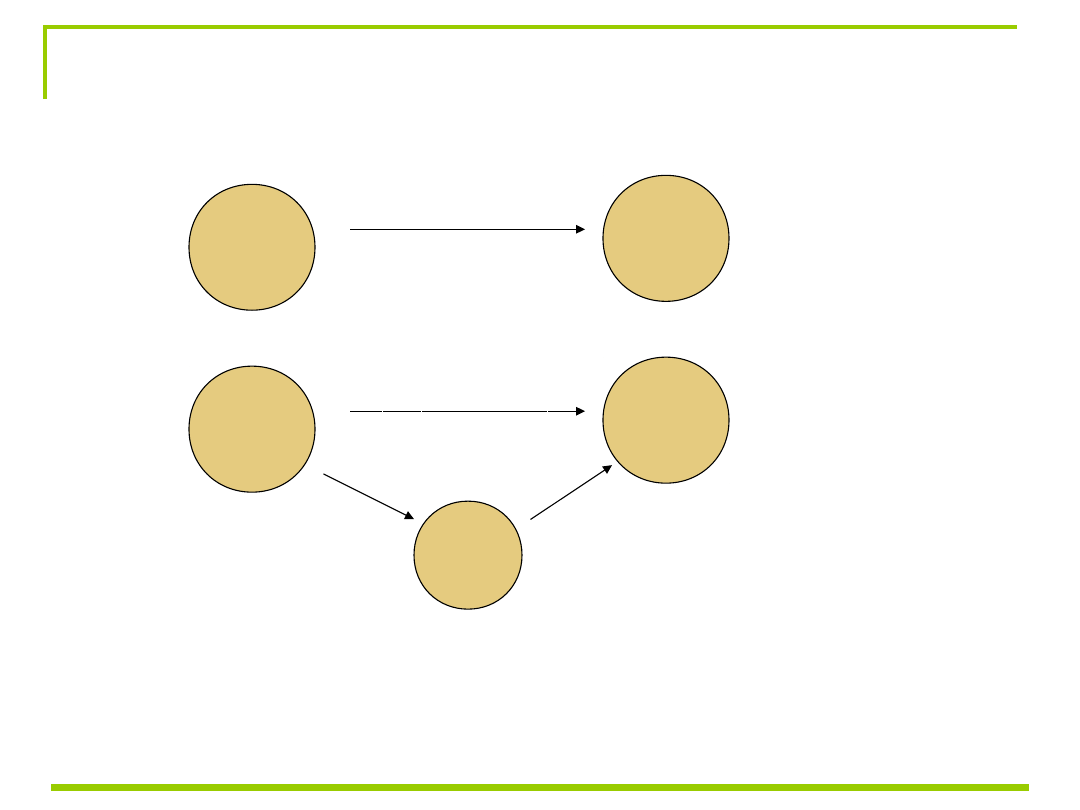
Pamięć operacyjna jako mediator
zależności między wiekiem a uwagą

1. Istotny związek między mediatorem z zmienną zależną
2. Istotny związek między predyktorem a mediatorem
3. Pierwotny związek między predyktorem a zmienną zależną
staje się nieistotny lub ulega istotnemu osłabieniu

Wiek

Pamięć

Uwaga

*

*

Wiek

Uwaga

*



Przykład procedury

eksperymentalnej

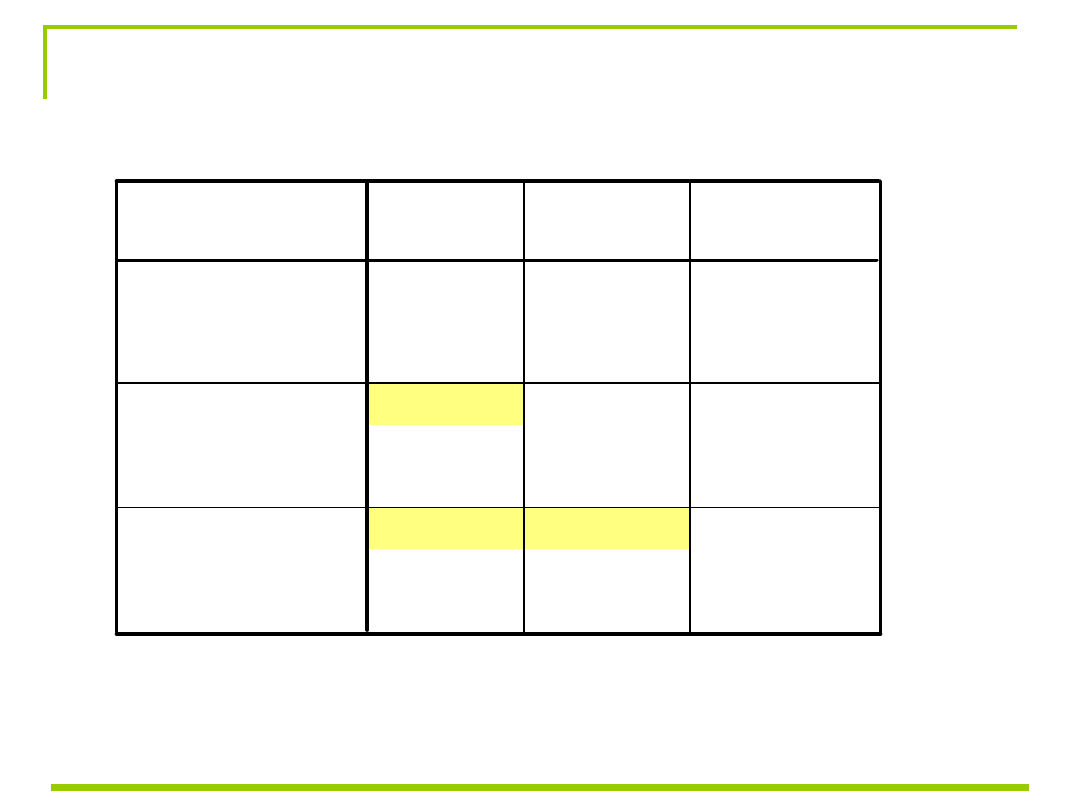
Correlations

-,813**

,000

25

-,735**

,857**

,000

,000

25

25

wiek

pamiec

uwaga_pop

wiek

pamiec

uwaga_

pop

Correlation is significant at the 0.01 level

(2-tailed).

**.

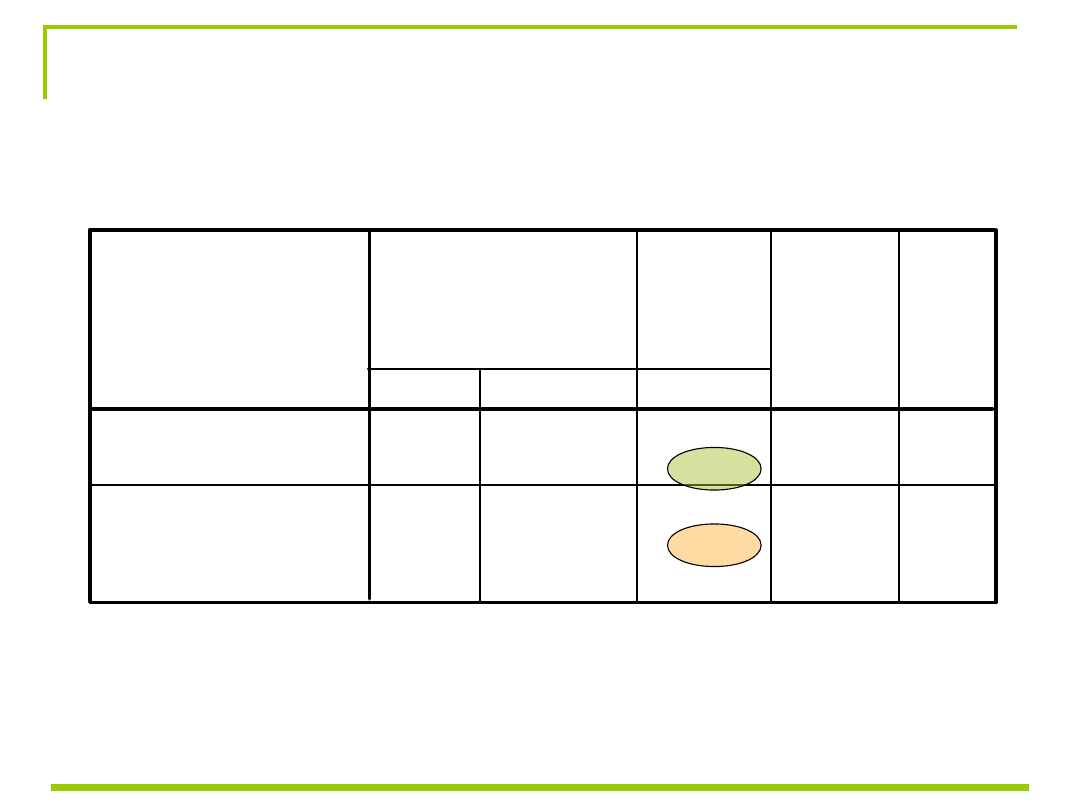
Coefficients

a

9,276

,869

10,678 ,000

-,105

,020

-,735 -5,192 ,000

-,437

2,467

-,177 ,861

-,016

,027

-,111

-,592 ,560

,159

,039

,767

4,090 ,000

(Constant)
wiek
(Constant)
wiek
pamiec

Model
1

2

B

Std. Error

Unstandardized

Coefficients

Beta

Standar

dized

Coeffici

ents

t

Sig.

Dependent Variable: uwaga_pop

a.

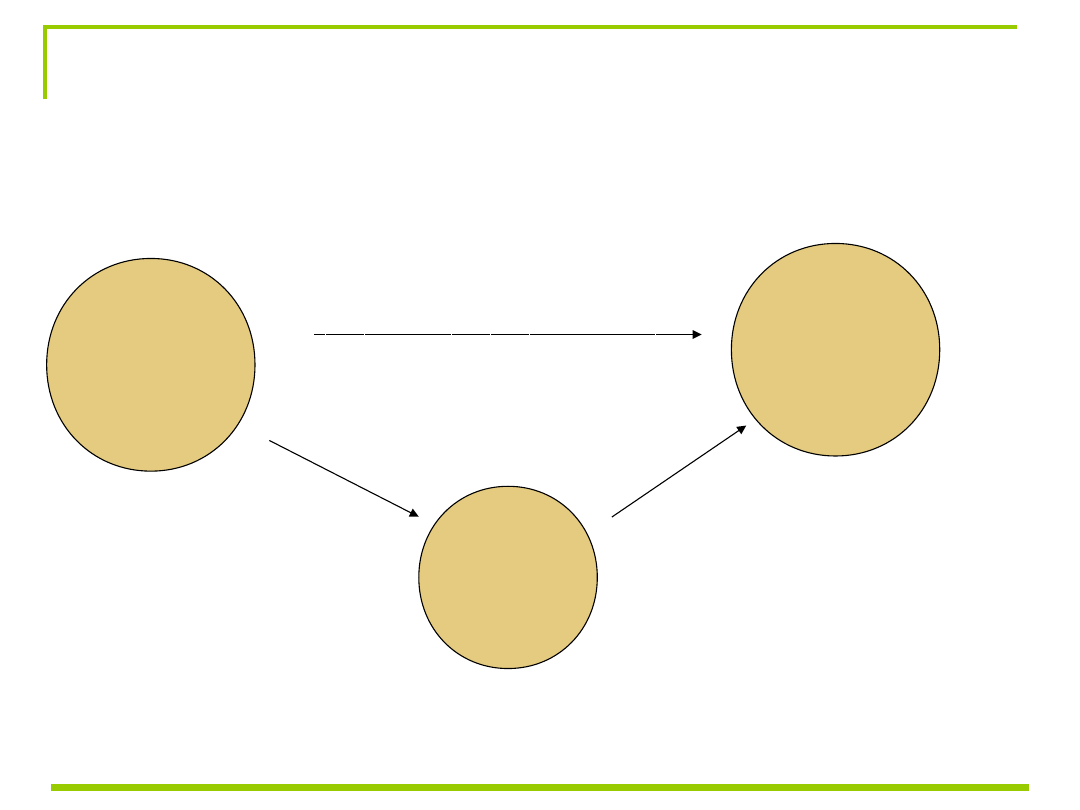
Siła pierwotnej zależności po
uwzględnieniu mediatora

Wiek

Pamięć

Uwaga

***

-0,81

***

-0,78

-0,11; ni

Rozwiązywanie sylogizmów
przez osoby depresyjne i
niedepresyjne



Sylogizmy wiarygodne



Dotyczą wniosków na temat normalnego
ogrodu



Sylogizmy niewiarygodne



Dotyczą wniosków na temat ogrodu
genetycznego



Dodatkowo miara pojemności pamięci
operacyjnej

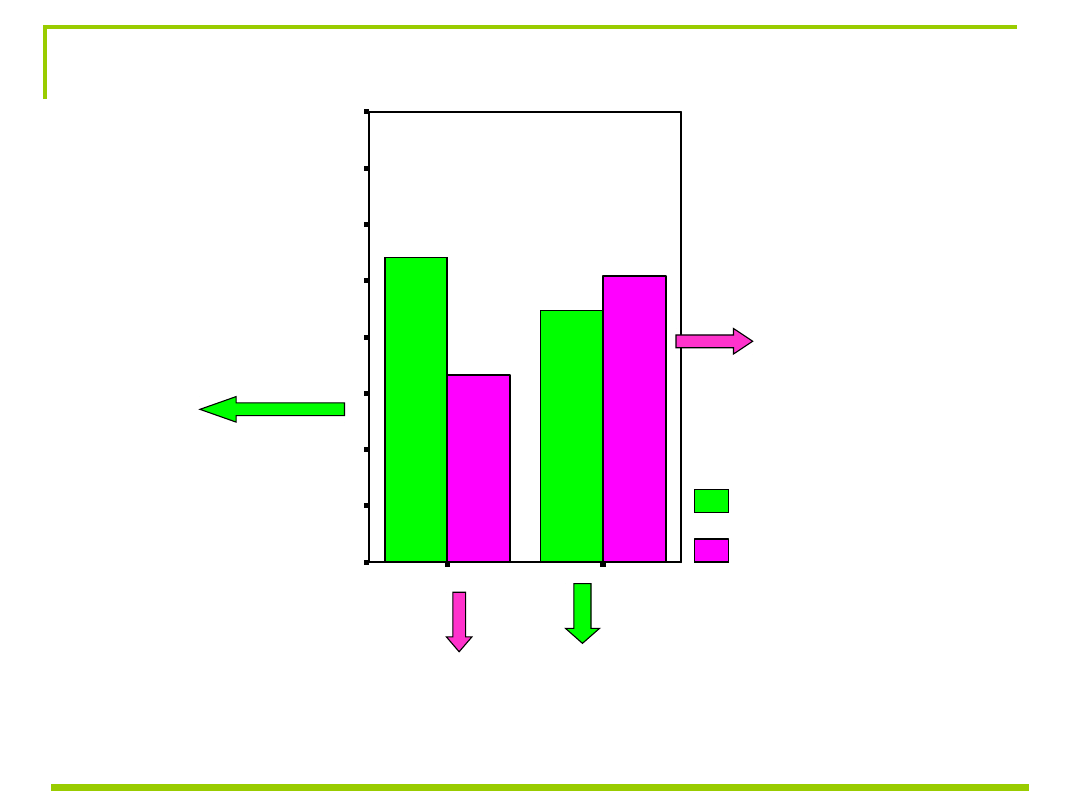
konkluzje

nieprawdziwe

prawdziwe

P

op

ra

w

no

ść

1,0

,9

,8

,7

,6

,5

,4

,3

,2

ogród normalny

ogród genetyczny

Przesłanki:
Wszystkie śliwki
mają pestki.
Wszystkie mirabelki
to śliwki.
Konkluzja:
Wszystkie mirabelki
mają pestki.

Przesłanki:
Niektóre wiśnie są słodkimi
owocami.
Wszystkie słodkie owoce mają
lepiące się nóżki.
Konkluzja:
Niektóre wiśnie mają lepiące się
nóżki.

Przesłanki:
Wszystkie brzoskwinie są delikatne.
Niektóre delikatne owoce są pyszne.
Konkluzja:
Niektóre brzoskwinie są pyszne.

Przesłanki:
Niektóre kwiaty są żółte.
Wszystkie słyszące rośliny
są kwiatami.
Konkluzja:
Niektóre słyszące rośliny są
żółte

Wyniki:

Wiarygodność x prawdziwość:

F(1,111) = 45,10 p < 0,001

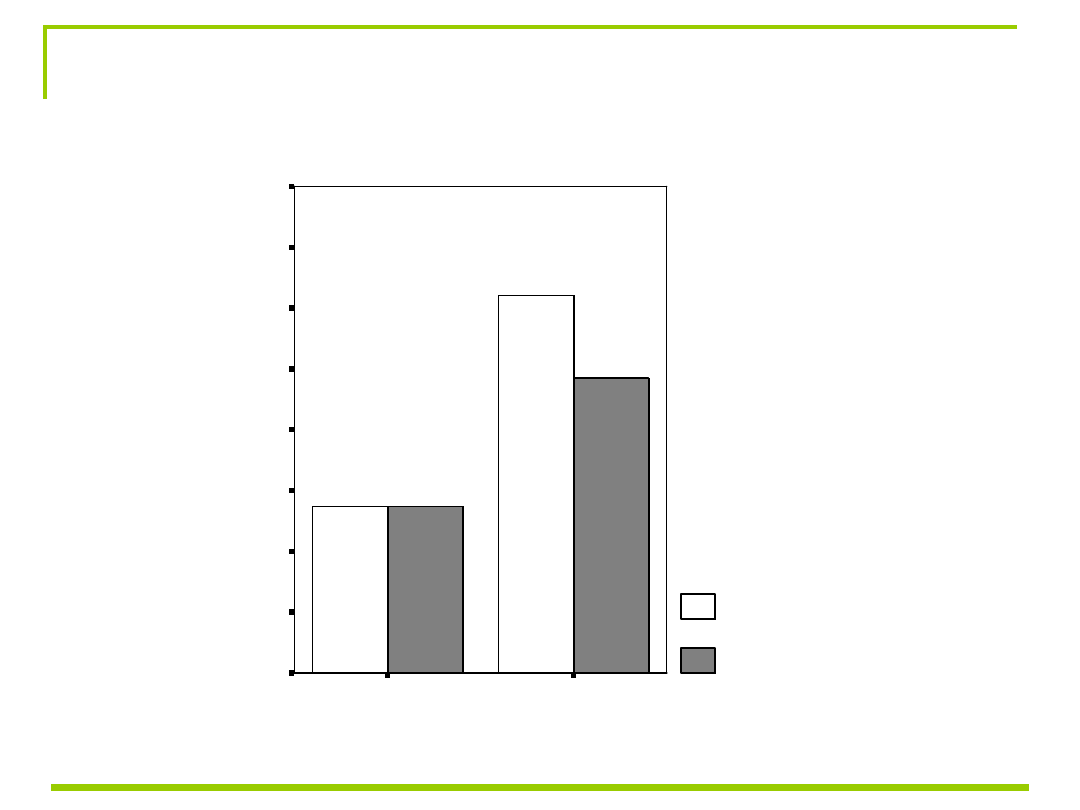
Interakcja Depresji i Pamięci (moderator)

Sylogizmy trudniejsze (3 M)

RSPAN

wysoka WMC

niska WMC

po

pr

aw

no

ść

1,0

,9

,8

,7

,6

,5

,4

,3

,2

niedepresyjni

depresyjni

Hipotezy

Testowanie hipotez i
istotność statystyczna



Stawiamy hipotezy



o różnicy między warunkami eksperymentalnymi.



o związkach między zmiennymi.



Zbieramy dane na ich poparcie



Jakie jest prawdopodobieństwo, że uzyskany przez nas

związek między zmiennymi, czy różnica jest dziełem

przypadku, błędu próbkowania?



Im mniejsze to prawdopodobieństwo, tym bardziej pewni

jesteśmy, wniosku o występowaniu rzeczywistych różnic

na poziomie populacji

Etapy testowania hipotez



Stawiamy hipotezę badawczą



Zbieramy dane



Stawiamy hipotezę zerową



Konstruujemy rozkład

prawdopodobieństwa otrzymania takiego

wyniku przy założeniu, że hipoteza zerowa

jest prawdziwa



Porównujemy wynik uzyskany z rozkładem



Znajdujemy prawdopodobieństwo uzyskania

takiego wyniku



Podejmujemy decyzję o odrzuceniu bądź

nie hipotezy zerowej.

Hipoteza zerowa; H

0



Dlaczego stawiamy hipotezę, która jest
zaprzeczeniem tego, co chcemy
udowodnić?



Ponieważ nigdy nie możemy udowodnić, że
coś jest prawdą, ale możemy wykazać, że
coś jest fałszem



Jest punktem wyjścia dla każdego testu
statystycznego

Hipoteza badawcza; H

1



Hipoteza stawiana przez badacza



Najlepsze z możliwych wytłumaczeń

obserwowanego zjawiska w przypadku, kiedy

hipoteza zerowa jest fałszywa.



W badaniach staramy się potwierdzić naszą

hipotezę badawczą, alternatywną.



Jednakże z metodologicznego punktu widzenia nie

jest możliwe, aby w pełni udowodnić jej

prawdziwość



Wystarczy, że pojawi się jeden przypadek

zaprzeczający hipotezie i staje się ona fałszywa

(odnosi się to również do teorii).

Hipotezy badawcze,
alternatywne

•

Niekierunkowa

Niekierunkowa



Nie twierdzi nic o kierunku zależności czy
różnicy



Trudniejsze do przyjęcia statystycznie



Wykorzystuje się dwustronne testy statystyczne

•

Kierunkowa

Kierunkowa



Explicite określa kierunek zależności czy różnicy



Hipotezy te są łatwiejsze do przyjęcia
statystycznie



Wykorzystuje się jednostronne testy
statystyczne

2

1

0

:







H

2

1

1

:







H

2

1

1

:







H

2

1

1

:







H

lub

HIPOTEZA ZEROWA

HIPOTEZA ZEROWA

HIPOTEZY ALTERNATYWNE

HIPOTEZY ALTERNATYWNE

NIEKIERUNKOWA

NIEKIERUNKOWA

KIERUNKOWE

KIERUNKOWE

0

:

2

1

1









H

0

:

2

1

0









H

0

:

2

1

1









H

0

:

2

1

1









H

lub

Tropiciele usterek

Kolory emocji



HIPOTEZA



Kolor niesie w sobie ładunek emocjonalny a jego

ocena (pozytywna vs. negatywna) nie zależy od

rodzaju bodźca afektywnego poprzedzającego

bodziec kolorystyczny.



Badanie eksperymentalne z dwiema grupami

eksperymentalnymi i jedną grupą kontrolną z

planem dla grup niezależnych.



Zmienna niezależna: rodzaj ekspozycji (pozytywna,

negatywna lub jej brak)



Zmienna zależna: kategoryzacja kolorów

(pozytywne, negatywne, neutralne)



Zmienne kontrolowane: standaryzacja procedury

oraz randomizacja

Efekt sprężyny: Paradoksalne skutki sztucznej
poprawności politycznej



posiadanie lub brak negatywnego
stereotypu Rumuna,



tłumienie negatywnych,
stereotypowych myśli o Rumunie.



ustosunkowanie do Rumuna

Przebieg badania



badani oceniali Rumuna na skalach, na których zostało

umieszczone 10 par przeciwległych przymiotników

(dyferencjał semantyczny).



zdjęcie Rumuna, a zadaniem badanych było opisanie jak

wyobrażają sobie jego typowy dzień. Połowa badanych

dostała jednak polecenie, w którym była zawarta prośba by

opisując Rumuna nie myśleli(-ały) o nim w sposób

stereotypowy.



osoby badane otrzymały trzy zadania.



badani wskazywali miejsce w klasie, na którym chcieliby

usiąść wśród osób innych narodowości - w tym Rumuna

(zarówno osoby jak i obszar klasy były na kartce

oznaczone).



opis kolejnego Rumuna ze zdjęcia



dyferencjał semantyczny..



Odnotowano istotną i zgodną z kierunkiem
hipotezy różnicę w ilości stereotypowych,
negatywnych myśli o Rumunie między opisami.



W drugim opisie nastąpił wyraźny wzrost negatywnych
myśli.



Na podstawie testu t dla grup zależnych obliczyliśmy, że
wzrost ten wynosił ponad 52% (t=-4,286, df=7) i był
istotny na poziomie istotności p < 0,01.



Dla porównania w grupie kontrolnej liczba stereotypowych
myśli w opisie pierwszym i drugim nie różniła się ze sobą
istotnie. Na podstawie tej analizy można więc powiedzieć,
że zaszedł oczekiwany efekt sprężyny.

Wpływ tłumienia myśli o pozytywnie
stereotypizowanej kategorii społecznej
na ustosunkowanie do tej kategorii



Hipoteza teoretyczna



Tłumienie pozytywnych myśli stereotypowych o obiekcie

spowoduje zmianę postawy wobec tego obiektu.



Hipoteza badawcza



Tłumienie myśli pozytywnych o osobie posiadającej

autorytet spowoduje u osoby o pozytywnym stereotypie

zmianę na negatywniejszą postawę.



Operacjonalizacja zmiennych



Zmienna zależna - zmiana postawy wobec

stereotypizowanej kategorii społecznej lub też brak takiej

zmiany.



Wskaźnikiem tego będzie liczba określeń o zabarwieniu

emocjonalnym wobec osoby GOPR-owca, ustalona przez sędziów

niezależnych



Zmienna niezależna - polecenie tłumienia vs brak takiego

polecenia.



W pierwszej części badania w grupie
eksperymentalnej w której użyliśmy
zmiennej niezależnej (tłumienie)
otrzymaliśmy średnią 17,99 zaś w drugiej
części badania (bez tłumienia) średnia
wyniosła 42,95.



Wynik testu t dla prób zależnych otrzymaliśmy
następujący: t(16) -3,883; p<0,05.



DOKŁADNIEJ ISTOTNOŚĆ OTRZYMALIŚMY NA
POZIOMIE: 0,001. Wskazuje to na bardzo dużą
dokładność testu.

„Mój pierwszy szef” -
wyobrażenia i oczekiwania
studentek ostatnich lat
studiów dotyczące płci
psychologicznej przyszłego
przełożonego

Patrycja Rydel
Praca magisterska
napisana pod kierunkiem
prof. dr hab. Michała Stasiakiewicza



Badanie polegało na dwukrotnym (w odniesieniu

do siebie i w odniesieniu do przyszłego szefa)

wypełnieniu przez osoby badane “Inwentarza Płci

Psychologicznej” oraz udzieleniu odpowiedzi w

kwestionariuszu dotyczącym planów

zawodowych.



czy kobiety w zależności od natężenia własnej

kobiecości będą wybierały szefa o podobnym

natężeniu kobiecości. W tym celu

przeprowadzono test t – Studenta dla prób

zależnych. Analiza ujawniła, że są różnice w

natężeniu własnej kobiecości a kobiecości

preferowanego szefa t(151)=8,5; p<0,001

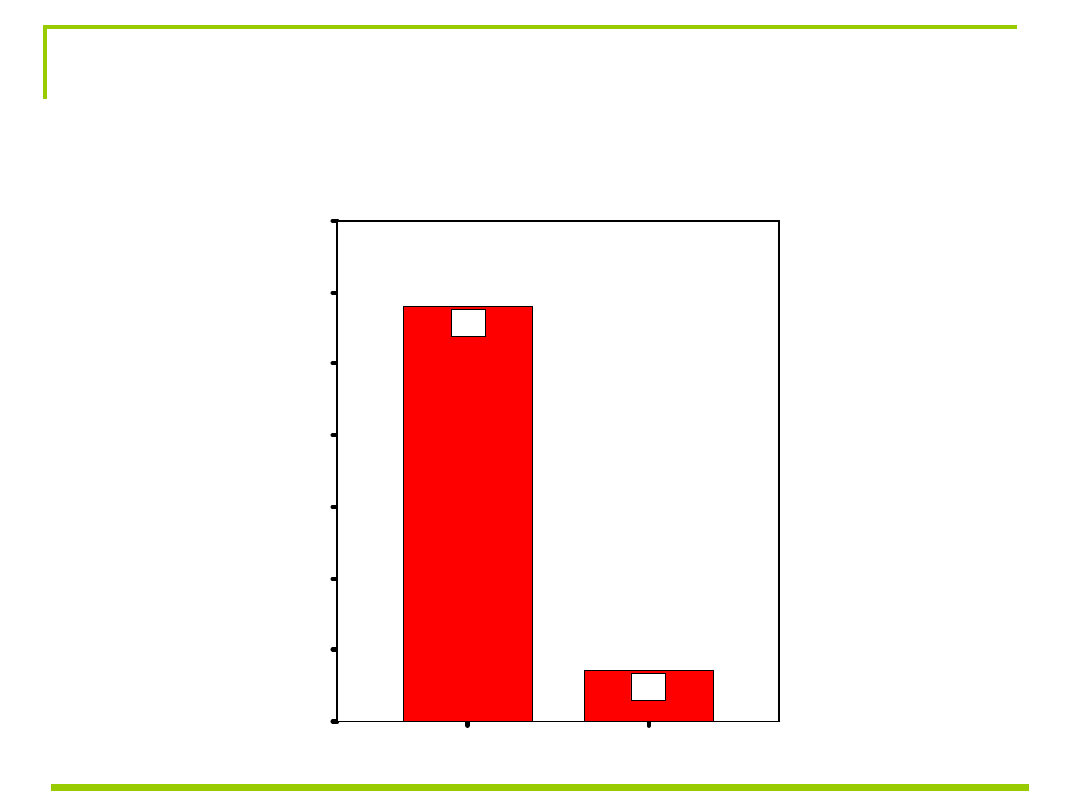
Kobiety o wysokim poziomie kobiecości
(M=54,8; SD=6,8) wybierają istotnie mniej
kobiecego szefa (M=49,7; SD=5,9) w zakresie
płci psychologicznej.

KOBIECOŚĆ SZEFA

KOBIECOŚĆ

Ś

re

dn

ia

56

55

54

53

52

51

50

49

50

55



Aby sprawdzić czy kobiety w zależności
od natężenia własnej męskości będą
wybierały szefa o podobnym natężeniu
męskości przeprowadzono test t –
Studenta dla prób zależnych. Wyniki
okazały się istotne statystycznie i
wykazały różnice w natężeniu własnej
męskości a męskości preferowanego
szefa t(151)=10,9; p<0,001

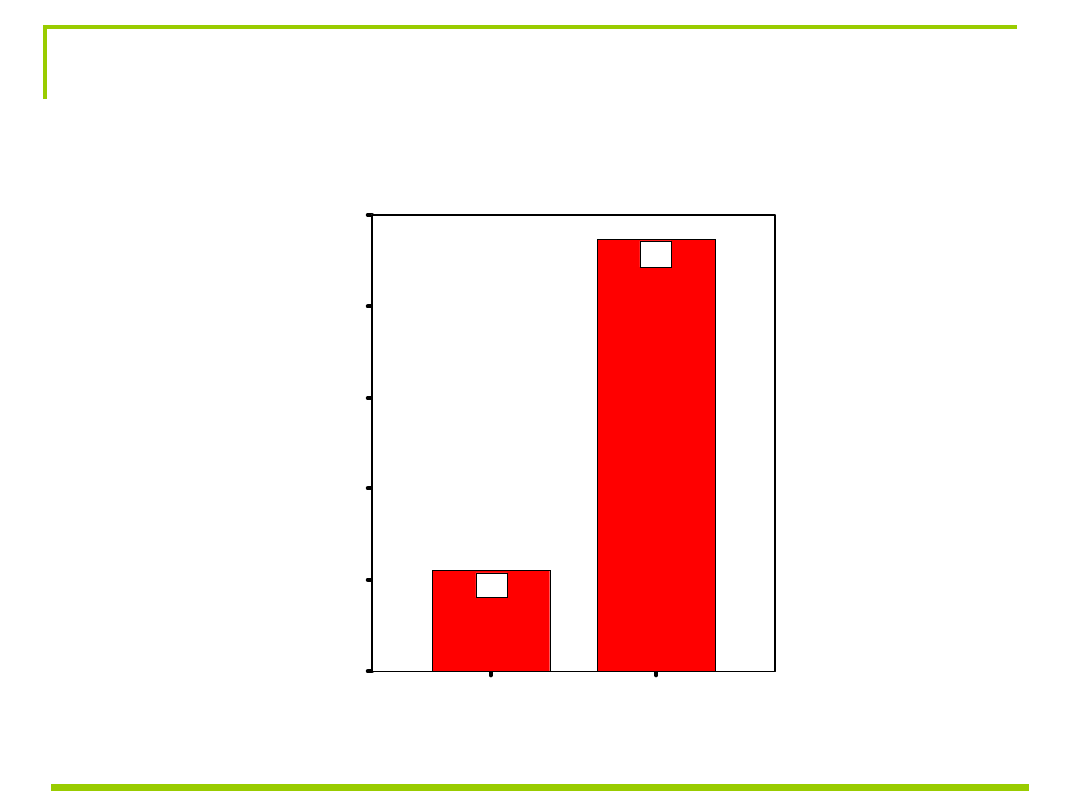
Kobiety o wysokim poziomie męskości
(M=48,2; SD=7,9) wybierają istotnie bardziej
męskiego szefa (M=55; SD=5,6) w zakresie
płci psychologicznej.

MĘSKOŚĆ SZEFA

MĘSKOŚĆ

Ś

re

dn

ia

56

54

52

50

48

46

55

48

Wnioskowanie
indukcyjne w badaniach

Podziękowania dla prof. dr hab. Andrzeja Nowaka za udostępnienie materiałów

Wnioskowanie indukcyjne



Na podstawie wielu przesłanek

jednostkowych, stwierdzających iż

poszczególne zbadane przedmioty pewnego

rodzaju mają pewną cechę, dochodzi się (przy

braku przesłanek negatywnych) do wniosku

ogólnego, że każdy przedmiot tego rodzaju

taką cechę posiada.



Metoda indukcji to metoda polegająca na

dokonywaniu obserwacji i eksperymentów,

wyprowadzaniu na ich podstawie uogólnień oraz

formułowaniu hipotez i ich weryfikacji.

Opis i wnioskowanie



Statystyka opisowa

Statystyka opisowa



Analiza danych w odniesieniu do próby np.
statystyki rozkładu wyników



Statystyka inferencyjna

Statystyka inferencyjna



Oparta o reguły wnioskowania indukcyjnego –
na podstawie uzyskanych danych wyciągamy
ogólne wnioski



Na podstawie próby wnioskujemy o populacji

Populacja

Populacja

(def.) – dowolnie

określony zespół

przedmiotów, osób,

zdarzeń, etc.

Próba

Próba

(def.) – dowolny

(def.) – dowolny

podzbiór, podgrupa

podzbiór, podgrupa

wybrany/a z populacji

wybrany/a z populacji



Statystyka opisowa – wstępny proces analizy
danych



Nie wystarcza do odpowiedzi na pytania i hipotezy,
które sobie stawiamy



Czy wyniki osób z grupy eksperymentalnej różnią
się od wyników grupy kontrolnej?



Czy różnica średniego wykonania zadania w
porównywanych grupach jest istotna statystycznie,

czy jest tylko wynikiem przypadku?



W jaki sposób wnioskować o

parametrach populacji na podstawie

badań?



Czy muszę przebadać całą populację?

Rozkład statystyki z prób

Teoretyczny rozkład średnich
z próby



Losujemy z populacji możliwie wiele

prób ze zwracaniem



Liczymy dla każdej próby średnią



Średnie te traktujemy jako dane i

obliczamy statystyki rozkładu



Średnia ze średnich z tych prób byłaby

bliska rzeczywistej średniej w populacji



Co więcej rozkład z tych prób jest bliski

normalnemu

Centralne Twierdzenie
Graniczne

Wraz ze wzrostem liczebności prób,

Wraz ze wzrostem liczebności prób,

niezależnie od kształtu rozkładu w

niezależnie od kształtu rozkładu w

populacji, rozkład z próby średnich

populacji, rozkład z próby średnich

zbliża się do normalnego ze średnią

zbliża się do normalnego ze średnią





i

i

wariancją

wariancją





2

2





Rozkład średniej z próby

Rozkład każdej

próbki opisany

przez średnią i

odchylenie

standardowe

Rozkład z próby

opisany jest również

przez średnią i

odchylenie

standardowe, które

określane jest tu

błędem

standardowym

Nasze próbki mogą być skośne, dwumodalne, a jednak rozkład średnich

z takich próbek będzie zbliżony do normalnego,

prawdopodobieństwo uzyskania danej średniej