Egzamin dla Aktuariuszy z 6 października 2008 r.
Matematyka Finansowa
Zadanie 1
i
R - rata dla i-tej transzy
25
1
100000
a
R
=
22
2
100000
a
R
R
=
−
.................
{
}
6
,...,
1
)
1
(
100000
)
1
(
3
25
∈
=
−
−
−
−
i
a
R
R
i
i
i
zadłużenie po 20 latach:
200000
...
5
6
5
2
5
1
=
+
+
+
a
R
a
R
a
R
å
å
å
=
=
−
−
−
=
÷
ø
ö
ç
è
æ
−
−
−
=
−
−
=
=
6
1
6
1
3
28
5
)
1
(
3
25
5
5
05
,
0
05
,
1
1
1
)
1
(
100000
)
1
(
100000
i
i
i
i
i
R
i
a
a
R
i
a
R
a
L
(
)
å
=
−
−
−
⋅
÷
ø
ö
ç
è
æ
−
=
−
−
1
05
,
1
05
,
1
)
1
(
100000
05
,
0
05
,
0
05
,
1
1
1
3
28
3
28
5
i
i
R
i
ê
ë
é
−
−
+
−
−
+
−
⋅
ú
ú
û
ù
ê
ê
ë
é
÷
ø
ö
ç
è
æ
−
=
1
05
,
1
05
,
1
)
2
100000
(
1
05
,
1
05
,
1
)
100000
(
1
05
,
1
05
,
1
100000
05
,
1
1
1
19
19
22
22
25
25
5
R
R
200000
1
05
,
1
05
,
1
)
5
100000
(
1
05
,
1
05
,
1
)
4
100000
(
1
05
,
1
05
,
1
)
3
100000
(
10
10
13
13
16
16
=
ú
û
ù
−
−
+
−
−
+
−
−
+
R
R
R
+
−
⋅
+
−
⋅
+
÷
ø
ö
ç
è
æ
−
−
−
⋅
=
1
05
,
1
05
,
1
100000
1
05
,
1
05
,
1
100000
05
,
1
1
1
200000
1
05
,
1
05
,
1
100000
19
19
22
22
5
25
25
A
gdzie
RB,
1
05
,
1
05
,
1
100000
1
05
,
1
05
,
1
100000
1
05
,
1
05
,
1
100000
10
10
13
13
16
16
=
−
⋅
+
−
⋅
+
−
⋅
+
1
05
,
1
05
,
1
5
1
05
,
1
05
,
1
4
1
05
,
1
05
,
1
3
1
05
,
1
05
,
1
2
1
05
,
1
05
,
1
10
10
13
13
16
16
19
19
22
22
−
⋅
+
−
⋅
+
−
⋅
+
−
⋅
+
−
=
B
6000
6028
≈
≈
=
B
A
R
Zadanie 2
A
x
- tyle procent płaci A do instytucji
B
x
- tyle procent płaci B do instytucji
F – instytucja
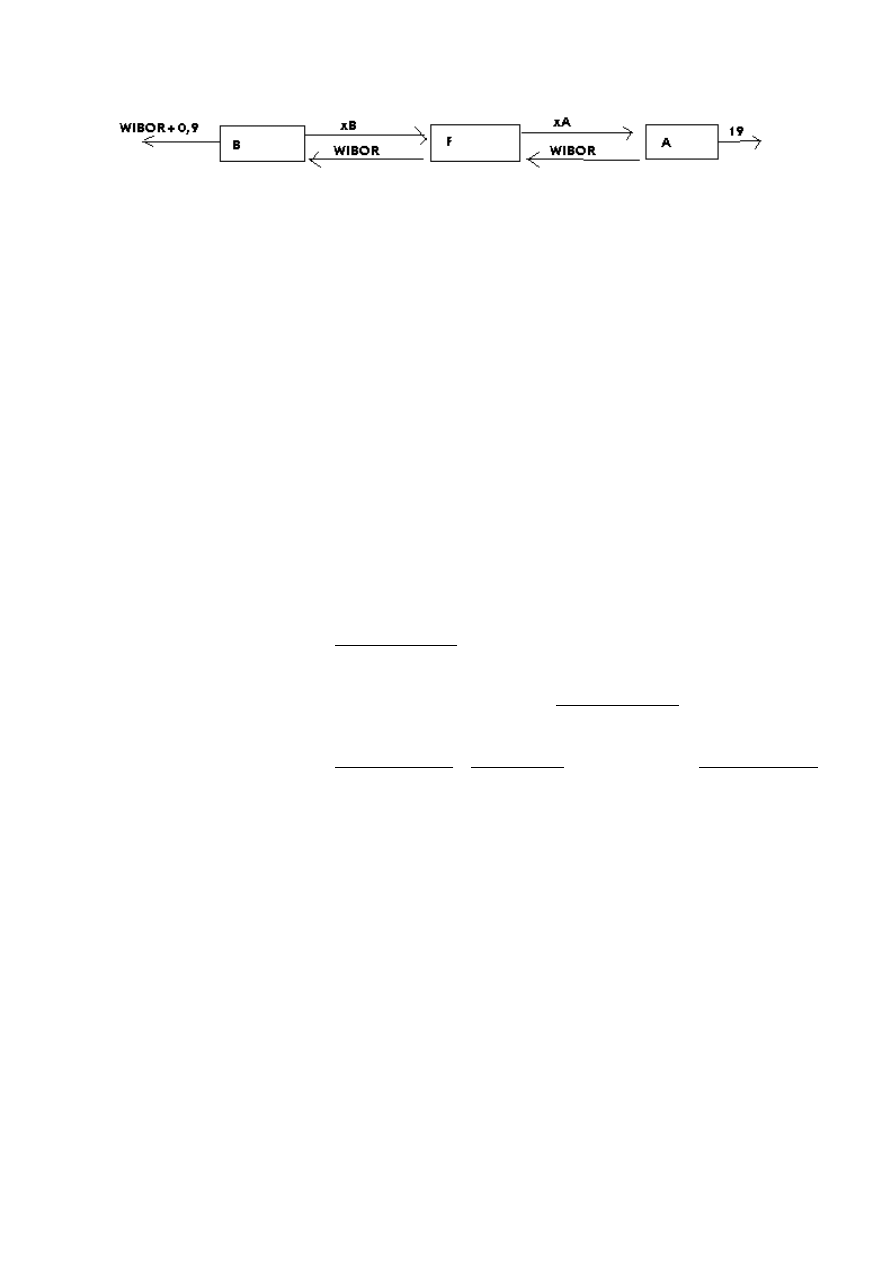
85
,
18
)
19
(
15
,
0
−
=
−
+
−
+
=
A
A
x
x
WIBOR
WIBOR
zyskA
(
)
B
B
x
WIBOR
WIBOR
x
zyskB
−
=
−
+
+
−
=
35
,
20
9
,
0
25
,
21
A
B
x
x
zyskF
−
=
î
í
ì
=
=
→
î
í
ì
−
=
−
=
−
85
,
19
35
,
19
35
,
20
85
,
18
5
,
0
B
A
B
A
A
B
x
x
x
x
x
x
75
,
20
9
,
0
85
,
19
9
,
0
=
+
=
+
=
B
x
ODP
Zadanie 3
06
,
1
50000
1
⋅
=
R
06
,
1
)
2000
06
,
1
50000
75
,
0
(
2
+
⋅
⋅
=
R
(
)
(
)
06
,
1
2000
06
,
1
75
,
0
2000
50000
06
,
1
75
,
0
06
,
1
2000
75
,
0
2
2
2
3
+
⋅
⋅
+
⋅
=
+
=
R
R
(
)
(
)
06
,
1
2000
06
,
1
75
,
0
2000
06
,
1
75
,
0
2000
50000
06
,
1
75
,
0
06
,
1
2000
75
,
0
2
2
3
3
3
4
+
⋅
⋅
+
⋅
+
⋅
=
+
=
R
R
(
)
(
2
2
3
3
4
4
4
5
06
,
1
75
,
0
2000
06
,
1
75
,
0
2000
50000
06
,
1
75
,
0
06
,
1
2000
75
,
0
⋅
+
⋅
+
⋅
=
+
=
R
R
)
06
,
1
2000
06
,
1
75
,
0
2000
+
⋅
⋅
+
.................................
(
)
[
]
=
+
+
⋅
+
+
⋅
=
−
−
−
−
06
,
1
06
,
1
75
,
0
...
06
,
1
75
,
0
1
2000
50000
06
,
1
75
,
0
2
2
1
1
i
i
i
i
i
R
(
)
06
,
1
06
,
1
75
,
0
1
06
,
1
75
,
0
1
2000
50000
06
,
1
75
,
0
1
1
1
ú
ú
û
ù
ê
ê
ë
é
⋅
−
⋅
−
+
⋅
=
−
−
−
i
i
i
(
)
å
å
=
=
−
−
−
=
ú
ú
û
ù
ê
ê
ë
é
⋅
−
⋅
−
+
⋅
⋅
=
=
25
9
25
9
1
1
1
06
,
1
75
,
0
1
06
,
1
75
,
0
1
2000
06
,
1
75
,
0
50000
06
,
1
25
,
0
25
,
0
i
i
i
i
i
i
R
ODP
(
)
(
)
(
)
(
)
≈
ú
ú
û
ù
ê
ê
ë
é
÷
÷
ø
ö
ç
ç
è
æ
⋅
−
⋅
−
⋅
−
⋅
−
+
⋅
−
⋅
−
⋅
⋅
=
06
,
1
75
,
0
1
06
,
1
75
,
0
1
06
,
1
75
,
0
17
06
,
1
75
,
0
1
2000
06
,
1
75
,
0
1
06
,
1
75
,
0
1
06
,
1
75
,
0
50000
06
,
1
25
,
0
17
8
17
8
52080
52084
≈
≈
Zadanie 4
Dla i-tego scenariusza
[
]
0
;
03
,
0
)
1
,
0
(
max
8
,
0
1000
1
−
⋅
=
i
i
R
PS
[
]
0
;
03
,
0
)
2
,
1
(
max
8
,
0
1200
2
−
⋅
=
i
i
R
PS
073
,
0
4
,
0
1
,
0
3
,
0
06
,
0
3
,
0
05
,
0
)
1
,
0
(
1
=
⋅
+
⋅
+
⋅
=
R
081
,
0
12
,
0
4
,
0
)
04
,
0
07
,
0
(
3
,
0
)
2
,
1
(
1
=
⋅
+
+
=
R
111
,
0
015
,
0
4
,
0
)
23
,
0
12
,
0
(
3
,
0
)
1
,
0
(
2
=
⋅
+
+
=
R
089
,
0
02
,
0
4
,
0
)
17
,
0
1
,
0
(
3
,
0
)
2
,
1
(
2
=
⋅
+
+
=
R
133
,
0
1
,
0
4
,
0
)
18
,
0
13
,
0
(
3
,
0
)
1
,
0
(
3
=
⋅
+
+
=
R
074
,
0
02
,
0
4
,
0
)
14
,
0
08
,
0
(
3
,
0
)
2
,
1
(
3
=
⋅
+
+
=
R
053
,
0
02
,
0
4
,
0
)
12
,
0
03
,
0
(
3
,
0
)
1
,
0
(
4
=
⋅
+
+
=
R
047
,
0
05
,
0
4
,
0
)
08
,
0
01
,
0
(
3
,
0
)
2
,
1
(
4
=
⋅
+
+
=
R
4
,
34
043
,
0
800
1
1
=
⋅
=
PS
96
,
48
051
,
0
960
1
2
=
⋅
=
PS
8
,
64
081
,
0
800
2
1
=
⋅
=
PS
64
,
56
059
,
0
960
2
2
=
⋅
=
PS
4
,
82
103
,
0
800
3
1
=
⋅
=
PS
24
,
42
044
,
0
960
3
2
=
⋅
=
PS
4
,
18
023
,
0
800
4
1
=
⋅
=
PS
32
,
16
017
,
0
960
4
2
=
⋅
=
PS
å
=
≈
÷÷
ø
ö
çç
è
æ
+
+
+
+
+
+
+
=
+
=
4
1
2
2
2
1
84
,
84
05
,
1
32
,
16
24
,
42
64
,
56
96
,
48
05
,
1
4
,
18
4
,
82
8
,
64
4
,
34
25
,
0
05
,
1
05
,
1
25
,
0
i
i
i
PS
PS
ODP
Zadanie 5
Dygresje:
v
nv
a
I
nv
v
v
v
v
I
nv
v
v
Iv
nv
v
v
I
n
n
n
n
n
n
−
−
=
→
−
+
+
+
=
−
+
+
+
=
+
+
+
=
+
+
+
1
...
)
1
(
...
2
...
2
1
1
2
1
3
2
2
v
v
v
a
I
v
v
v
v
v
I
v
v
v
Iv
v
v
v
I
−
−
+
=
→
−
+
+
+
=
−
+
+
+
=
+
+
+
=
1
30
15
30
...
16
)
1
(
30
...
17
16
30
...
17
16
16
15
16
15
2
16
3
2
15
2
20
20
20
21
20
08
,
0
20
1
20
08
,
0
v
a
v
v
v
a
DA
+
+
−
−
=
15
15
15
16
15
15
16
15
2
1
30
15
2
1
15
a
v
a
v
v
v
a
v
v
v
a
DP
+
−
−
+
+
−
−
=
5
,
2
≈
−
DA
DP
Zadanie 6
Butterfly oznacza,
ż
e:
Kupujemy 1 opcj
ę
po cenie
1
X
Wystawiamy 2 opcje po cenie
2
X
Kupujemy 1 opcj
ę
po cenie
3
X
3
2
1
X
X
X
<
<

profil wypłaty:
dla
0
1
X
S
<
dla
[
)
1
2
1
;
X
S
X
X
S
−
∈
dla
[
)
(
)
S
X
X
X
S
X
S
X
X
S
−
−
=
−
−
−
∈
1
2
2
1
3
2
2
2
2
;
dla
[
)
(
)
1
2
2
2
;
3
2
3
2
1
3
−
−
=
−
+
−
−
−
∞
∈
X
X
X
S
X
S
X
S
X
S
z powy
ż
szego i z obrazka wynika:
dla
2
X
S
=
zaczyna male
ć
czyli
120
2
=
X
-
opcja 2
dla
1
X
S
=
zaczyna rosn
ąć
czyli
100
1
=
X
-
opcja 1
oraz
150
10
100
120
2
10
2
3
3
1
3
2
=
→
−
=
−
−
⋅
→
−
=
−
−
X
X
X
X
X
-
opcja 3
P(i) – cena opcji nr i
gdzie
Xe
S
P
P
RT
C
P
,
−
+
−
=
P
P
- cena opcji sprzeda
ż
y
C
P
- cena opcji kupna
S – cena instrumentu bazowego
X – cena wykonania
R – stopa wolna od ryzyka
05
,
0
05
,
0
100
3
,
121
)
1
(
100
120
)
1
(
3
,
1
−
−
−
=
→
+
−
=
e
P
e
P
05
,
0
05
,
0
120
7
,
126
)
2
(
120
120
)
2
(
7
,
6
−
−
−
=
→
+
−
=
e
P
e
P
05
,
0
05
,
0
150
5
,
145
)
3
(
150
120
)
3
(
5
,
25
−
−
−
=
→
+
−
=
e
P
e
P
9
,
3
4
,
13
10
)
3
(
)
2
(
2
)
1
(
05
,
0
≈
+
−
=
+
−
=
−
e
P
P
P
ODP
Zadanie 7
DL(8) – dług po spłacie 8 raty
DL(7) – dług po spłacie 7 raty
Kapitał spłacony w 8 racie = DL(7)-DL(8)
ODP=18-DL(7)+DL(8)
18 – 8 rata
8
2
25
...
19
18
)
7
(
v
v
v
DL
+
+
+
=
7
2
25
...
20
19
)
8
(
v
v
v
DL
+
+
+
=
(
)
=
−
−
−
−
+
+
+
−
=
7
2
8
2
25
...
20
19
25
...
19
18
18
v
v
v
v
v
v
ODP
(
)
8
8
8
7
8
7
2
25
17
25
18
25
...
18
v
a
v
a
v
v
v
v
−
+
=
−
+
=
+
−
−
−
−
−
=
&
&
Zadanie 8
n
n
n
v
n
v
v
v
v
v
dura
1
...
2
1
...
2
2
+
+
+
+
+
+
=
n
n
n
nv
v
v
v
n
v
v
durb
+
+
+
+
+
+
=
...
2
...
2
2
2
2
2
n
n
n
a
v
a
dura
&
&
=
≤
n
n
n
a
n
v
a
n
durb
&
&
2
2
=
≤
st
ą
d
( )
n
n
a
n
D
&
&
2
1
+
≤
1
=
≥
n
n
n
a
a
dura
v
nv
a
Ia
a
nv
a
v
Ia
a
durb
n
n
n
n
n
n
n
n
n
−
−
=
−
−
=
≥
+
+
1
bo
1
1
1
( )
n
n
n
n
n
n
n
a
v
durb
v
v
v
v
v
i
a
nv
a
2
1
)
1
(
1
1
1
1
1
1
1
−
≥
→
−
≥
−
−
=
−
=
≥
−
+
czyli:
(
)
n
n
n
a
n
D
a
v
&
&
2
2
1
)
1
(
1
+
≤
≤
−
+
Zadanie 9
1
p
- prawdopodobie
ń
stwo hossy
2
p
- prawdopodobie
ń
stwo bessy
wtedy:
r
p
p
+
+
1
4
2
1
4
,
1
1
2
2
1
=
+
+
r
p
p
î
í
ì
+
=
+
+
=
+
)
1
(
4
,
1
2
)
1
(
1
,
2
4
2
1
2
1
r
p
p
r
p
p
Z tego:
)
1
(
4
,
0
1
r
p
+
=
)
1
(
5
,
0
)
1
(
6
,
1
)
1
(
1
,
2
2
r
r
r
p
+
=
+
−
+
=
9
1
1
)
1
(
9
,
0
1
2
1
=
→
=
+
→
=
+
r
r
p
p
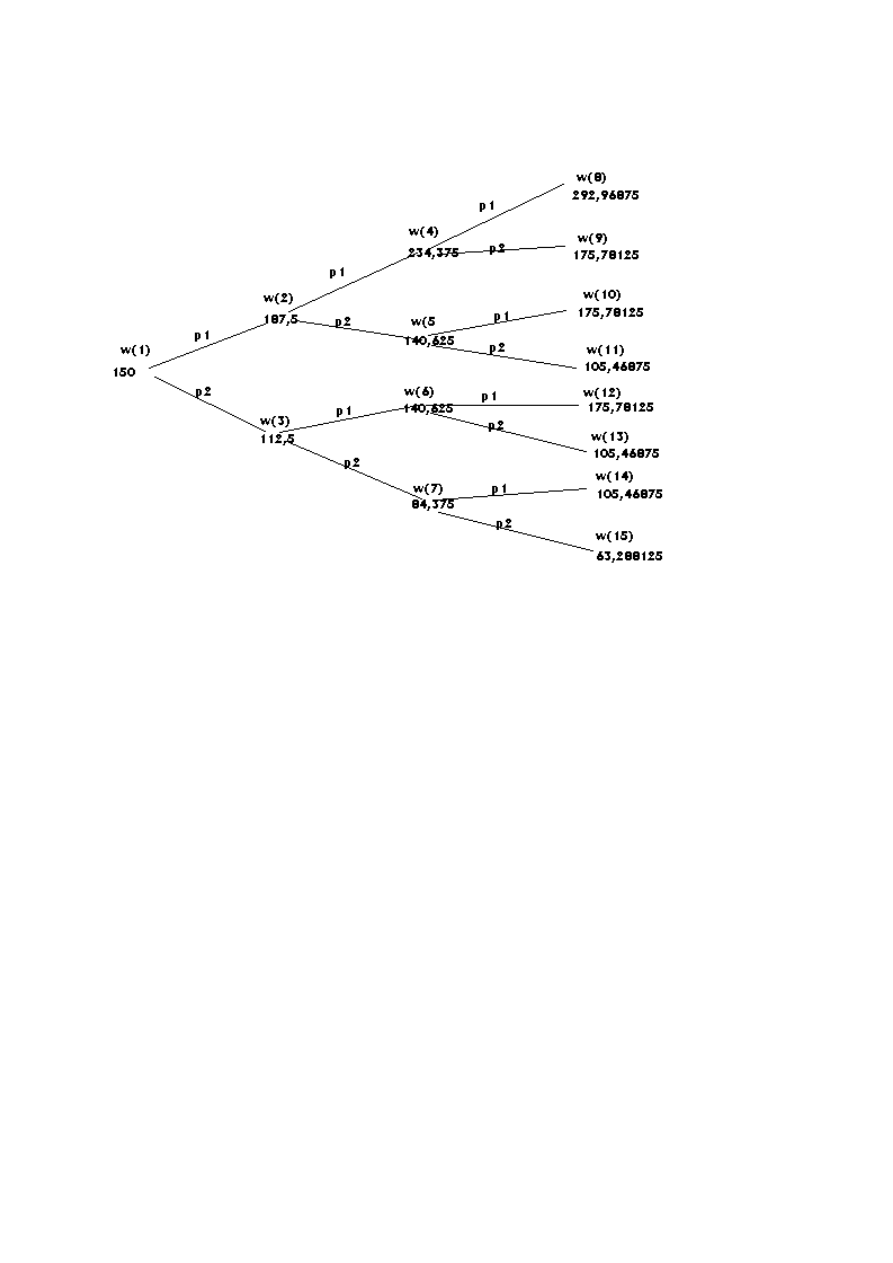
Zadanie 10
w(i) – numery w
ę
złów
c(i) – cena opcji w w
ęź
le i
z braku arbitra
ż
u mamy:
ïî
ï
í
ì
−
=
−
=
→
î
í
ì
=
+
=
+
07
,
0
2
07
,
0
1
2
1
07
,
0
2
1
2
5
,
2
5
,
1
2
1
150
5
,
112
5
,
187
e
p
e
p
p
p
e
p
p
wyceniamy od prawej strony:
c(8)=c(9)=c(10)=0
c(11)=160-105,46875=54,53125
c(12)=0
c(13)=54,53125
c(14)=54,53125
c(15)=96,711875
c(4)=0
07
,
0
2
)
11
(
)
5
(
−
⋅
=
e
c
p
c
07
,
0
2
)
13
(
)
6
(
−
=
e
c
p
c
[
]
07
,
0
2
1
)
15
(
)
14
(
)
7
(
−
+
=
e
c
p
c
p
c
07
,
0
2
)
5
(
)
2
(
−
=
e
p
c
c
[
]
07
,
0
2
1
)
7
(
)
5
(
)
3
(
−
+
=
e
c
p
c
p
c
[
]
[
]
=
+
+
=
+
=
=
⋅
−
−
2
07
,
0
2
2
2
1
2
1
07
,
0
2
1
)
7
(
)
5
(
)
5
(
)
3
(
)
2
(
)
1
(
e
c
p
c
p
p
c
p
p
e
c
p
c
p
c
ODP
[
]
=
+
+
+
=
⋅
−
−
−
−
−
2
07
,
0
07
,
0
2
2
2
07
,
0
1
2
2
07
,
0
2
2
1
07
,
0
2
2
1
)
15
(
)
14
(
)
11
(
)
11
(
e
e
c
p
p
e
c
p
p
e
c
p
p
p
e
c
p
p
p
[
]
20
)
15
(
)
14
(
)
11
(
2
07
,
0
3
3
2
2
2
1
2
2
1
≈
+
+
=
⋅
−
e
c
p
c
p
p
c
p
p
Wyszukiwarka
Podobne podstrony:
2008.10.06 matematyka finansowa
mat fiz 2008 10 06
2008 10 06 praid 26459 Nieznany
2004 10 11 matematyka finansowaid 25165
1 2006 10 09 matematyka finansowaid 8919
2003.12.06 matematyka finansowa
mat fiz 2008.10.06
1 2009 10 05 matematyka finansowaid 8924
2008 03 17 matematyka finansowaid 26447
2002 10 12 matematyka finansowaid 21647
2007.10.08 matematyka finansowa
2008.10.06 prawdopodobie stwo i statystyka
1 2009.04.06 matematyka finansowa
1 2009.10.05 matematyka finansowa
2008.12.15 matematyka finansowa
2004.10.11 matematyka finansowa
2008.03.17 matematyka finansowa
2008 12 15 matematyka finansowaid 26464
1 2006.10.09 matematyka finansowa
więcej podobnych podstron