Zadanie 20

Twierdzenia o działaniach na logarytmach (Uwaga we wszystkich tw. zakładamy, że liczby logarytmowane są dodatnie, a podstawy logarytmów są dodatnie i różne od 1 )

1. logarytm iloczynu równa się sumie logarytmów:

Założenia:

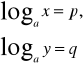
Teza:

Dowód:

z określenia logarytmu wynika:

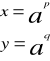
stąd:

więc:

QED

2. logarytm ilorazu równa się różnicy logarytmów:

Założenia:

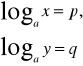
Teza:

Dowód:

z określenia logarytmu wynika:

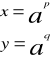
stąd:

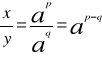
więc:

QED

3. Logarytm potęgi równa się iloczynowi wykładnika przez logarytm podstawy:

Założenia:

x > 0

Teza:

Dowód:

z określenia logarytmu wynika:

więc:

czyli:

QED

4. Wzór na zamianę podstaw:

Założenia:

x > 0

Teza:

Dowód:

z określenia logarytmu:

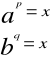
więc:

równe liczby dodatnie mają równe logarytmy:

czyli:

stąd:

QED