35. Ciąg arytmetyczny, geometryczny, definicje, wzory, własności.

Ciągiem arytmetycznym nazywamy taki ciąg liczbowy, w którym różnica między kolejnymi wyrazami jest stała (każdy wyraz z wyjątkiem pierwszego powstaje przez dodanie do poprzedniego wyrazu stałej liczby (r) ).

Aby zdefiniować ciąg arytmetyczny musimy mieś dany:

1. dowolne 2 wyrazy

2. dowolny wyraz i różnicę

(a_n - n-ty wyraz ciągu; a₁ - pierwszy wyraz; r - różnica ciągu arytmetycznego)

- wzór na dowolny wyraz ciągu

- różnica ciągu arytmetycznego

- suma częściowa ciągu arytmetycznego

wyprowadzenie

S_n = (a₁ + a₂ + a₃ + a₄ + … + a_n-3 + a_n-2 + a_n-1 a_n)

S_n = (a₁ + a_n) + (a₂ + a_n-1) + (a₃ + a_n-2) + (a₄ + a_n-3) + …

S_n = (a₁ + a_n) + (a₁ + a_n) + (a₁ + a_n) + …

W ciągu arytmetycznym każdy wyraz, oprócz skrajnych, jest średnią arytmetyczną swoich sąsiadów

Monotoniczność ciągu:

r > 0 ciąg rosnący

r < 0 ciąg malejący

r = 0 ciąg stały

Ciągiem geometrycznym nazywamy taki ciąg liczbowy, w którym każdy wyraz, oprócz pierwszego, powstaje przez pomnożenie poprzedniego wyrazu przez stałą liczbę, zwaną ilorazem tego ciągu (q).

(a_n - n-ty wyraz ciągu; a₁ - pierwszy wyraz; q - iloraz ciągu geometrycznego)

- wzór na dowolny wyraz ciągu

W ciągu geometrycznym iloraz dwóch sąsiednich wyrazów jest stały

(z wyjątkiem ciągu stałego, gdzie wynosi 0)

lub

=>

Suma częściowa ciągu geometrycznego:

=>

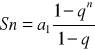
S_n = a₁ + a₂ + a₃ + a₄ + … + a_n-1 + a_n

S_nq = a₁q + a₂q + a₃q + a₄q + … + a_n-1q + a_nq

S_n = a₂ + a₃ + a₄ + a₅ + … + a_n + a_n+1

S_n - S_nq = a₁ - a_n+1

S_n(1 - q) = a₁ - a₁qⁿ

S_n(1 - q) = a₁(1 - qⁿ)

=>

Monotoniczność ciągu:

a₁ >0
q>0

a₁ <0
q
(0,1)

a₁ <0
q>0

a₁ >0
q
(0,1)

q<0 ciąg naprzemienny

q=1 ciąg stały

Szeregiem geometrycznym zbieżnym nazywamy nieskończony ciąg geometryczny, w którym spełniony jest warunek |q|<1 (tzw. warunek zbieżności)

- suma nieskończonego ciągu geometrycznego

ciąg rosnący

ciąg malejący

---