Funkcje trygonometryczne:
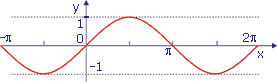
Funkcja y = sinx
Dziedzina: x∈R; y∈<-1,1>
Okres 2π
Miejsca zerowe x = kπ
Maksima (π/2 + 2kπ, 1)
Minima (-π/2 + 2kπ, -1)
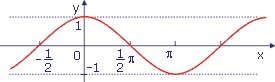
Funkcja y = cosx
Dziedzina: x∈R; y∈<-1,1>
Okres 2π
Miejsca zerowe x = π/2 + kπ
Maksima (2kπ, 1)
Minima ((2k - 1)π, -1)
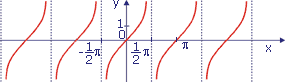
Funkcja y = tgx
Dziedzina: x∈R - {π/2 + kπ}; y∈R
Okres π
Miejsca zerowe x = kπ
Asymptoty pionowe x = π/2 + kπ
Funkcja rośnie przedziałami w całej dziedzinie
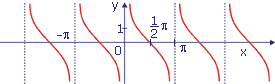
Funkcja y = ctgx
Dziedzina: x∈R - {kπ}; y∈R
Okres π
Miejsca zerowe x = π/2 + kπ
Asymptoty pionowe x = kπ
Funkcja maleje przedziałami w całej dziedzinie
k∈C
WZORY REDUKCYJNE:
sin (360o + α) = sin α
cos (360o + α) = cos α
tg (360o + α) = tg α
ctg (360o + α) = ctg α
sin (180o - α) = sin α
cos (180o - α) = - cos α
tg (180o - α) = - tg α
ctg (180o - α) = - ctg α
sin (180o + α) = - sin α
cos (180o + α) = - cos α
tg (180o + α) = tg α
ctg (180o + α) = ctg α
sin (360o - α) = - sin α
cos (360o - α) = cos α
tg (360o - α) = - tg α
ctg (360o - α) = - ctg α
sin (90o - α) = cos α
cos (90o - α) = sin α
tg (90o - α) = ctg α
ctg (90o - α) = tg α
sin (90o + α) = cos α
cos (90o + α) = - sin α
tg (90o + α) = - ctg α
ctg (90o + α) = - tg α
sin (270o - α) = - cos α
cos (270o - α) = - sin α
tg (270o - α) = ctg α
ctg (270o - α) = tg α
sin (270o + α) = - cos α
cos (270o + α) = sin α
tg (270o + α) = - tg α
ctg (270o + α) = - ctg α
Wyszukiwarka
Podobne podstrony:
TM36, materialy, Matematyka, matematyka - dowody
tm29, materialy, Matematyka, matematyka - dowody
zadanie6, materialy, Matematyka, matematyka - dowody
tm16, materialy, Matematyka, matematyka - dowody
tm4-2, materialy, Matematyka, matematyka - dowody
tm3, materialy, Matematyka, matematyka - dowody
zadanie18, materialy, Matematyka, matematyka - dowody
tm35ciagi, materialy, Matematyka, matematyka - dowody
Iloczynkartezjaski, materialy, Matematyka, matematyka - dowody
tm5, materialy, Matematyka, matematyka - dowody
PROSTA, materialy, Matematyka, matematyka - dowody
tm4, materialy, Matematyka, matematyka - dowody
tm2Twierdzeniecosinusw, materialy, Matematyka, matematyka - dowody
TM31Wartbezwzgl, materialy, Matematyka, matematyka - dowody
kombinatorykaTM41, materialy, Matematyka, matematyka - dowody
ZadanieTM20, materialy, Matematyka, matematyka - dowody
ZBIORY, materialy, Matematyka, matematyka - dowody
TRYGONOMETRIA1, materialy, Matematyka, matematyka - dowody
więcej podobnych podstron