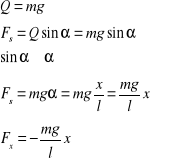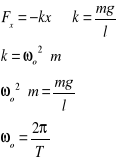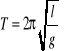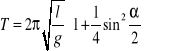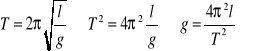Ćwiczenie nr 7

WYZNACZANIE WARTOŚCI PRZYŚPIESZENIA

ZIEMSKIEGO

1. Cel ćwiczenia

Wyznaczenie wartości przyśpieszenia ziemskiego przy pomocy wahadła matematycznego

2. Wprowadzenie

Wahadłem matematycznym nazywamy ciało o masie m i o małej objętości zawieszone na nieważkiej i nierozciągliwej nici. Warunek ten spełnia między innymi kulka zawieszona na nici, gdy rozmiary liniowe kulki są dużo mniejsze od długości nici. W położeniu równowagi ciężar ciała Q=mg jest zrównoważony siłą sprężystości nici.

Jeżeli odchylimy kulkę od położenia równowagi o niewielki kąt α i puścimy swobodnie będzie się ona poruszała ruchem harmonicznym prostym.Za ruch wahadła odpowiada wypadkowa siła F_s będąca składową siły ciężkości Q:

Rys. 7.1 Rozkład sił działających na wahadło matematyczne

	(7.1)
		(7.2)
		(7.3)
		(7.4)
		(7.5)

W ruchu harmonicznym prostym siła działająca na drgające ciało F jest wprost proporcjonalna do wychylenia z położenia równowagi x i zwrócona w stronę położenia równowagi:

(7.6)

gdzie k oznacza stałą proporcjonalności.

Warunek ten spełnia siła F_x:

	(7.7)
		(7.8)
		(7.9)
		(7.10)

gdzie:

m - masa drgającego obiektu.

T - okres drgań,

l - długość wahadła,

ω_o - częstość kołowa drgań własnych,

g - wartość przyspieszenia ziemskiego.

Po przekształceniach otrzymujemy wzór na okres T wahadła matematycznego:

(7.11)

Wzór na okres wahadła matematycznego został wyprowadzony przy założeniu, że wahadło zostało odchylone od położenia równowagi o mały kąt α≤ 5^o a wartość kąta wychylenia była podawana w radianach. Okres T zależy tylko od długości wahadła l i wartości przyspieszenia g. Niezależność okresu drgań od wartości wychylenia nazywamy izochronizmem drgań.

Dla większych wychyleń należy uwzględnić wartość kąta wychylenia od położenia równowagi α:

(7.12)

Wahadło matematyczne pozwala na doświadczalne wyznaczenie wartości przyspieszenia ziemskiego g. Newton podał prawo powszechnej grawitacji obowiązujące w całym wszechświecie.

Każde dwa ciała przyciągają się wzajemnie siłami grawitacji. Każde dwa punkty materialne przyciągają się wzajemnie z siłą proporcjonalną do iloczynu ich mas, a odwrotnie proporcjonalna do kwadraty odległości pomiędzy nimi.

(7.13)

gdzie:

m₁, m₂- masy ciał

r - odległość pomiędzy nimi

G - stała grawitacji, G=6,6*10^-11 Nm²/kg^-2

Siły wzajemnego przyciągania leżą na prostej łączącej oba punkty materialne

Siła, z jaką ciało o masie m jest przyciągane przez Ziemię (siła ciężkości-ciężar) jest równa:

(7.14)

gdzie:

m - masa ciała,

g - przyśpieszenie uzyskiwane pod wpływem siły ciężkości(przyspieszenie ziemskie).

Wartość przyśpieszenia ziemskiego g nie jest jednakowa we wszystkich miejscach na kuli ziemskiej. Wynika to z faktu, że Ziemia jest faktycznie elipsoidą obrotową nieco spłaszczoną przy biegunach, ruchu dobowego Ziemi oraz z niejednorodności budowy skorupy ziemskiej. Uwzględnienie ruchu obrotowego prowadzi do pojęcia ciężaru pozornego, a wartość przyśpieszenia ziemskiego zależy od szerokości geograficznej według wzoru Helmerta:

(7.15)

g_o = 9,78 m/s²- wartość g na równiku.

3. Opis stanowiska laboratoryjnego

Wahadło matematyczne, statyw do zawieszania wahadła, przymiar liniowy, stoper.

4. Program ćwiczenia

1. Zawiesić kulkę ze sznurkiem na haczyku tak, aby uzyskać maksymalną długość wahadła.

2. Odchylić kulkę o kąt około 5^o od położenia równowagi i puścić swobodnie. Prawidłowo ruch wahadła powinien się odbywać w jednej płaszczyźnie.

3. Zmierzyć przy pomocy stopera czas t_n dla n=20 okresów wahadła i następnie obliczyć okres T= t_n/n.

4. Zmierzyć długość wahadła od punktu zawieszenia do środka kulki.

5. Określić niepewności pomiarowe długości wahadła Δl, pomiaru czasu Δt₁,okresu ΔT.

6. Zmieniać długość wahadła od długości maksymalnej do około 30 cm co 10 cm i powtarzać czynności z punktów 2-5.

7. Wyniki pomiarów umieścić w tabeli 7.1.

Tabela 7.1

Lp.	l[m]	Δl[m]	tn [s]	Δtn [s]	T [s]	ΔT [s]	T^2[s^2]	ΔT^2[s^2]

ΔT² wyliczone metodą różniczki zupełnej wynosi: ΔT²=2T ΔT.

5. Sprawozdanie

Do obliczeń wykorzystujemy wzór na okres wahadła matematycznego i po przekształceniach otrzymujemy zależność przyśpieszenia ziemskiego od mierzonych wielkości:

(7.16)

1. Korzystając z programu „regresja liniowa „ lub korzystając z arkusza kalkulacyjnego Excel sprawdzić liniowość wykresu T²=f(l). oraz zapisać wyliczone przez program współczynniki regresji a, b równania prostej y=ax+b oraz ich odchylenia standardowe i współczynnik korelacji. Na podstawie otrzymanej wartości współczynnika kierunkowego prostej a obliczyć wartość g. i zapisać ją wraz z jednostką.

2. Wykonać wykres zależności T² od długości wahadła T²=f(l). Nanieść niepewności systematyczne. Sprawdzić czy punkty pomiarowe układają się wzdłuż prostej.

3. Narysować prostą przechodzącą przez największa ilość prostokątów niepewności pomiarowych. Wyznaczyć współczynnik nachylenia prostej na tej podstawie wyznaczyć wartość g i zapisać ją wraz z jednostką

4. Korzystając z danych z tabeli 7.1 wyliczyć wartość g dla wszystkich długości wahadła. Obliczyć również względną niepewność systematyczną przyśpieszenia ziemskiego ze wzoru:

(7.17)

5. Wyniki obliczeń przedstawić w tabeli 7.2.

Tabela 7.2

lp.	l[m]	T [s]	g[m/s^2]	Δl/l	2ΔT/T	Δg/g	Δg/g [%]	Δg [m/s^2]

Uwaga: wartość niepewności bezwzględnej Δg otrzymujemy mnożąc wyliczoną maksymalną niepewność względną pomiaru Δg/g przez otrzymaną doświadczalnie wartość przyspieszenia g. Czynność tą powtarzamy dla wszystkich długości wahadła

6. Przeprowadzić dyskusje wyników i niepewności pomiarowych.

6. Pytania kontrolne

1. Pole grawitacyjne i wielkości definiujące to pole.

2. Ciężar ciała.

3. Zależność pomiędzy przyśpieszeniem ziemskim a natężeniem pola grawitacyjnego.

4. Praca w polu grawitacyjnym.

5. Prawa Kuplera.

6. Czynniki wpływające na wartość g.

7. Ruch harmoniczny prosty.

49

0

x

F_s

Q =m g

N

α

---