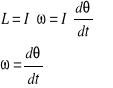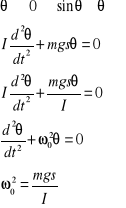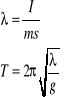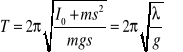Ćwiczenie nr 8

WYZNACZANIE PRZYŚPIESZENIA ZIEMSKIEGO g ZA POMOCĄ WAHADŁA REWERSYJNEGO

1. Cel ćwiczenia

Wyznaczenie zredukowanej wahadła rewersyjnego, wyznaczenie wartości przyspieszenia ziemskiego g

2. Wprowadzenie

Wahadłem fizycznym nazywamy bryłę sztywną zawieszoną w punkcie A nieprzechodzącym przez środek masy. Jeżeli wahadło odchylimy od położenia równowagi o kąt θ i puścimy swobodnie to pod wpływem siły ciężkości będzie wykonywało drgania harmoniczne. Wtedy na wahadło działa moment siły M:

(8.1)

gdzie:

s - odległość pomiędzy osią obrotu a środkiem masy,

m - masa bryły.

Zgodnie z II zasadą dynamiki dla ruchu obrotowego moment sił zewnętrznych jest równy zmianie w czasie momentu pędu L:

(8.2)

Moment pędu L można zapisać wzorem:

	(8.3)
		(8.4)

gdzie:

I - moment bezwładności bryły sztywnej,

ω - prędkość kątowa ruchu obrotowego.

Moment siły ciężkości zapiszemy w postaci:

(8.5)

Podstawiając powyższe równanie do równania 8.1 otrzymujemy równanie różniczkowe ruchu wahadła fizycznego:

(8.6)

dla małych kątów θ dostajemy równanie:

	(8.7)
		(8.8)
		(8.9)
		(8.10)
		(8.11)

Jest to równanie ruchu harmonicznego , o ile częstotliwość drgań kątowych ω₀ wynosi:

(8.12)

którego rozwiązaniem jest funkcja okresowa:

(8.13)

gdzie
jest amplitudą kątową drgań, φ_o fazą początkowa drgań.

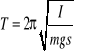
Okres drgań wahadła fizycznego można zapisać wzorem:

(8.14)

Wprowadzając definicję długości zredukowanej λ okres drgań wahadła fizycznego okres drgań T można zapisać analogicznie jak dla wahadła matematycznego:

	(8.15)
		(8.16)

W ćwiczeniu posługujemy się wahadłem rewersyjnym (odwracalnym) pokazanym na rysunku 8.1.

Rys. 8.1. Wahadło rewersyjne

Źródło: Phywe

Stanowi je stalowy pręt wraz z umocowanymi dwoma pierścieniami. Pierścienie można przemieszczać wzdłuż pręta i posiadają one nacięcia, na których można je zawiesić na ostrzach służących jako osie obrotu. Oś obrotu jest zamocowana w statywie. Moment bezwładności takiego wahadła zawieszonego na jednym z pierścieni można wyznaczyć z twierdzenia Steinera:

(8.17)

gdzie:

I_o - moment bezwładności wahadła względem osi przechodzącej przez środek masy

s -odległość środka masy od punktu zawieszenia A.

Dla wahadła rewersyjnego okres drgań zapiszemy wzorem:

(8.17)

gdzie długość zredukowaną λ zapiszemy wzorem:

(8.18)

Jeżeli ze wzoru na okres T wyznaczymy odległość punktu zawieszenia od środka masy s otrzymamy z równania kwadratowego dwa różne pierwiastki s₁ i s₂ .Ze wzoru na sumę pierwiastków równania kwadratowego otrzymamy:

(8.19)

Suma obu odległości od osi obrotu jest równa długości zredukowanej wahadła fizycznego.

Dla danej wartości l równej odległości pomiędzy dwoma pierścieniami mamy dwie odległości s, dla których okres wahadła będzie taki sam. Stanowi to podstawę wyznaczenia długości zredukowanej wahadła, a następnie wyliczenia wartości przyspieszenia ziemskiego za pomocą wahadła rewersyjnego. W tym celu zawieszamy wahadło na jednym z pierścieni, mierzymy odległość pomiędzy nimi i wyznaczamy okres drgań T₁.Nastepnie odwracamy wahadło i zawieszamy je na drugim pierścieniu, aby zmierzyć okres T₂ przy tej samej odległości l. Zmieniając odległości pomiędzy pierścieniami dokonujemy ponownych pomiarów. Graficzną metodę wyznaczenia długości zredukowanej wahadła pokazano na rysunku 2. Po wyznaczeniu długości zredukowanej λ można obliczyć wartość przyspieszenia ziemskiego g.

Rys. 8.2 Graficzna metoda wyznaczenia zredukowanej długości wahadła.

Źródło: Phywe

3. Opis stanowiska laboratoryjnego

Zestaw pomiarowy składa się z wahadła rewersyjnego posiadającego przesuwalne pierścienie wraz z nacięciami służącymi do zawieszania wahadła, statywu wraz o osiami do zawieszania wahadła, przymiaru liniowego, bramki świetlnej.

Rys. 8.3 Wahadło rewersyjne z bramką świetlną

Źródło: Phywe

4. Program ćwiczenia:

1. Zapoznać się z zasadą działania bramki świetlnej. Przełącznik rodzaju pracy ustawić tak, aby mierzył czas jednego okresu drgań

2. Przykręcić jeden z pierścieni w odległości około 8 cm od góry pręta. Ten pierścień nie zmienia swojego położenia do końca ćwiczenia. Drugi z pierścieni zamocować na drugim końcu pręta.

3. Zawiesić górny pierścień na osi obrotu.

4. Zmierzyć odległość pomiędzy pierścieniami l.

5. Zmierzyć za pomocą bramki okres drgań T₁.

6. Odwrócić wahadło rewersyjne i ponownie zawiesić na drugim pierścieniu

7. Zmierzyć za pomocą bramki okres drgań T₂.

8. Ustalić i zapisać niepewności pomiarowe Δl, ΔT_1, ΔT₂.

9. Ponownie zawiesić wahadło na górnym pierścieniu umocowanym na stałe

10. Dolny pierścień przesunąć o około 2 cm w kierunku górnego pierścienia. Ponownie powtórzyć czynności z punktu 5-9.

11. Wyniki pomiarów zapisać w tabeli 8.1.

Tabela 8.1

Δl = ΔT₁= ΔT₂=

lp.	l [m]	T1 [s]	T2 [s]
1 2 . . n

5. Sprawozdanie

1. Sporządzić wykres zależności T₁ od odległości pomiędzy pierścieniami l oraz na tym samym rysunku przedstawić zależność T₂ od l.

2. Z wykresu odczytać współrzędne punktu przecięcia się dwóch krzywych i zanotować zredukowaną długość wahadła.

3. Obliczyć wartość przyśpieszenia ziemskiego g ze wzoru:

(8.20)

4. Obliczyć względną niepewność pomiarową g korzystając ze wzoru:

(8.21)

5. Zapisać otrzymaną doświadczalnie wartość g wraz z niepewnością bezwzględną Δg. Wartość Δg otrzymamy mnożąc obliczoną wartość Δg/g przez otrzymaną wartość g.

6. Przeprowadzić dyskusje wyników i niepewności pomiarowych.

6. Pytania kontrolne

1. Ruch harmoniczny prosty.

2. Wahadło matematyczne i fizyczne.

3. Bryła sztywna, momenty bezwładności, twierdzenie Steinera

4. Definicja momentu pędu i momentu siły.

5. Zasady dynamiki dla bryły sztywnej.

6. Prawo powszechnego ciążenia, przyspieszenie ziemskie,

57

---