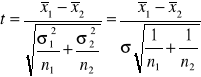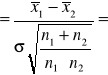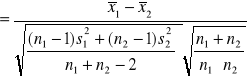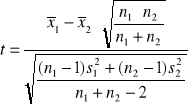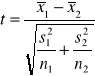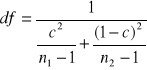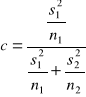Postać ogólna testu t-Studenta dla dwóch prób niezależnych

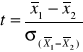
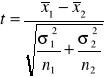
Oszacowanie σ² zależy od tego czy próby są homogeniczne czy heterogeniczne

Weryfikacja homogeniczności prób równość wariancji

Test Fishera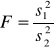

Jeżeli F < Fα; df1, df2 H0+ Wariancje homogeniczne	Jeżeli F > Fα; df1, df2 H0- Wariancje heterogeniczne
Mamy jedną i tę samą σ^2 - do jej szacowania można użyć estymatora łącznego wariancji.	Dwie różne σ^2 , szacujemy je oddzielnie dla obu prób na podstawie s^2.
Test t-Studenta przekształcamy: - wyciągamy σ przed pierwiastek: = - sprowadzamy ułamki pod pierwiastkiem do wspólnego mianownika - a za σ podstawiamy estymator łączny - żeby uprościć zapis - przerzucamy jeden moduł do licznika - w ostatecznej wersji otrzymujemy Stopnie swobody dla tej postaci testu to n1+n2-2	Test t-Studenta przyjmuje postać Jest to test Cox-Cochrana Stopnie swobody „GUBIMY” stopnie swobody na gorsze oszacowanie σ^2. Stopnie swobody dla testu Cox-Cochrana to: Gdzie

Test t-Studenta dla jednej próby

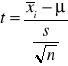
Stopnie swobody n-1

Test t-Studenta dla dwóch prób zależnych

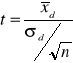
Oszacowanie σ - na podstawie wartości odchylenia standardowego różnicy wyników:

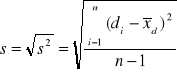
Stopnie swobody n-1

Test t-Studenta - podsumowanie

Test t-Studenta ma ZAWSZE postać standaryzacji danego estymatora przy założeniu prawdziwości hipotezy zerowej (która zawsze ma postać prostą! Równościową!)

ZAWSZE w mianowniku jest błąd standardowy (odchylenie standardowe w określonym rozkładzie z próby)

Dla 1 próby

Standaryzacja średniej w próbie przy założeniu, że µ jest równe testowanej wartości, µ = c.

Dla 2 prób niezależnych

Standaryzacja różnicy średnich w dwóch próbach, przy założeniu, że µ₁ - µ₂ = 0.

Dla 2 prób zależnych

Standaryzacja średniej różnic, przy założeniu, że µ₁ - µ₂ = 0.