1. Rachunek zdań

Będziemy posługiwać się językiem, który składa się ze zdań. Interesuje nas budowa logiczna zdań, tzn. że zdaniom przyporządkowujemy wartości logiczne: prawda lub fałsz.

Funkcją zdaniową nazywamy wyrażenie, które zawiera zmienną przyjmującą wartości z pewnego niepustego zakresu, przy czym po podstawieniu zamiast zmiennej konkretnej wartości otrzymujemy zawsze zdanie prawdziwe lub fałszywe.

f(p) dla p
X ( p należy do X)

jest funkcją zdaniową jednej zmiennej

Wyrażenie

f(p₁…p _n) dla p_i
X_i i=1,2….n

jest funkcją zdaniową n-zmiennych.

Zmienna w funkcji zdaniowej może przyjmować wartości, które są zdaniami, wtedy mówimy o zmiennej zdaniowej.

Jeżeli p,q są zdaniami to przy pomocy tzw. funktorów zdaniotwórczych

♦ koniunkcja
(„oraz”)

♦ implikacja
(„implikuje”)

♦ alternatywa
(„lub”)

♦ równoważność
(„wtedy i tylko wtedy”)

można tworzyć zdania złożone. Natomiast jeżeli p,q są zmiennymi zdaniowymi to przy pomocy funktorów zdaniotwórczych można tworzyć funkcji zdaniowe.

♦ koniunkcję p
q

♦ implikację p
q

♦ alternatywę p
q

♦ równoważność p
q

Wartości logiczne funkcji zdaniowych

♦ koniunkcję p
q

♦ implikację p
q

♦ alternatywę p
q

♦ równoważność p
q

(p
q)
[( p
q)
( q
p)

Potwierdzenie zdania p to zdanie p.

Negacja zdania p to zdanie „nie p”.

Negację zdania p będziemy ozn. przez p'

Mówimy, że zdanie p jest warunkiem koniecznym dla zdania q, jeżeli jest prawdziwe zdanie q
p

Mówimy, że zdanie p jest warunkiem dostatecznym dla zdania q jeżeli jest prawdziwe zdanie p
q

Mówimy, że zdanie p jest warunkiem koniecznym i dostatecznym dla zdania q jeżeli jest prawdziwe zdanie p
q

Zmierzanie do zera wyrazów ciągu (a_n) jest warunkiem koniecznym, ale nie jest warunkiem dostatecznym, na to, by suma
a_k była liczbą skończoną

Funkcja zdaniowa, która po podstawieniu w miejsce zmiennych, zdań o dowolnej wartości logicznej jest zawsze zdaniem prawdziwym nazywamy tautologią.

Przykłady tautologii:

1. Prawo transpozycji

(q'
p')
(p
q)

2. Prawo sylogizmu

[(p
q)
(q
r)]
(p
r)

3. Prawa de Morgana

(p
q) '
(p'
q')

(p
q)'
(p'
q')

4. (p
   q)'
   (p
   q')

Sprawdzenie, czy funkcja zdaniowa jest tautologiczna dokonujemy tzw. metodą prób zerojedynkowych, która polega na zbadaniu wszystkich możliwych przypadków wartości logicznych zdań podstawianych w miejsce zmiennych.

2. Rachunek kwantyfikowany

Niech p(x) będzie funkcją zdaniową zmiennej x z pewnego niepustego zakresu X.

Kwantyfikatorem szczegółowym nazywamy słowo „istnieje” ozn.

Kwantyfikatorem ogólnym nazywamy słowo „dla każdego” ozn.

Wyrażenia
p(x) oraz
p(x) są zdaniami.

Zdanie, w którym kilka kwantyfikatorów poprzedza funkcję zdaniową, negujemy zamieniając kwantyfikatory szczegółowe na ogólne, a ogólne na szczegółowe i negując funkcję zdaniową. Na ogół nie zmieniamy miejsc kwantyfikatorów.

Kolejność kwantyfikatorów można zmieniać w następujących przypadkach:

Równoważność przy zmianie kwantyfikatora ogólnego i szczegółowego nie jest prawdziwa.

Jest słuszna implikacja.

Niech będzie dana funkcja zdaniowa p(x) dla x
X , w pewnych przypadkach budując

z p(x) zdanie, zawężamy zakres zmienności x, tzn. jeżeli bierzemy pod uwagę tylko te x
X dla których jest prawdą q(x)

wtedy

Kwantyfikatory

to tzw. kwantyfikatory o ograniczonym zakresie.

Przykład

Zdanie: nieprawda jest, że ciąg (a_n), gdzie a_n
, dla n=1,2,3…..ma granicę g
zapisujemy następująco

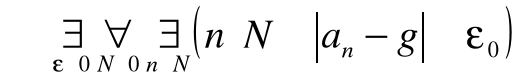
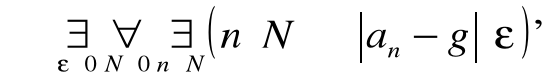
(p=>q)'(p
q')

5

---