WYPUKŁOŚĆ ORAZ WKLĘSŁOŚĆ FUNKCJI

Twierdzenie 4

Niech funkcja
będzie określona na
oraz posiada skończoną pochodną
na
.

Na to by funkcja
była wypukła
lub wklęsła
na
potrzeba i wystarcza, by

Definicja: Mówimy, że punkt
jest punktem przegięcia krzywej
, która jest wykresem funkcji ciągłej
, jeżeli w punkcie
zmienia się charakter wypukłości funkcji
. Tzn. w
funkcja
z wypukłej staje się wklęsła i na odwrót.

Uwaga: Jeżeli w otoczeniu punktu
dla funkcji
, która posiada skończoną pochodną
, w tym otoczeniu
, zmienia się znak
to w
istnieje punkt przegięcia wykresu funkcji
.

Uwaga:Niech funkcja
będzie określona na niepustym podzbiorze

Obok punktów zbioru
, w którym funkcja
posiada maksimum lokalne lub minimum lokalne, mogą w dziedzinie
, istnieć punkty, w których funkcja
przyjmuje wartość najmniejszą lub wartość największą.

ASYMPTOTY Niech będzie dana krzywa
, określona i ciągła na
o wartościach rzeczywistych.

Jeżeli odległość punktu krzywej od pewnej prostej dąży do zera, oraz jest różna od zera przy oddalaniu się punktu do
lub
tzn. przy
lub przy
to prosta ta nazywa się asymptotą krzywej
.

RODZAJE ASYMPTOT

1. na to by przy
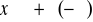
   prosta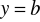
   była asymptotą krzywej ciągłej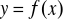
   , potrzeba i wystarcza, by granica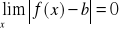
   oraz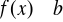
   co jest równoznaczne warunkowi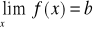
   oraz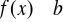
   

Wtedy prosta
nazywamy asymptotą poziomą krzywej

2. niech funkcja rzeczywista
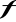
   będzie określona w pewnym otoczeniu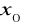
   
   ,
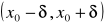
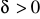
   z wyjątkiem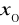
   

lub w przedziale

lub w przedziale

Mówimy, że krzywa
ma asymptotę pionową
gdy:

lub

lewostronną asymptotę pionową

lub

prawostronną asymptotę pionową

lub

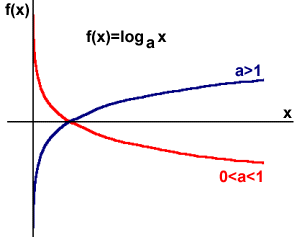
Krzywa
ma asymptotę pionową x=0 . Jest to asymptota prawostronna.

3. niech funkcja rzeczywista
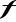
   będzie określona dla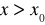
   
   
   

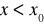
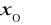
Mówimy, że prosta
jest asymptotą ukośną krzywej
przy

gdy:

,

Oraz

,

Twierdzenie 1

Niech funkcja rzeczywista
będzie określona dla

.

Prosta
jest ASYMPTOTĄ UKOŚNĄ krzywej
przy
wtedy i tylko wtedy, gdy istnieje skończona granica

oraz

Uwaga: Twierdzenie to zachodzi również gdy,