27.10.2009
Ciąg liczbowy jest to funkcja określona na zbiorze liczb naturalnych N. Oznaczamy tę funkcję symbolem (xn) przy czym xn![]()
n=1,2…
Jeżeli x>0 oraz ![]()
jest liczbą rzeczywistą to
![]()
gdzie Wn jest ciągiem liczb wymiernych zbliżonych do ![]()
.
Jeżeli
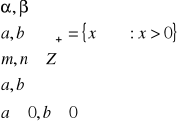
to
![]()
![]()
![]()
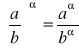
![]()
Funkcje trygonometryczne
Funkcje ![]()
, ![]()
są określone dla ![]()
,
przeciwdziedziną ![]()
, ![]()
jest Y=<-1,1>
Funkcja ![]()
jest określona dla
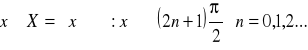
Funkcja ![]()
jest określona dla
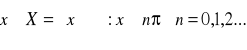
Przeciwdziedziną ![]()
jest ![]()
![]()
![]()
![]()
![]()
Odwrotnością funkcji trygonometrycznych sin x, cos x
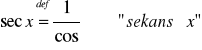
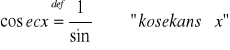
Funkcje cyklometryczne
Są to funkcje odwrotne do funkcji trygonometrycznych przy odpowiednim zawężeniu ich dziedziny.
![]()
WYKRES
![]()
WYKRES
![]()
WYKRES
![]()
WYKRES
Funkcja wykładnicza
![]()
Dziedziną f jest ![]()
Przeciwdziedziną jest zbiór
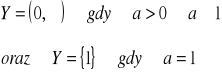
![]()
Oznaczmy ![]()
Jeżeli
![]()
to
![]()
Logarytmem dodatnim liczby b przy podstawie a , gdzie ![]()
jest wykładnik potęgi c do którego należy podnieść a , aby otrzymać b.
Jeżeli
![]()
to
![]()
![]()
![]()
Logarytm dziesiętny to logarytm przy podstawie ![]()
a=10 :
log b = c 10c=b
Logarytm naturalny to logarytm przy podstawie równej liczbie e.
przy czym 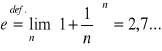
oznaczamy go symbolem
![]()
Prawa działań na logarytmach
Logarytm iloczynu
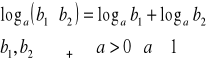
Logarytm ilorazu
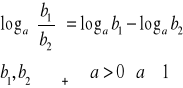
Logarytm potęgi
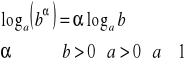
Zamiana podstawy logarytmu
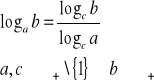
Funkcja logarytmiczna
Ponieważ funkcja wykładnicza ![]()
jest wzajemnie jednoznaczna dla a>0, a≠1 więc tylko wtedy posiada funkcje odwrotną.
Jest nią funkcja logarytmiczna
![]()
Funkcje hiperboliczne
![]()
![]()
![]()
![]()
gdzie 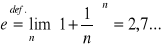
Wartość bezwzględna liczby rzeczywistej
Wartością bezwzględną lub modułem liczby rzeczywistej ![]()
nazywamy liczbę nieujemną ![]()
przy czym
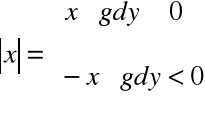
Własności:
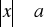
jest równoważna nierówności podwójnej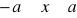
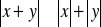

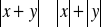

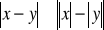
Funkcja wartości bezwzględnej (moduł)
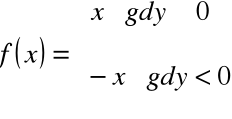
INDUKCJA ZUPEŁNA
Twierdzenie 1 - Zasada Indukcji Zupełnej
Niech każdej liczbie naturalnej n będzie przyporządkowane zdanie p(n)
Jeżeli :
zdanie p(1) jest prawdziwe
jeżeli zdanie p(n) jest prawdziwe, to zdanie p(n+1) jest prawdziwe,
to zdanie p(n) jest prawdziwe dla każdego n=1,2,3…
Wniosek:
Jeżeli
zdanie p(n) jest prawdziwe dla liczby całkowitej n0
z prawdziwości p(n) dla liczby całkowitej k wynika prawdziwość p(n) dla k+1, gdzie k≥n0
to zdanie p(n) jest prawdziwe dla wszystkich liczb całkowitych n≥n0
Przykład
Wykazać równość
![]()
Dowód. Zasada indukcji Zupełnej
dla n=1 mamy
p(1)
![]()
![]()
![]()
zakładamy, że istnieje
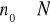
takie, że p(n0) jest prawdą tzn.
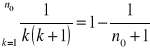
Wykażemy, że
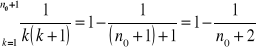
Kolejno otrzymujemy, wiedząc, że p(n0) jest prawdą
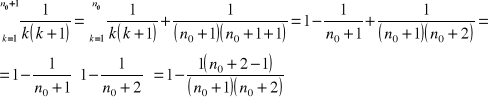
Na mocy indykcji powyższy wzór jest prawdziwy dla każdego naturalnego n.
36
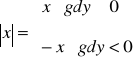
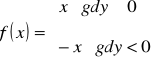
Wyszukiwarka
Podobne podstrony:
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
wszystkie wykłady z matmy stoiński - wersja na telefon, MATMA, matematyka
więcej podobnych podstron