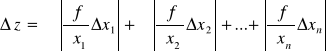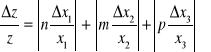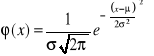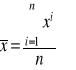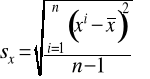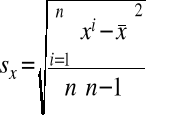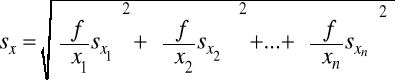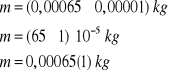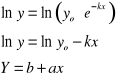PODSTAWOWE INFORMACJE O POMIARACH I NIEPEWNOŚCIACH POMIAROWYCH |
Celem zajęć w pracowni fizycznej jest pomiar wielkości fizycznych, analiza wyników pomiarów, obliczenie pewnej wielkości fizycznej, wyznaczenie niepewności pomiarowych oraz analiza (dyskusja) uzyskanych wyników. Pomiarem nazywamy cykl czynności prowadzących do uzyskania wartości wielkości mierzonej. Pomiary mogą być bezpośrednie i pośrednie (złożone). Pomiar bezpośredni dokonujemy przy pomocy jednego przyrządu pomiarowego np. linijki, stopera, wagi. W przypadku pomiaru pośredniego mierzymy bezpośrednio kilka wielkości fizycznych, a wyznaczaną wielkość obliczamy ze wzoru łączącego mierzone wielkości np. aby wyznaczyć opór opornika mierzymy bezpośrednio napięcie U i prąd I w obwodzie elektrycznym , a opór R wyznaczamy z prawa Ohma R=U/I.
Wynikiem pomiaru xd nazywamy wartość
Na ogół nie potrafimy obliczyć błędu Δx, ponieważ nie znamy dokładnej wartości xo a jedynie wartość Przyczyną błędów systematycznych, które powodują przesunięcie wartości mierzonych w górę lub w dół od wartości rzeczywistych może być np. używanie mało dokładnych przyrządów pomiarowych, zastosowanie uproszczonego wzoru. Błąd gruby może wynikać np. z błędnego odczytu z przyrządów pomiarowych i charakteryzuje się wyraźnym odstępstwem od innych wyników pomiaru. Podczas pracy w laboratorium zakładamy, że błędy systematyczne i grube potrafimy wykryć i wyeliminować. Według norm organizacji normalizacyjnych najważniejszym pojęciem w analizie wyników pomiarów jest obecnie niepewność pomiaru. Niepewność jest parametrem związanym z rezultatem pomiaru i charakteryzuje rozrzut wyników, który można w sposób uzasadniony przypisać wartości mierzonej*. Jednak podobnie jak błędy niepewności dzielimy na systematyczne i przypadkowe. W większości przypadków jeden z typów niepewności dominuje. Jeżeli przeważają niepewności systematyczne wtedy w serii pomiarów otrzymamy identyczne lub mało różniące się wyniki. Niepewności systematyczne wynikają głownie z dokładności przyrządów pomiarowych i niepewności odczytu przez obserwatora. Na niepewności przypadkowe (statystyczne) składa się wiele niezależnych przyczyn. Jeśli dominują niepewności przypadkowe wyniki pomiarów układają się symetrycznie wokół wartości rzeczywistej. W wielu przypadkach dawne pojęcia błędów systematycznych i przypadkowych pokrywają się z obecną definicją niepewności systematycznej i przypadkowej. Nie można całkowicie wyeliminować niepewności pomiarowych, ale można je zmniejszyć przeprowadzając np. większą ilość pomiarów i zastosowanie dokładniejszej aparatury pomiarowej. Stosownie do nowego podejścia do analizy niepewności pomiarowych wprowadzono następujące terminy(pojęcia):
Niepewności systematyczne (maksymalne) ocena typu B pomiarów bezpośrednich Wielkość niepewności systematycznej Δxs stanowi sumę niepewności wzorcowania przyrządu pomiarowego Δxw i niepewności odczytu przez obserwatora Δxo. Określenie dokładności przymiaru liniowego, suwmiarki, śruby mikrometrycznej nie nastręcza na ogół większych kłopotów. Nieco bardziej skomplikowane jest ocenianie dokładności mierników elektrycznych. W starszych miernikach wskazówkowych (mierniki analogowe) niepewność pomiaru wynika z klasy przyrządu. Jest to liczba niemianowana np. 0,5,1,2 podana na płycie czołowej miernika. Wyznacza ona niepewność systematyczną miernika Δxw obliczoną ze wzoru:
Za niepewność systematyczną odczytu przyjmujemy wartość 0,5-1 działki elementarnej. Maksymalną niepewność systematyczną obliczamy jako sumę : Δxs= Δxw+ Δxo (0.3)
zakładając, że niepewności pomiarowe nie kompensują się, a zawsze dodają się do siebie. Niepewność systematyczną mierników cyfrowych podaje producent określając zarówno rozdzielczość jak i dokładność pomiaru. Najczęściej niepewność Δxs zapisujemy w postaci: Δxs=…% odczytu wartości mierzonej +…% zakresu lub Δxs=…% odczytu wartości mierzonej +n cyfr na ostatnim miejscu . Wyznaczoną niepewność systematyczną Δxs nazywamy niepewnością maksymalną. Wartość mierzona mieści się w przedziale (x-Δxs, x+Δxs). Eksperymentator może założyć, że wszystkie wartości wewnątrz tego przedziału są jednakowo prawdopodobne(prawdopodobieństwo p=1). Prowadzi to do przyjęcia prostokątnego (jednostajnego) rozkładu prawdopodobieństwa, według, którego niepewność standardowa u(x) oszacowana metodą B wynosi:
Wykonujący doświadczenie może oczywiście posłużyć się innym rozkładem prawdopodobieństwa, ale opisując wyniki doświadczenia powinien podać sposób wyznaczenia u(x). Niepewność systematyczna pomiarów pośrednich Metoda różniczki zupełnej Przy pomiarach wielkości fizycznych zdarza się, że jest ona obliczana na podstawie kilku wielkości zmierzonych bezpośrednio x1 , x2,...xn . Np. aby wyznaczyć wartość przyśpieszenia ziemskiego za pomocą wahadła matematycznego mierzymy bezpośrednio długość wahadła l i jego okres T. Każda z tych wielkości zmierzonych bezpośrednio jest obarczona niepewnością pomiarową oznaczoną odpowiednio Δx1, Δx2,...,Δxn. W celu znalezienia niepewności Δz wielkości złożonej z = f(x1,x2,...,xn) stosuje się rozwinięcie funkcji wielu zmiennych w szereg Taylora. Przy ograniczeniu szeregu do dwóch pierwszych wyrazów rozwinięcia otrzymujemy wzór na maksymalną niepewność systematyczną, wielkości mierzonej pośrednio:
Symbol Wartości bezwzględne pochodnych cząstkowych oznaczają, że wszystkie niepewności pomiarowe zawsze się dodają, a nie ulegają kompensacji, gdy np. obliczona wartość jednej z pochodnych przyjmuje wartości ujemne. Opisaną powyżej metodę wyznaczania Δz nazywamy metodą różniczki zupełnej. W przypadkach, gdy funkcja z ma postać iloczynu lub ilorazu dowolnych potęg zmiennych x w postaci:
gdzie A, n, m, p s* sta*ymi, metoda różniczki zupełnej prowadzi do prostej zależności pozwalającej wyznaczyć maksymalną niepewność względną Δz/z wielkości złożonej. Po obliczeniu różniczki zupełnej biorąc wartości bezwzględne otrzymujemy wzór :
Wzór na maksymalną niepewność systematyczną, Δz otrzymamy mnożąc powyższe równanie przez otrzymaną doświadczalnie wartość z. Dla więcej niż 3 zmiennych prawa strona równania będzie odpowiednio dłuższa.
Niepewności przypadkowe. Ocena typu A pomiarów bezpośrednich
Jeżeli w serii pomiarów zaobserwujemy, że kolejne wyniki nie dają identycznych wartości, a nieco się różnią zakładamy, że występują niepewności przypadkowe (statystyczne).Rozrzut wyników podlega pewnym rozkładom statystycznym, z których najbardziej znany jest rozkład Gaussa (rozkład normalny).Rozkład częstości występowania niepewności przypadkowych w dużej serii pomiarów opisuje funkcja Gaussa:
φ(x)—oznacza gęstość prawdopodobieństwa, μ- wartość oczekiwaną rozkładu, σ -odchylenie standardowe rozkładu. Dla x=μ funkcja φ(x)osiąga maksimum. Parametr μ jest wielkością oczekiwaną rozkładu i jest to na ogół wartość średnia wartość z n pomiarów. Odchylenie standardowe σ w rozkładzie Gaussa oznacza, że wartość rzeczywista lub jej przybliżenie
Rozkład Gaussa dotyczy nieskończonej liczby pomiarów i jest opisany funkcja ciągła. Dla skończonej liczby n pomiarów jako wynik końcowy przyjmujemy średnia arytmetryczną
gdzie n oznacza ilość pomiarów, xi-wynik i-tego pomiaru Miarą niepewności i-tego pomiaru jest odchylenie standardowe pojedynczego pomiaru sx:
(0.10)
Niepewnością przypadkową wartości średniej
Można zauważyć, że:
Odchylenie standardowe wielkości średniej standardową σ występującą w rozkładzie Gaussa.
Niepewności statystyczne wielkości złożonych - prawo przenoszenia wariancji
Niepewności statystyczne wielkości złożonych otrzymujemy z prawa przenoszenia wariancji. Wzór na odchylenie standardowe wartości średniej
z = f(x1,x2,...,xn) zapisujemy następująco:
gdzie W praktyce laboratoryjnej zdarzają się przypadki, gdy niepewności systematyczne i przypadkowe są porównywalnej wielkości. Dokładne metody obliczenia sumy obu niepewności są opisane w literaturze. W metodzie uproszczonej do maksymalnej niepewności systematycznej dodajemy potrojoną wartość odchylenia standardowego niepewności statystycznej. Prowadzi to jednak do zawyżenia niepewności pomiarowych Podczas wykonywania ćwiczeń w pracowni fizycznej częściej jednak, z braku czasu wykonujemy pojedyncze pomiary, co prowadzi do oceniania tylko niepewności systematycznych. Sposoby zapisu wyników pomiarowych i ich niepewności
Końcowe wyniki pomiarów podajemy w układzie SI, chociaż często bezpośredni odczyt następuje w innym układzie jednostek np. centymetry, gramy, miliampery itp. Wyniki pomiarów zaokrąglamy do tego samego miejsca po przecinku (dziesiętnego),do którego zaokrąglaliśmy niepewność pomiarową. Zarówno wynik jak i niepewność pomiarowa muszą być zapisane w tej samej postaci. Przy pomiarze masy miedzi osadzonej w wyniku elektrolizy siarczanu miedzi użyto wagi elektronicznej o niepewności systematycznej (uchyb) Δm=0,01g.W wyniku elektrolizy osadziła się masa m=0.65 g. Wynik pomiaru możemy napisać w następujący sposób:
W powyższym przykładzie wynik zapisano z dokładnością do dwóch cyfr znaczących. W praktyce laboratoryjnej w zapisie końcowego wyniku rozsądne jest ograniczenie się do 3-4 cyfr znaczących. Jeśli przy obliczeniach kalkulatorem lub arkuszem kalkulacyjnym otrzymujemy wynik zawierający wiele cyfr znaczących np. 3,1415927 to zapisujemy go w postaci 3,14 lub 3,142. Zaokrąglenia dokonujemy dopiero w wyniku końcowym, a nie w wynikach pomiarów bezpośrednich. W celu wyznaczenia prostokątnej powierzchni pracowni fizycznej zmierzono jej długość a i szerokość b. Otrzymano :
W wyniku mnożenia otrzymano pole powierzchni P:
Ponieważ zaokrąglenia dopiero w wyniku końcowym powstaje pytanie, z jaką dokładnością możemy zapisać wynik końcowy wraz z niepewnością. Wynik końcowy powinien być zapisany z taką samą lub mniejszą ilością cyfr znaczących niż najmniej dokładny wynik pomiaru. Szerokość b została zmierzona z dokładnością do 3 cyfr znaczących i tyle cyfr zapiszemy w końcowym wyniku.
Niepewność systematyczna maksymalna wyznaczona metodą różniczki zupełnej wynosi ΔP=0,88995 m2.Jednak ΔP zapisujemy z tą samą ilością miejsc dziesiętnych, co wynik pomiaru. Końcowy wynik można zapisać w postaci:
Możemy również zapisać niepewność względną pomiaru ΔP/P i wyrazić ją w procentach: ΔP/P=2%, a wynik końcowy zapisać w postaci:
Wykonywanie wykresów i graficzna analiza funkcji liniowej.
Wyniki pomiarów na ogół przedstawiamy na wykresie y=f(x) Bezpośrednio mierzone wartości nie zawsze są nanoszone na wykres, jeżeli funkcja opisująca dane zjawisko fizyczne jest złożona np. wykres zależności kwadratu okresu T2 od długości l wahadła matematycznego. W tabeli pomiarowej zapisujemy pary punktów (xi,yi), gdzie i=1,2,3…n. powstałe w wyniku pomiarów bezpośrednich oraz,jeśli to konieczne, pary punktów powstające w wyniku odpowiedniego przekształcenia matematycznego danych pomiarowych. Wykresy sporządzamy na papierze milimetrowym twardym ostro zaostrzonym ołówkiem. Niezbędne przyrządy to także linijka, gumka i komplet krzywików. Wykonywanie wykresu
Badanie funkcji liniowej.
Wiele zjawisk fizycznych można opisać za pomocą funkcji liniowej lub funkcji, która po przekształceniu i zamianie zmiennych staje się funkcją liniową. Funkcją tego typu jest np.malejąca funkcja wykładnicza
(0.14) (0.15) (0.16)
gdzie Y=lny ,b=lnyo, a=-k.
Podstawienia zmiennych prowadzące do otrzymania funkcji liniowej można dokonać także w przypadku innych funkcji. Takie podstawienia nazywamy linearyzacją. Parametry funkcji liniowej y=ax+b możemy wyznaczyć bezpośrednio z wykresu prowadząc przewidywaną prostą przez największą ilość niepewności pomiarów. Wyraz wolny b odczytujemy z przecięcia prostej z osią y. Współczynnik kierunkowy a obliczamy jako iloraz przyrostu funkcji Δy do przyrostu zmiennej niezależnej Δx :
współczynnik a prawie nigdy nie jest tangensem kąta nachylenia prostej (kąta, który można odczytać z wykresu),ponieważ przeciwnie niż w matematyce skale na osi x i y oznaczają wartości wielkości fizycznych wraz z podaną jednostką. Bardziej obiektywną metodą wyznaczenia parametrów a i b równania prostej jest wykorzystanie metody najmniejszych kwadratów. W wyniku pomiarów otrzymujemy pary punktów (xi,yi), gdzie i=1,2,3…n. które chcemy opisać funkcją t=ax+b. Metoda najmniejszych kwadratów zakłada obliczenie takich parametrów a i b, aby suma kwadratów różnic wartości doświadczalnych yi i ti była jak najmniejsza:
Warunkiem koniecznym istnienia minimum funkcji S(a,b) jest zerowanie się pochodnych cząstkowych:
Po obliczeniu pochodnych otrzymujemy układ dwóch równań, z których wyznaczmy parametry a i b Z praw statystyki matematycznej otrzymujemy też wzory na odchylenia standardowe a i b oraz współczynnika korelacji Pearsona r. Współczynnik korelacji r przyjmuje wartości z przedziału <-1,1>.Im bardziej |
|
8
7
6
Wyszukiwarka
Podobne podstrony:
ćw.14, Fizyka, Skrypt do Laborek
ćw.8, Fizyka, Skrypt do Laborek
ćw.27, Fizyka, Skrypt do Laborek
ćw.24, Fizyka, Skrypt do Laborek
ćw.31, Fizyka, Skrypt do Laborek
ćw.3, Fizyka, Skrypt do Laborek
ćw.20, Fizyka, Skrypt do Laborek
ćw.15, Fizyka, Skrypt do Laborek
ćw.7, Fizyka, Skrypt do Laborek
1 Strona tytułowa, Fizyka, Skrypt do Laborek
ćw.12, Fizyka, Skrypt do Laborek
ćw.26, Fizyka, Skrypt do Laborek
ćw.23, Fizyka, Skrypt do Laborek
ćw.25, Fizyka, Skrypt do Laborek
ćw.5, Fizyka, Skrypt do Laborek
ćw.13, Fizyka, Skrypt do Laborek
ćw.17, Fizyka, Skrypt do Laborek
ćw.11, Fizyka, Skrypt do Laborek
ćw.21, Fizyka, Skrypt do Laborek
więcej podobnych podstron