088 089

88 Damian Salęga. Tomasz Zuchowicz

Pewne komplikacje powstają w sytuacji, gdy funkcja F jest funkcją niejednoznaczną. Wtedy równanie (5.3) jest niejednoznaczne i może prowadzić do kilku rozwiązań nakładających się na siebie w efekcie czego otrzymamy kilka trajektorii przechodzących przez jeden punkt osobliwy lub punkt leżący w^; obszarze niejednoznaczności.

5.3. Płaszczyzna fazowa układu liniowego [2], [3], [4], [5]

W przypadku układu liniowego równania (5.2) przyjmą następującą formę:

dx

dt

- X-,

(54)

dx₇

0*! +^a\^X2

co odpowiada równaniu różniczkowemu drugiego rzędu dla zmiennej X\ = x

d²x

dr

dx

^a'~d~^a°^{x = 0}

(5.5)

Jeśli ^ 0 to jedynym punktem osobliwym jest punkt x\=x₂ = 0, zaś charakter rozwiązań jest określony przez w^rartości własne układu, czyli przez w'artości własne macierzy współczynników równań (5.4)

0	1
	«i

(5.6)

Wartości własne są pierwiastkami równania charakterystycznego w postaci:

(5.7)

czvli:

A² ~ a, A - a, = 0

(5.8)

Pierwiastki te są równe

A

a

Oj

2

+ a

o

(5.9)

* Rozpatrzmy teraz dwa warianty rozwiązań. Pierwszy dla wartości własnych £ rzeczywistych gdy a_x² > - 4a₀, drugi dla wartości własnych zespolonych sprzężonych, gdy a² < - 4#₀*

1. Wartości własne rzeczywiste:

a) A] < 0, A₂ < 0 obydwie wartości własne są ujemne, punkt osobliwy nazywa się węzłem stabilnym.

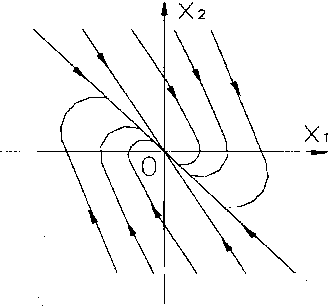
Rys 5.2. Wykres węzła stabilnego

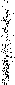
b) Ai > 0, A2 > 0 obydwie wartości własne są dodatnie, punkt osobliwy nazywa się węzłem niestabilnym.

Rys. 5.3..Wykres węzła niestabilnego