068 3

68 Modelowanie dynamiki obiektów sterowania

s,. s₂,.... s_r. przy czym krotność poszczególnych pierwiastków oznaczymy

?^J

jako rn_k (a więc spełniony jest warunek: ^ m_k = n). Ogólny wzór, określający

k-\

oryginał transformaty (8.28), jest następujący:
(8.29)	r w;, i a /(*)=£ E^r^l'^e"^v A-I l=- 0 '•
gdzie:
(8.30)	l i	(s-h)
	(mk-\-l)\ ds^nlk-^l~'

»n L(s) M(s)

Przykład 8.4. Przeprowadzimy obliczenia sprawdzające dla danych jak w przykładzie poprzednim. Transformata:

(8.31)

F(s) =

s + 3

(,s + l)(y+2)²

ma dwa pierwiastki rzeczywiste: s_l~— 1, s₂=-2. Pierwiastek s_Y ~ -1 jest pojedynczy-\. natomiast pierwiastek s₂ ~ -2 jest podwójny. Zatem w rozpatrywanym przypadku: r = 2, m_[ - 1, m₂~ 2. Wzór (8.29) przyjmuje więc postać:

(8.32)

/w-—

0!

t°e-‘

+    ^{°^e ' ⁺ ~~ Ą.o^e ' + Ą,o^e ‘ + Ą.\ te "

gdzie:

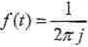
gdzie: s,,5₂.....s_r

res F(s)e^sl

<7 /JG

k=i

, r> 0.

- pierwiastki wielomianu M(s). Residuum funkcji F(s) =

b(S)

M(s)

w

punkcie s - S/. oblicza się następująco:

res F(s)e^st

S^-Sl

1

d^mt'

(™k -1)1 ds^m>:

-l

Stosując wzór Leibniza na pochodną iloczynu, uzyskuje się postać (S.29)-(8.30). Szczegółowe wyprowadzenia zawiera większość podręczników traktujących o rachunku operatorowym.