090 2
90 Modelowanie dynamiki obiektów sterowania
Wynik ten można zaobserwować doświadczalnie, obserwując odpowiedzi układu inercyjnego na ciąg impulsów o postaci (10.1). Wykresy odpowiedzi układu inercyjnego na te impulsy oraz odpowiedź impulsową przedstawiono na rys. 10.2 (do obliczeń przyjęto k = 1, T = 0.2 fs]).
90 Modelowanie dynamiki obiektów sterowania
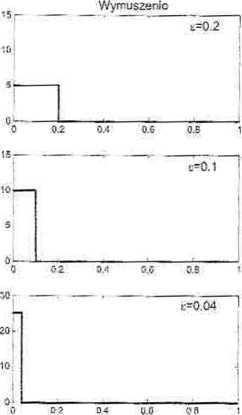
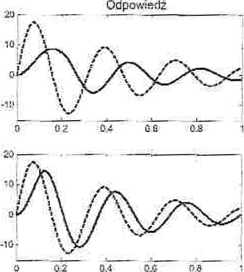
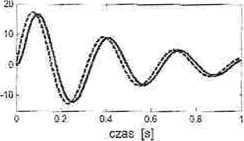
Rys. 10.3. Odpowiedzi układu oscylacyjnego na impulsy prostokątne (linia przerywana - odpowiedź impulsowa)
Transmitancja układu oscylacyjnego jest następująca:
H(s) =
gdzie: k - współczynnik wzmocnienia układu oscylacyjnego, 2nT - okres drgań własnych nietłumionyck, (Te (0,1) - współczynnik tłumienia. Po przekształceniu funkcji H(s) do postaci:
(10.9)
|
f 0 |
2 |
,/i^F |
|
s + — |
+ | |
|
V TJ |
T |
Wyszukiwarka
Podobne podstrony:
040 3 40 Modelowanie dynamiki obiektów sterowania t (5.7) y{1) - F(u)(l) =
042 4 42 Modelowanie dynamiki obiektów sterowania 42 Modelowanie dynamiki obiektów sterowania (6.2)
44 Modelowanie dynamiki obiektów sterowania Otrzymamy: X (6.12) y(t )=
050 4 50 Modelowanie dynamiki obiektów sterowania Przyjmiemy, że znana jest wartość początkowa x(V0)
054 2 54 Modelowanie dynamiki obiektów sterowania (7.18) x(/ + rWv,W)x(o) Podobnie
056 3 56 Modelowanie dynamiki obiektów sterowania równania (7.29) x(f)= Ax(/) opis
058 3 58 Modelowanie dynamiki obiektów sterowania Łatwo spostrzec, że pierwszy składnik stanowi skła
060 5 60 Modelowanie dynamiki obiektów sterowania Zjawiły się słowa, języki. prawa, nauki i sztuki p
062 4 62 Modelowanie dynamiki obiektów sterowania Tabl. 8.2 Przykłady transformat Laplace’a
064 4 64 Modelowanie dynamiki obiektów sterowania Wielomian występujący vr mianowniku ma trzy pierwi
068 3 68 Modelowanie dynamiki obiektów sterowania s,. s2,.... sr. przy czym krotność poszczególnych
074 3 74 Modelowanie dynamiki obiektów sterowania układu. Strumień y(t) wypływającej wody z drugiego
076 2 76 Modelowanie dynamiki obiektów sterowania W wyniku zastosowania przekształcenia Laplace a do
078 3 78 Modelowanie dynamiki obiektów sterowania W sposób analogiczny wyznaczamy transmitancję równ
S2 Modelowanie dynamiki obiektów sterowania Rozpatrywany układ nie jest układam oscylacyjnym. Po wyl
092 2 92 Modelowanie dynamiki obiektów sterowania Ostatnia zależność dla układów przyczynowych (h(t)
98 Modelowanie dynamiki obiektów sterowania 98 Modelowanie dynamiki obiektów sterowania />0 (11.2
048 2 48 Modelowanie dvnamiki obiektów sterowania Zagadnienie powyższe przyjmuje też formą zagadnien
080 2 80 Modelowanie chnainiki obiektów sterowania (9.28) H(s) = k T2s2 + 2 ą’s +1 Układ opóźniający
więcej podobnych podstron