10 (47)

198

9. Funkcje w ielu zmiennych

Zatem £ b,_ka_kj =    lub

(91)

Ponieważ B jest odwracalne, więc det [B] / 0. Na mocy (91) i twierdzenia 9.35 widzimy, że

(92)

det[zł]_w = det [zł].

Dlatego wyznacznik operatora liniowego nic zależy od wyboru bazy, w której wyrażona jest macierz tego operatora. Zatem ma sens mówienie o wyznaczniku operatora liniowego, nie mając przy tym na myśli żadnej określonej bazy.

9.38. Jakobiany. Jeśli f odwzorowuje zbiór otwarty EcR" w R" i f jest różniczkowalne w punkcie x e E, to wyznacznik operatora liniowego f(x) nazywamy jakobianum odwzorowania f w punkcie x. Jakobian ten oznaczamy JĄ\). A więc

(93)

Jj(x) = det f'(x).

Dla oznaczenia ,/_f(x) będziemy także używać symbolu

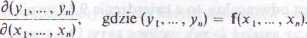
(94)

Posługując się pojęciem jakobianu, podstawowy warunek twierdzenia o funkcji odwrotnej można zapisać następująco: ./_f(a) # 0 (porównaj twierdzenie 9.36). Jeśli twierdzenie o funkcji uwikłanej sformułujemy w terminach funkcji (59), to założenie tego twierdzenia sprowadza się do nierówności

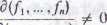
C[x_x,..., x„)

Pochodne wyższych rzędów

9.39. DEFINICJA. Niech / będzie funkcją rzeczywistą określoną na otwartym podzbiorze E przestrzeni R", i posiadającą pochodne cząstkowe DJ,..., D„f Jeżeli funkcje Djf są same różniczkowalne, to pochodne cząstkowe drugiego rzędu definiujemy jako

£>,/= D,Djf (i,j= 1,

Jeżeli wszystkie funkcje D^/są ciągłe w E, to powiemy, że f jest klasy W w E lub inaczej, że f e e <6"(E).

Odwzorowanie f z E do R^m jest klasy ^".jeżeli każda jego składowa jest klasy ^<€".

Może zdarzyć się, że Dljf # DjJ w pewnym punkcie, mimo że obie pochodne istnieją (zobacz zadania 27). Niemniej jednak, jak zobaczymy poniżej, Dyf— DjJ, jeżeli tylko obie te pochodne są ciągłe.

Dła uproszczenia (i bez utraty ogólności) sformułujemy następne dwa twierdzenia dla funkcji rzeczywistych dwu zmiennych. Pierwszym z nich jest twierdzenie o wartości średniej.