img050

108 lf. Parametryczne testy istotności

2 kolei obliczamy sumy kwadratów: dla zmienności całkowitej

(2*20)    SK_C= £ £(*,,-*)•,

i« 1 j= 1

dla zmienności między wierszami Iczynnik A)

(2.21)    SK„ = »r t (i,.-5>²,

1=1

dla zmienności między kolumnami (c2vnnik B)

k

(2.22)    SK*=r £ (X-,—x)\

;=i

dla zmienności reszto wej

(2.23)    SK„= t X(x_i;-i,.-i.,+3B)²=SK_c-SK^-SK,.

1=1    1

Dzieląc sumy kwadratów (2,21), (2.22), (2.23) przez odpowiadające im stopnie swobody, otrzymujemy wariancje z próby będące estymatorami wariancji a² populacji. Wariancje z próby są podstawą obliczenia wartości statystyki F, zgodnie z następującą tablicą analizy wariancji:

Źródło zmienności	Suma kwadratów	Stopnie swobody	■Wariancja	Test F
między wierszami (czynnik A)	SK,	r-1	ii	F = U * A a) Ja
między- kolumnami (czyjmik 5)	SK#	A-]	sl
rdziowa | tbłąd losowy)	sk*	(r— 1) (/c— 1)

Gdy hipoteza H₀ jest prawdziwa, wtedy statystyka F_A ma rozkład F Snede-cora o (r— 1) i (r-l) (k-1) stopniach swobody, natomiast statystyka F₉ ma wtedy rozkład FSnedecora o (k— 1) i (r-1) {k—1) stopniach swobody.

Obliczone w tablicy wartości statystyk F_A i f₀ porównujemy z odczytanymi 7. tablicy rozkładu F Snedecora wartościami krytycznymi F_Ak i F_Si€ dla przyjętego poziomu istotności a i odpowiednich liczb stopni swobody.

Jeżeli zachodzi nierównośćF_A^F_AtXi to hipotezę //₀ odrzucamy (co oznacza wykazanie istotnego wpływu czyni)ika A w doświadczeniu). Podobnie, jeżeli    to hipotezę H₀ odrzucamy (oznacza to wyka

zanie istotnego wpływu czynnika B w przeprowadzanym doświadczeniu). Jeżeli zachodni F_A<F_{A a} lub F_B<F_B „ to nie udowodniono istotnego wpływu danego czynnika.

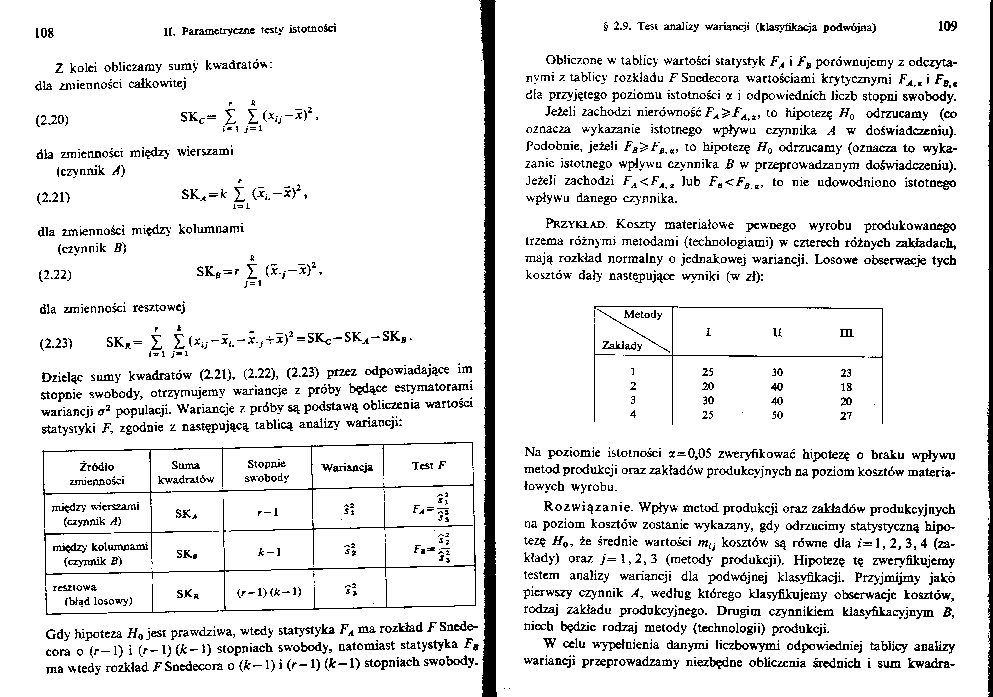
Przykład Koszty materiałowe pewnego wyrobu produkowanego trzema różnymi metodami (technologiami) w czterech różnych zakładach, mają rozkład normalny o jednakowej wariancji. Losowe obserwacje tych kosztów dały następujące wyniki (w zł):

\ Metody	I	U	m
Zakiady \s
1	25	30	23
2	20	40	18
3	30	40	20
4	25	50	27

Na poziomie istotności cc=0,05 zweryfikować hipotezę o braku wpływu metod produkcji oraz zakładów produkcyjnych na poziom kosztów materiałowych wyrobu.

Rozwiązanie. Wpływ metod produkcji oraz zakładów produkcyjnych na poziom kosztów zostanie wykazany, gdy odrzucimy statystyczną hipotezę łf_Q, że średnie wartości m_ti kosztów są równe dla i= 1,2, 3, 4 (zakłady) oraz >=1,2,3 (metody produkcji). Hipotezę tę zweryfikujemy testem analizy wariancji dla podwójnej klasyfikacji. Przyjmijmy jako pierwszy czynnik A, według którego klasyfikujemy obserwacje kosztów, rodzaj zakładu produkcyjnego. Drugim czynnikiem klasyfikacyjnym B, niocb będzie rodzaj metody (technologii) produkcji.

W celu wypełnienia danymi liczbowymi odpowiedniej tablicy analizy wariancji przeprowadzamy niezbędne obliczenia średnich i sum kwadra-