Photo006

Ekonometria Współczesna

Jvar(a₀) = S(a₀),

V^var(a,) =S(tf,),

Jv&r(a_K)=S(a_K).

Średnic błędy ocen parametrów przy oszacowanej postaci modelu zapisuje się w następujący sposób:

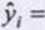
^ao + ^a\ ^xu S(a₀) 5(o,)

+ °2 ^X21 S(a₂)

+

a_K x S(a_K)

Ki »

(3.17)

gdzie:

y. - oszacowane wartości zmiennej objaśnianej Y> x_kl - obserwacje na zmiennej objaśniającej X_k, a₀ - ocena wyrazu wolny, a_k - oceny parametrów strukturalnych modelu,

S(a_k)- średnie błędy ocen parametrów strukturalnych.

Interpretacja średnich błędów ocen parametrów:

Szacując parametry strukturalne modelu na podstawie N-clcmentowcj próby, mylimy się średnio o S(a_k) w stosunku do oceny parametru a_k.

Własności estymatora klasycznej MNK

ZGODNOŚĆ

Estymator K.MNK dany wzorem: a = (X^TX)~* X^Ty

jest estymatorem zgodnym, jeżeli spełniony jest następujący warunek:

plim(fl) = a. Powyższy zapis jest tożsamy z zależnością postaci: »-»»

p lim(a - a) = O.

n->co

Estymator średnich błędów ocen parametrów KMNK dany jest wzorem:

Var(a - a) = S* (x^Tx) '

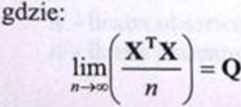
(Q jest macierzą skończoną i nicosobliwą),

lim Var(a - a) = lim — - =0Q ¹ =0.

stąd wynika następująca zależność:

nieobciążoność

Estymator KMNK dany wzorem jest estymatorem nicobciążonym, jeżeli spełnia warunek postaci:

E (a) = a

Z założeń klasycznej MNK:

E(X_k, e) = 0    (zmienne objaśniające nie są skorelowane ze składnikiem

losowym),

£(e) = 0 (wartość oczekiwana składnika losowego jest równa zero), wynika, że wartość oczekiwaną z estymatora można wyrazić zależnością postaci:

E(a) = e|x^tx) ' X^TyJ= e[(x^tx)'' X^T(x^Ta + e)]=... = e[b + (x^Tx)^-' X^te|= = o + e[(x^tx)'' X^te = o + (x^Tx)'‘ X^tE(e) = o

EFEKTYWNOŚĆ

Estymator KMNK jest estymatorem efektywnym, jeżeli spełniony jest następujący warunek:

D²(a) = V(a) = S²(X^TX)”' -> min

Estymator KMNK jest najlepszym estymatorem w klasie estymatorów liniowych i nicobciążonych, jeżeli istnieje taka macierz A dana wzorem:

A = V(a")-V(a), gdzie:

Macierz A jest macierzą określoną nieujemnic (lub dodatnio półokrcśloną), jeżeli

V(a")- macierz wariancji-kowariancji każdego innego estymatora rozważanej klasy.

elementy na głównej przekątnej tej macierzy są większe lub równe zero, tj. ^var(^a* ") - var(o,) > 0

gdzie:

var(a_Jl") - odpowiednie wariancje estymatora a" , var(<7*) - odpowiednie wariancje estymatora a.

55