Photo019

Ekonometria Współczesna

wartości krytyczne wynoszą odpowiednio:

a - *0,025 > 2

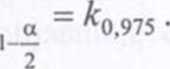
Jeżeli wartość k znajdzie się w przedziale k_a<k<k _a, wówczas nie m«

7    '"7

podstaw do odrzucenia hipotezy zerowej H₀ . Stwierdza się, że reszty modelu mają charakter losowy, model ma postać liniową. Natomiast jeżeli wartość k znajdzie się w przedziałach k < k_a lub k > k _a , wówczas odrzuca się hipotezę zerową

I    ^1_7

H₀ na rzecz hipotezy alternatywnej //,. Stwierdza się, że reszty nie mają

charakteru losowego, model nie ma postaci liniowej. W takiej sytuacji należy wybrać inną postać analityczną i oszacować model ponownie.

Badanie losowego charakteru reszt za pomocą testu serii („Runs test") w programie Gretl przedstawiono szczegółowo w rozdziale 5.2. „Runs test" oparty jest na parametrze R (liczba serii k), o rozkładzie normalnym z parametrami R ~ N(\i_R\a_R). Wartość statystyki z standaryzowanego rozkładu normalnego dana jest wzorem:

gdzie:

(4.13)

x_R - estymator wartości oczekiwanej parametru R wyznaczony ze wzoru:

N

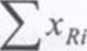
(4.14)

s_R - estymator odchylenia standardowego parametru R wyznaczony z wzoru.

N

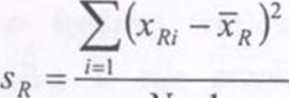
N-1

(4.15)

Wartość krytyczną z_(ł odczytuje się z tablic rozkładu normalnego, przy pozio j istotności a = 0,05 wynosi ona:

, ,*=1,96.

^■Tfjość |z|<z_a. wówczas nic ma podstaw do odrzucenia hipotezy zerowej 7t\ badanego modelu mają charakter losowy, model ma postać liniową. ⁰ miast jeżeli |z|>z„, to odrzuca się hipotezę zerową H₍₎ na rzecz hipotezy tywnej . Stwierdza się nielosowy charakter reszt, model nic ma postaci

liniowej.

. Badanie normalności rozkładu składnika losowego

*T»»'**^-*

W niniejszym podrozdziale do zbadania zgodności rozkładu składnika losowego rozkładem normalnym wykorzystano statystykę Bery i Jarque’a\ Badanie polega na porównaniu rozkładu składnika losowego z próby z postulowanym,

teoretycznym rozkładem normalnym.

Hipotezy zerowa i alternatywna są następujące:

H_lt: F(e_i) = F_N(e_i) (rozkład składnika losowego jest rozkładem normalnym)

//,: F(e,) * F_n(e,) (rozkład składnika losowego nie jest rozkładem normalnym)

Rozkład statystyki Bery-Jarquea (JB) jest zbieżny do rozkładu chi-kwadrat o 2 stopniach swobody: X«(2) ■ Statystyka Bery-Jarque’a ma wówczas postać:

\

(4.16)

gdzie:

1 *

1=1

i=l

e, - reszty modelu,

S(e_f) - standardowy błąd reszt.

Ipowy^: ^a5o^Cs^rnalywny^m J^{est lest} zgodności chi-kwadrat, wymaga on jednak dużej liczebności próby ^vv P^ypadku mniejszej próby lepiej jest stosować test Bery-Jarque'a.