skanuj0062 (Kopiowanie)

Substancja

Ryc. 8.9. Otwarty model jedno-kompartmentowy dla wlewu dożylnego

w organizmie

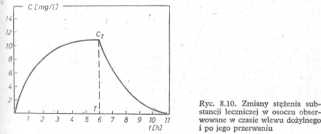
którego ograniczymy omawianie tego problemu, przedstawiono na ryc. 8.9, a przebieg zmian stężenia leku w osoczu w czasie wlewu i po jego przerwaniu na ryc. 8.10. Jeżeli wprowadzoną dawkę leku oznaczy się przez D, a czas trwania wlewu przez T, to stosunek:

k„ = DIT

mający wymiar masa/czas i określający szybkość wprowadzania leku do organizmu, będzie stałą szybkości dla procesu wlewu. Szybkość zmian stężenia substancji leczniczej w osoczu, będąca wypadkową szybkości wprowadzenia leku do organizmu i jego eliminacji, określa równanie*:

Scalkowanie tego równania daje następujące wyrażenie na stężenie substancji leczniczej w osoczu w czasie t spełniającym warunek t < T:

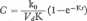
(8.37)

Z równania tego wynika, że stężenie substancji leczniczej podczas wlewu zwiększa się wykładniczo do wartości granicznej:

zależnej, jak wynika z równania 8.38, od stałej szybkości wlewu (kp) i od klirensu. W praktyce czas, po którym lek osiąga 95% tego silenia, jest równy ok. 4 biologicznym okresom półtrwania.

Przerywając wlew w czasie t = T, powoduje się zmniejszenie stężenia (ryc. 8.10). Ponieważ w tym czasie C =Ct, można napisać:

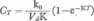
(8.39)

* k„ musi być podzielone przez Vd, ponieważ wyrażane jest w jednostkach masa/czas, podczas gdy iloczyn K • C w jednostkach masa/objętość • czas.

122 Zarys biofarmacji

Dla czasu t > T przebieg stężenia można opisać równaniem:

C = Cre-^K(-D    (8.40)

Z teoretycznego punktu widzenia długotrwały wlew dożylny pozwala na dokładne wyznaczenie parametrów farmakokinetycznych dla tych leków, których nie można podać drogą szybkiego wstrzyknięcia dożylnego, a w praktyce klinicznej umożliwia uzyskanie stacjonarnego stężenia substancji leczniczej w osoczu przez cały czas trwania wlewu.

Sposób posługiwania się równaniami 8.37-8.40 wyjaśnia następujący przykład.

Przykład

W tabeli niżej podano stężenie substancji leczniczej w osoczu zmierzone w czasie trwania wlewu dożylnego prowadzonego z prędkością k„ = 50mg/'h oraz po jego przerwaniu.

Stężenie

[mg/h]

W czasie trwania wlewu 3,9 6,3 8,6 9,5 9,8

Po przerwaniu wlewu <5,9 3,61 .133 (''0,49^>

0,07

Narysować półlogarytmiczny wykres zmian stężenia, obliczyć stalą szybkości eliminacji, biologiczny okres póltrwania, klirens i objętość dystrybucji tej substancji leczniczej.

Dożylne podawanie substancji leczniczych 123