UNTITL66

Rozszyfrować rynek

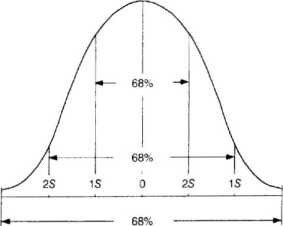
Diagram 4.18 Procentowy rozkład zmiennej w rozkładzie normalnym przy S =1-3. gdzie S stanowi odchylenie standardowe.

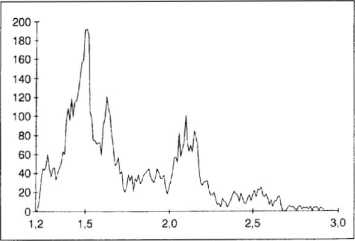
Diugram 4.19 Rozkład częstotliwości kursu CHF/USD (w Europie) w latach 1985-1994. Oś .< oznacza kurs zamknięcia CHF/USD w Europie, natomiast oś y oznacza jego częstotliwość.

Wariancja i odchylenie standardowe

W celu dokonania pomiaru rozproszenia lub zmienności danych w stosunku do ich średniej lub wartości środkowej obliczamy poniż sze wyrażenie:

Hx-u)/n

gdzie a oznacza zmienną, u średnią, natomiast n liczebność próby. Ale skoro:

-(■'-«) =0

obliczenie tego wyrażenia nie jest za bardzo pomocne. Tradycyjną metodą określania zmienności jest podniesienie do kwadratu wartości odchylenia od średniej i uśrednienie jej. Wynikająca stąd wartość nazywana jest wariancją próby i oznaczana symbolem V\

V = Hx-/*Y/n

Wariancję próby V często definiuje się jako:

V-2fr-A.)7(n-l)

gdzie (m- 1) oznacza liczbę stopni swobody próby. Ponieważ jednostką wariancji jest jednostka wyjściowa podniesiona do kwadratu, taka jak GBP² lub DEM², co ma niewiele sensu, wyciągamy z V pierwiastek i w ten sposób powracamy do początkowych jednostek. Pierwiastek wariancji to odchylenie standardowe próby. Dla ułatwienia obliczeń wyrażenie opisujące odchylenie standardowe zredukowane jest do postaci:

S = {[2x²-(S^Jx)/«]/(n-l)}^W

Diagram 4.18 ukazuje użyteczne zastosowanie odchylenia standardowego jako miary zmienności próby o n liczbie obserwacji. Kiedy rozkład danych jest normalny, a n jest duże, wówczas zachodzą następujące zależności:

x±S obejmuje około 68 procent danych a±2S obejmuje około 95 procent danych x ± 3S obejmuje około 99 procent danych

Liczba wielokrotności odchylenia standardowego zależy od liczebności próby n lub raczej (n - 1) i liczby stopni swobody próby. Zwiększa się ona u' miarę zmniejszania rozmiaru próby.

Dla wartości n mniejszych od 120 należy odwołać się do tabeli rozkładu t-Studenta, którą odnaleźć można w większości podręczników statystyki.