skrypt wzory i prawa z objasnieniami55

108
Interwał czasoprzestrzenny
■ Ze wzoru = ASj2 cynika, źe wielkość nazywana w mechanice
relatywistycznej interwałem czasoprzestrzennym (lub krótko interwałem) jest niezmiennikiem transformacji Lorentza Oznacza to, ze interwał
czasoprzestrzenny jest taki sam we wszystkich inercjalnych układach odniesienia
■ W mechanice klasycznej, gdzie obowiązują transformacje Galileusza, zarówno czas między dwoma zdarzeniami . jak i odległość przestrzenna między* mmi, są zachowane niezależnie Mówimy ze czas między zdarzeniami i długość są niezmiennikami transformacji Galileusza. (Oczywiście interwał jest również zachowany )
■ Interwał czasoprzestrzenny, którego kwadrat jest większy od zera nazywamy interwałem typu czasowego Jeżeli dwa zdarzenia są oddzielone takim interwałem (np para zdarzeń O i A na rysunku w punkcie 51.1), to zawsze jedno z nich poprzedza drugie (zachowana jest kolejność ich zachodzenia w czasie), niezależnie od wyboru układu inercjalnego, w którym opisujemy te zdarzenia Dla takiego interwału nie istnieje układ inercjalny, w którym zdarzenia mogłyby zajść w tym samym czasie, ale istnieje układ, w którym zdarzenia zajdą w tym samym miejscu Z kolei, jeśli kwadrat interwału czasoprzestrzennego jest mniejszy od zera, to nazywamy go interwałem typu przestrzennego Jeżeli dwa zdarzenia są oddzielone takim interwałem (np para zdarzeń O i C na rysunku), to mc istnieje taki układ inercjalny, w którym zdarzenia te mogłyby zajść w tym samym miejscu, natomiast istnieje taki układ inercjalny, w którym zdarzenia zajdą w tym samym czasie.
■ Współrzędne przestrzenne (x.y,z) i współrzędne czasowe / wszystkich możliwych zdarzeń rozpatrywanych w określonym inercjalnym układzie odniesienia tworzą czterowymiarową przestrzeń zdarzeń o współrzędnych (cł,x,y.z). Tę przestrzeń (czasoprzestrzeń, przestrzeń Minkowskiego) traktuje się jako czterowymiarową przestrzeń "pseudocuklidesową" Termin "pseudo" związany jest z tym, że za odległość między punktami w tej przestrzeni przyjmuje się interwał czasoprzestrzenny, czyli
AS= <J(cAl)2 - (Ax)2 - (Aj')2 - (Az)2 W' przeciwieństwie do przestrzeni euklidesowej, gdzie odległość jest zawsze liczbą rzeczywistą nieujemną, w czasoprzestrzeni odległość może być zarówno liczbą rzeczywistą jak i urojoną
Mechanika relatywistyczna 109
51. Interwał czasoprzestrzenny
układ •-
inercjalny K
pierwsze zdarzenie mające współrzędne (x |.y |. * |) 1 zachodzące w czasie t j
X drugie zdarzenie mające współrzędne
(.t2. i’2-- *) i zachodzące w czasie t2
X
interwał między dwoma* czas między zdarzeniami w układzie K zdarzeniami
v-V-\—
la* czasmiedzs* 1 odległość
odlcgłość przestrzenna międzv zdarzeniami
A/,2 = r2 — /1 A/,2 - ^(Af |2)2^(AVi2)2 + (Ar12)2
interwał w układzie
inercjalnym A
interwał w inercjalnym układzie K' poruszającym się ze stałą prędkością względem układu K
51.1 Czasoprzestrzeń
.V -ct
(ety
fi&n/i - (ct)2 -X2 > o
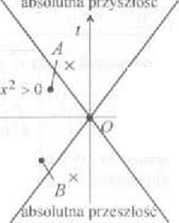
X=Ct
AS
OA
równanie ruchu sygnału rozchodzącego się z prędkością światła w próżni
punkt świata X >
pewnego zdarzenia
x C • absolutne oddalenie *ASq£ (c/)2 x2 < 0
Wyszukiwarka
Podobne podstrony:
skrypt wzory i prawa z objasnieniami17 32 Ruch ciał ze zmienną masą ■ Równanie ( różniczkowe) mchu r
skrypt wzory i prawa z objasnieniami65 128 Entropia ■ Dugą zasadę termodynamiki można sformułować po
skrypt wzory i prawa z objasnieniami49 96 Składanie drgań ■ Przy składaniu drgań o
skrypt wzory i prawa z objasnieniami58 114 Zasady zachowania energii i pędu ■ Musimy pamiętać, że w
skrypt wzory i prawa z objasnieniami35 68Moment bezwładności ■ Należy pamiętać o t
skrypt wzory i prawa z objasnieniami42 82 Równanie drgań harmonicznych ■ W równani
skrypt wzory i prawa z objasnieniami49 96Składanie drgań ■ Przy składaniu drgań o różnych częstościa
skrypt wzory i prawa z objasnieniami58 114 Zasady zachowania energii i pędu ■ Musimy pamiętać, że w
skrypt wzory i prawa z objasnieniami03 4 Układy współrzędnych ■ Układem odniesienia nazywamy ciało,
skrypt wzory i prawa z objasnieniami05 8 Prędkość ■ Tor jest to krzywa opisywana w przestrzeni przez
skrypt wzory i prawa z objasnieniami24 46 Pole grawitacyjne ■ Pole grawitacyjne przy powierzchni Zie
skrypt wzory i prawa z objasnieniami25 Pole sił zachowawczych (potencjalnych) ■ Jeśli w każdym punkc
skrypt wzory i prawa z objasnieniami37 72Moment bezwładności ■ Moment bezwładności
skrypt wzory i prawa z objasnieniami38 74 Ruch obrotowy ciała ■ Jak wynika z własności iloczynu wekt
więcej podobnych podstron