Wyklad4 25252525289 2525252529

10

Aufgabe. Finde anhand des Satzes iiber drei Funktionen (Quetschlemma) folgende Grenzwerte

10

a) lim x³ (4 + sin x)

^b) lim

X-»oo

arctgx ~ V* x + 2

c) limx⁴(2 +sin/-)

X—»oo

d)

lim

X->00

4 + cos)^ x 3x +1

e)

lim

X-»00

2x +Vx 3x + 2

f) lim

x->co

V + sinx y + ar ctgx

g)

lim

x-»oo

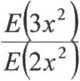
h) limę ^Xsinx

X->0O

Satz:

x->0

lim /(x) = lim /(x₀ + u)

*->*o

lim    f(x) = lim /(-)

x->oo    *->0⁺ U

Aufgabe. Finde folgende Grenzwerte

a)

lim^—-

x^{1 2 3} -1

b)

lim

x—>2

x⁴ -16 x- 2

Grenzwert von ^S—— fiir x -> 0

1

2 2 Cj$/>X sinx<x<

CobX ~    —

Das cosx und

^r Tl ^

x g--;C

V

iiber drei Funktionen gilt

gegen 1 .Gemaft ( zgodnie z ) dem Satz

1

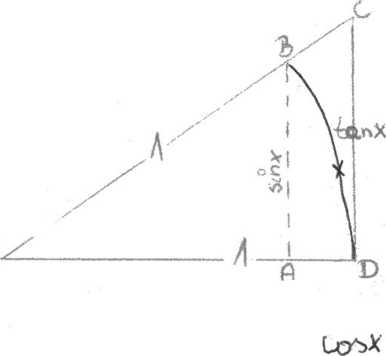
Wir denken uns einen Bogen mit der Lange

x g 0;— J eines Einheitskreises. Die Tangente an den

Bogen wird zum Schnitt mit der Verlangerung des Radius OB in C gebracht. Ein Flachenvergleich zeigt, dass der Inhalt des Kreisausschnittes grófier ais der des Dreiecks OAB und kleiner ais der des Dreiecks ODC ist d.h.

1 1

2

sinx

cosx

2

sinx cosx

- gerade sind, so ist die letzte Ungleichung auch fiir

sinx    KjfrM'

1

--;0 richtig. Fiir x —> 0 strebtJ-

3

   )    cosx