0929DRUK00001715

3

WZORY MATEMATYCZNE ASTRONOM.)I SFERYCZNEJ

cięcia się ich z powierzchnią kuli. Jest zatem «4EAD = .4 EBD = 4.

(Wy więc dwie płaszczyzny, przechodzące przez środek kuli, są do siebie prostopadle, to i określone przez nie dwa wielkie kola są d'o siebie prostopadle; kąty włęffl utworzone w punktach ich przecięcia się, są kątami sferycznymi prostemu Wynika stąd, że wielkie kola, przechodzące przez dany punkt na powierzchni kuli, są prostopadle do głównego kola tego punktu, uważanego za biegun, i odwrotnie, kola wielkie,, prosto

padle. do danego wielkiego koka, przechodzą w Sfc,\ stkie przez bieguny tego wielkiego kola.

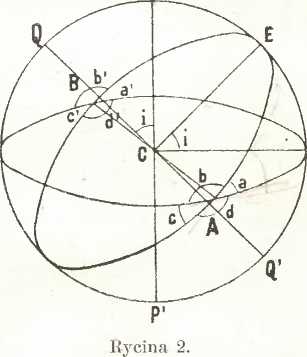
Osi dwóch kół przecinających się nachylone są do siebie pod tym samym katem, co płaszczyzny tych kół, gdyż są do tych ostatnich prostopadle. Wit»c np. na ryc. 2 .4 PCQ = .4 ECD = i. Osi PP i QQ' są oczywiście także prostopadle do prostej AB, a wice. prostopadłą do niej jest, również płaszczyzna PCQ.; płaszczyzna ta określa na |W*ifl&$au kuli wielkie kolo PQJ^yQ', którego biegunami są punkty A i B. To znaczy, że bieguny dwóch przecinających się wzajemnie kół leżą na kole glównem punktów przecięcia się tyoli kól.

Dwa wielkie kola na powierzchni kuli, np. ADB i AEB na ryc.. 2, przecinają się w dwóch punktami A i B, tworząc

l*