0929DRUK00001717

5

WZORY MATEMATYCZNE ASTRONOM,TI SFERYCZNEJ

nowi powierzchnię drugiego trójkąta, mającego te same wierz-cliolki. Boki obu tych trójkątów mają dlugośfe jednakową; co się zaś tyczy kątów, to gdy kąty zaczernionego trójkąta mają wartości a, p i y. to kąty przy tych samych wierzchołkach trójkąta białego mają wartości odpowiedno 360° — a, 360° — [3, 360° — y.

Celem uniknięcia dwuznaczności Co do dwóch możliwych trójkątów, mających wszystkie wierzchołki wspólne, określa się w⁷ trójkącie sferycznym pewien kierunek obiegu jako dodatni, i jako część wewnętrzną trójkąta pizyjmuje się tę, która znaj

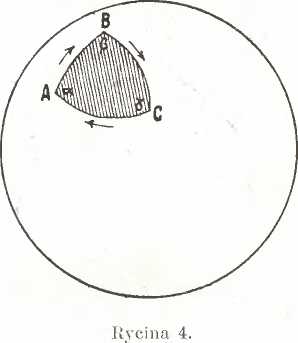
duje się po prawej stronie od dodatniego kierunku obiegu. Kątami wowmęirznemi trójkąta sferycznego są te kąty, które zawarte sa, między wewnętrznemu stronami bokówą a powierzchnią trójkąta jest część pow ierzetoii kuli, ograniczona wewnętrznemi stronami boków.

Jeżoli więc. na rycinie -i w trókącie ABC dodatnim kierunkiem obiegu jest kierunek ABCA, to kąty wewnętrzne trójkąta ABC mają wartość a, [3, y, a powierzchnią jągo jest zaczerniona. część powierzchni kuli. Gdyby zaś kierunek AGBA obiegu byl dodatnim, -to kąty wewnętrzne trójkąta ABD miałyby wartości 360° — a, 360° — (3, 36l)°--y, a powierzchnią jago byłaby biała część powierzchni kuli.