0929DRUK00001731

19

WZORY MATEMATYCZNE ASTRONOM.JI SFERYCZNEJ

Łącząc wierzchołki A; B, C lukami w Luj ki cli kól z 'Wierzchołkami X, Y, Z, otrzymujemy 9 następujących trójkątów sferycznych, mających jako wspólny wierzchołek punkt K:

XAK, YAK, ZAK, XBK, Y BK, ZBK, XOK, YGK, Z GIC, ^

z których w spoźólą nie 'wymagający wyjaśnienia, wynikają następujące wartości dostaw kątów tabelki:

(Sas-łJ/ cos / + sin 4 sin % Cos¹/,

-    sin Ą cos x + <-oS 4 Sin / cos */,

-    Sin y_ sin i,

-    cos | Sin y. + sto >b cos x cos i, ' sin <b sin x -f- CoS ó Cos % cqs i,

-    oos x sin i. sin 4 rsin i, cos ę sin i, cos i.

j cos a_t (“os oą hos a₃ cos Pj

oo$ [ST;

cos p_s oosy, oosy₂ cosy₃

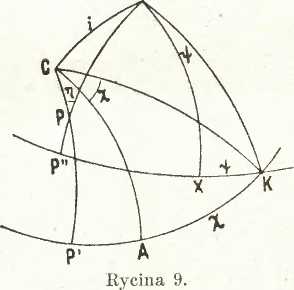
W istocie więc 3 wielkości <b, x, i w zupełnośtei określają położenie trójkąta XYZ w zględem trójkąta ABC i odwrotnie. Oczywiście przez te same trzy wielkości określone być może wzajemne-położenie dwtł-h układów sferycznych GAB i ZXY, stosownie do przyjętego oznaczenia (ust. 4).

6. Zmiana spółrzędnych sferycznych. Niechaj p i § i ry<V 9) będą spólrzędnemi sferyezuemi punktu P w układzie jCAB-

2*