0929DRUK00001787

75

WZORY MATEMATYCZNE ASTRONOMJI SFERYCZNEJ

Zastosujmy najprzód wzó 17*47,* W tym przykładzie jest

/-(a) = 25° 56' 7."Oj A f{a) = 0ⁿ 38' 52."8, A² f\a) - — 18' 24.' 6, A³ f{a) = — 0' 15."7, A- f (a) — -f- 17." 8, A⁵ f(a) = + 0."1.

Spólćzynniki wzoru (47) dla m = 0.68 mają wartości następuj ąttel''

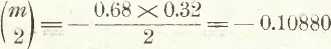
0.68 x0.32 X 1.32 6

- = 0.0470

0.68 X 0.42 X 1.32x2,82

24

— 0.0278

Utrzymujemy wiec

/'(«) = 25°. 56' 7."0 m A f\a) = -f- 26' 26." 3

— 0." 7

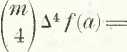
0." 4

8 (0.34) = 26° 24' 32".4

Zastosow anie wzoru N e w t o n a ułatwia tablica II (na końcu książki), zawierająca wartości-iSpólizynników poszczególnych wyrazów- wzoru dla różnych wartości m.

Celfem zastosowania wzoru (47') mamy w naszym przykładzie

A²/'(n    h)=    17' 51." 9,    Ami#_:— /?) = — 0"32 " 7

AV(a — 2A) = +    15." 7,    A⁵/'(«*- 2h) = -f-    l."3;