0929DRUK00001779

67

WZORY. MATEMATYCZNE ASTRONOMJI SFERYCZNEJ

Wzorowi (47) można nadać np. taką postać, ażeby występowały w nim te różnice rzędu parzystego, które stoją, w tym samym wierszu, co /(<*); t. j. A² fia— 7?)£ A⁴/¹ (a — 27?), A^K f(a—    ... "Do utworzenia tjBćk różnij potrzebne Są od

powiednio po I, 2, +... wartości funkcji f (cc)¹- dla argumentów mniejszy cii i większyoh niż a Różnice!, rzędu nieparzystego można obrać dowolnie, Ł j. albo fce, które stoją >v tym wierszu, co A f(a — h)_y lub też w tym wierszu, go A f{a). Gdy mają we ■wzorze występować różnice wiersza niższego niż f{a), jest wówczas:

A² f(a) = A² fia k)    + A⁸ fia — fi),

A^:! /‘(«) = A* f{a — h)    + A⁴ f(a — 27?) -f    A⁵ f(a — 27?),

A ¹ j ą.) - A⁴ fia — 7?)    + A* pa — h) =

= a¹ fia — 27?) + 2A⁵ f(a - 27?) -f    A^fi f{a — 37?) + A⁷ fia—37?)

i t. d.

Podstawiając we wzorze (47) powyższe, wartości, znajdujemy:

f(a + mfi) = f{*) + j lf(a) -f - Ą p-^} A² fia - 7?) +

+

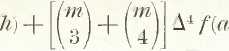
27?j +

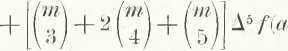
27?) +

i po łatwych redukcjach

ffi + mii) = f ,ti + j)j A />>+ W A f{a — AJ-f-

+ (") A- fia - ti + (’") = + A- fia - 2,„ +

+("') ^(w+1lf ^{+ g}-⁾ * m    + • ■ ■ ■    +

Gdy zaś we w zorze interpolacyjnym występować mają m/mice nieparzystego rzędu, które Stoją'w wierszu wjższym, niż fia), jest wtedy:

5*