0929DRUK00001759

WZORY MATEMATYCZNE ASTRONOMJI SFERYCZNEJ 47

więc

----sin 2y

(m — fjsin 2 y _ m + 1    “ ¹

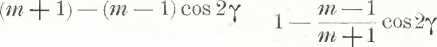
tang (y' — yj

Stopując zatem trzeci ze wzorów (56"), otrzymamy

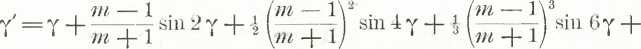
Przykład rachunku z pomocą powyższego wzoru znajduje się niżej w ustępie 25.

12. Wzór j/ = }1    -)-??> cosr,.

Do tej postaci sprowadzają się wyrażenia

q = i 11\-p² ± 2p cos r„

(o)

ą = y 1 p² ± 2-p sin r_h

gdy j> > U. Jest mianowicie:

gdy y = 180° — -o, ]/1 —+ 2<je cos (180°— r,) = |'l -\-p>² —2p cos r_t, gd) y = 90° — Yj, y 1 -f-p'" +    c°S (90° — J) = /l +jo²-(-2y) sin rj

gdy y = 90° + r„ yi -j-p²    2p cos (90° + vj) jg= |rl Ą-p²— 2p sin bp

Z drugie;, strony </ mii tutaj to samo znaczenie, co we wzorach (mi, a więc -wzór (2(5) jest, rozwinięciem logu q według dostaw wielokrotności kąta y. (i dyby 'chodziło o rozwinięcie lo-gaiytmu zayklego, t. j. log#, to należy jeszcze tylko poszczególne wyrazp szeregu (jł6) pomnożyć przez moduł zwykłych lo-garytmów M. Jak wiadomo, jest

M = 0.434294481903261 . . .