0929DRUK00001763

WZORY MATEMATYCZNE ASTRONOMJJ SFERYCZNEJ ,51

Ponieważ dla tej nowej zmiennej granice całkowania są te same, co dla zmiennej y, więc jest

00 00

k² = JdM./asfe~⁽¹ + “²⁾*'² dar.

O    O

Wartość drugiej z całek powyższego wyrażenia znajdujemy z łatwością. Ponieważ

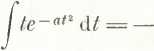
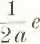
at-

_J_.

1 -f u ² ’

więC °°

/ajfind-H <W d ar =

podstawiając tę- wartość w wyrażeniu na /.², znajdziemy

k²

1 f d u

§h f «-

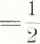
arct&ng u

11> 4'

O

Jest zatem

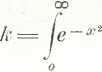
<** = o P

(31)

oraz

00

»1')

!ik= Je~^x2 rLr = p^/rc.

— OO

00

<? ®³ fe ~ dar = 4 (a).

a

W specjalnym przypadku, gdy « = 0, całka powyższa sproć wadza się do wzoru (31), t. j. w*UU- r /tt. W przypadku ogólnym wartość funkcji ^(a) otrzymuje się z szeregów, którym można nadawać rozmaitą postać. Rozwijając naprzykład na szereg' potęgowy funkcję e~^x% otrzymujemy

/y» 2    /y> 4:    /y» 6

I    *

' jT + SF jTT^- ’

4*