FizykaII264�01
258
258

Fig. 119.
rur A i B (Fig 119), z których jedna wsuwać się daje w drugą. Rurka A ma w śmduu denka mały' otwór, a rurka B jest na lewym końcu n zamknięta mato-wem szkłem, albo prześwietlającym papierem. Obróciwszy tę podwójną rurę otworem do oświeconego przedmiotu i rozsunąwszy ją należycie, widać jego obraz rzucony na zasłonę przy n.
3) Ubywanie mocy oświetlenia z oddaleniem od źródła światła. Ponieważ promienie światła rozchodzą się z punktu świecącego w liniach prostych, więc oświetlenie pewnej powierzchni ciała ciemnego musi być- słabsze, jeśli oddalenie jej od źródła światła jest znaczniejsze. Dla wykazania prawa, według którego moc oświetlenia danej powierzchni pomniejsza się z odległością od źródła światła, pomyślmy sobie punkt świecący najprzód w środku wydrążonej próżnej kuli, mającej promień wydrążenia r, a następnie znowu w środku większej kuli, mającej promień’ wydrążenia R. Promienie światła padają tak w pierwszym, jak w drugim razie na wewnętrzną powierzchnię kulistą wszędzie pod tym samym kątem (prostym), muszą więc w każdym jej punkcie trafionym sprawiać jednakowe oświetlenie, czy ona bliżej tego punktu środkowego leży, czy jest bardziej od niego oddalona. Atoli, jakakolwiek jest natura światła, rzeczone dwie powierzchnie muszą się różnić od siebie oświetleniem, gdyż w obu razach równa ilość światła rozpościera się na nierównych powierzchniach. A że kuliste powierzchnie tak się mają do siebie, jak drugie potęgi ich nromieni, będących tu odległościami od punktu świecącego, więc oznaczywszy głoską e oświetlenie wnętrza kuli R, a głoską E oświetlenie wnętrza kuli r, mają się te oświetlenia widocznie do siebie odwrotnie, jak wielkości oświeconych powierzchni, t. j.
E\e — 4r2n : 4R2n — r2: A2,
czyli moc oświetlenia na różnych, do koła świecącego punktu zatoczonych, kulistych powierzchniach jest w odwrotnym stosunku do Kwadratów z ich odległości od tegoż punktu. Jeś’i e jest moc oświecenia jednostki powierzchni na kuli, mającej promień r = 1, E zaś na kulistej powierzchni promienia R, będzie
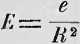
Wyszukiwarka
Podobne podstrony:
FizykaII360�01 356 356 Fig. 105. przezroczystego w drogiej rozsypuje się na pewne części składowe, k
FizykaII098�01 93 93 Fig. 47. popychania i dośrodkowego cofania się. Powiększenie bowiem objętości k
FizykaII132�01 127 127 Fig. 55. ce się nawzajem, nadać krążkowi ss ruch obrotowy, którego chyżość&nb
FizykaII615�01 tóll przy a, b {Fig. 342) i przy f e, tudzież w samym środku łącznika przy c, d, aby
FizykaII814�01 808 808 Fig. 449. su umieszczonych, jak to rysunek (Fig. 449) przedstawia. Gdy się do
FizykaII273�01 267 267 ■ Fig. 124. urządza się po-działkę na rynience przyrządu w ten sposób, iż&nbs
FizykaII054�01 49 49 Fig. 19. z razu tak w kierunku rzędnych //, jako też i odciętych z do miejsca&n
FizykaII172�01 166 166 Fig. 75. nie odwrotnie, t. j. nie każdemu innemu podziałowi blachy odpowiada
FizykaII175�01 169 169 Fig. 77. Fizyka IV TI. Wszystkie części, służące do zadęcia, są tu stale osa
FizykaII193�01 187 187 Fig. 85. Fig. 86. ku, naeiągniętemi na stosowną rurkę, lecz próby te nie
FizykaII236�01 230 230 Fig. 99. razem z jej dołem, przez CFD przesłanym, drgający ruch cząstek powie
FizykaII243�01 237 237 Fig. 10Ł równocześnie widełki strojowe, zupełnie jednozgodne z tonem niższym
FizykaII253�01 247 < 247 < Fig. 110. Dzieje się to przez nawoskowanie jćj w tem pierwej poczer
FizykaII261�01 255 255 Fig. 116. na od przestrzeni ośw:econej. Ztąd to pochodzi, iż koniec c;enia wy
FizykaII291�01 285 285 Fig. 137. ło się Figdko około piono-0SF a następnie po od-J?V. biciu się od
FizykaII293�01 287. 287. : Fig. 138. i w punkcie li występuje z niej w kierunku By, podczas gdy inna
FizykaII309�01 303 303 Fig. 144. go na prawo i odwrotnie. Drzewa lub inne przedmioty na brzegu więks
FizykaII337�01 331 331 Fig. 171. całkiem się odbijają,. Nalewając wody do rurki, znika to zjawisko&n
FizykaII363�01 859 859 Fig, 199. skupiające wszystkie promienie w ognisku sprzężonem na małej,
więcej podobnych podstron