0463

465

§ 6. Szeregi oscylujące i szeregi asymptotyczne — Wzory Eulera-Maclaurina

Jeżeli utożsamimy B (x) z A (x), to otrzymamy rozwinięcie kwadratu [A (x)]^a. Analogicznie możemy otrzymać rozwinięcie asymptotyczne funkcji [A (x)]", gdzie m jest dowolną liczbą naturalną.

3° Niech teraz dana będzie pewna funkcja F(y) analityczna w punkcie y — 0, tzn. funkcja, którą można w otoczeniu tego punktu rozwinąć w szereg potęgowy

F(y) = £ fimf-Po+hy+P* y²+ ... +Pmy”+ ...

K~0

Rozpatrzmy poza tym funkcję A (x), która ma rozwinięcie asymptotyczne bez wyrazu wolnego: (12)    +    ... +-2j|-+ ....

XX¹    *"

a więc A (x) -*■ 0, gdy x -*■ oo. W tym przypadku ma sens funkcja złożona

F(A(x)) = J/U A(x)r,

przynajmniej dla dostatecznie dużych x.

Funkcja F(A (x)) ma rozwinięcie asymptotyczne, które możemy otrzymać z poprzedniego rozwinięcia» gdy zamiast każdej z potęg [A (x)]" podstawimy jej rozwinięcie asymptotyczne i dokonamy w sposób formalny redukcji wyrazów podobnych [porównaj 446].

Zauważmy przede wszystkim, że w otoczeniu punktu y — 0 funkcja F(y) ma ciągłą (a więc również ograniczoną) pochodną i dla dowolnych dwóch punktów y i y tego otoczenia jest spełniona nierówność

\F(y)~F(y)\ < L-\y-y\    (Z. = const) .

Oznaczmy n-tą sumę częściową szeregu (12) przez A„(x):

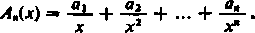
Przy ustalonym n obie funkcje A (x) i A,(x) trafią dla dostatecznie dużych x do wspomnianego otoczenia a więc

|*"[F(/1 (*))-F/f„(*))]| < Lx"\A (x)-/(_n(x)| = Lx*\r„(x)\ -* 0 ,

gdy x -* oo, i

F(A (x)) = F(A„(x))+o    .

Z drugiej strony, na podstawie znanego już nam twierdzenia z ustępu 446, mamy dla dostatecznie dużych x

F(A„(x), = p₀+ f; UA„ (x))^m - iL£L + h    l + Pi °* + ²feg    ₊...

*1-1 ^

i z uwagi na poprzednią zależność możemy taką samą równość napisać dla F(A (x)), co dowodzi prawdziwości rozwinięcia asymptotycznego

F(A (x)) ~ Po-i-    ^ai~^~Pi ^ai ą. Pi ^fl3~t~2^2 fli gą-*-/?3 ai _j_ ^^ _|_ Pi n»+ ... +M ^

⁰ X    X²    X^ł    X*

o które chodziło.