84606 str266

266 5. ZARYS RACHUNKU TENSOROWEGO

Niech w W-wymiarowej przestrzeni Euklidesa będą dane dwa układy współrzędnych krzywoliniowych. Przez X¹, x², ...,x^N oznaczamy współrzędne pewnego punktu tej przestrzeni w układzie pierwszym, natomiast przez jc'¹, x'², x'^N — współrzędne tego punktu w układzie drugim. Przyjmujemy, źe wymienione współrzędne są ze sobą związane zależnościami

266 5. ZARYS RACHUNKU TENSOROWEGO

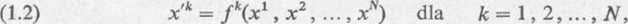
gdzie/* są danymi funkcjami mającymi ciągłe pochodne do rzędu drugiego włącznie, przy czym jakobian

d*'¹ Jx'¹ dxⁿ

dx^l    dx²    dx^N

(1.3)

8x'^N dx'^N dx’^N

dx^l dx² dx^N

Założenia dotyczące funkcji f^k mogą dotyczyć całej przestrzeni lub też pewnego obszaru ograniczonego O.

Uwaga. Kolejne współrzędne punktu będziemy oznaczali górnym wskaźnikiem, jak to zostało już wyżej uczynione.

Dla uproszczenia pisowni wprowadzimy obecnie następujące założenia dotyczące zapisu:

1. Umowa dotycząca rzędu. Jeżeli w jakimś wyrażeniu występuje jednokrotnie wskaźnik (górny lub dolny) napisany małą literą alfabetu łacińskiego, to będziemy rozumieli, że przyjmuje on wszystkie wartości 1,2, gdzie N jest liczbą wymiarów przestrzeni, np.

a' dla N = 5 oznacza {a¹, a², a³, a*, a⁵},

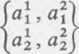
t

a^k dla N = 2 oznacza    ,

b_mdla N = 3 oznacza

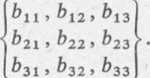
2. Umowa sumacyjna. Jeżeli w jakimś wyrażeniu dwukrotnie występuje wskaźnik pisany tą samą literą alfabetu łacińskiego, to będziemy rozumieli, że w wyrażeniu tym występuje sumowanie względem tego wskaźnika, przy czym przyjmuje on wartość 1,2, ..., N. Na przykład różniczka zmiennej określonej zależnością (1.2) wynosi

AT

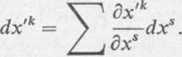
(1.4)

5= 1

Zgodnie z umową sumacyjną możemy tę różniczkę zapisać w postaci

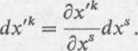
(1.5)

Wyraźnie jest tu widoczna ekonomia zapisu wzoru (1.4).