23 luty 07 (50)

Podczas ruchu mechanizmu suwak 4 pozostaje stale w płaszczyźnie Oxy, a zatem jego ruch względem układu nieruchomego jest ruchem płaskim. Ten ruch płaski suwaka można traktować jako ruch złożony z ruchu unoszenia prowadnicy 2 i ruchu względnego suwaka 4 względem prowadnicy 2. Obserwując ruch suwaka 4 w ruchomym wykonującym ruch płaski układzie współrzędnych 0,^/j widzimy, że przemieszcza się on po krzywoliniowej prowadnicy 2. Torem środka suwaka (w tym przypadku punktu D) w ruchu względnym jest krzywa BC.

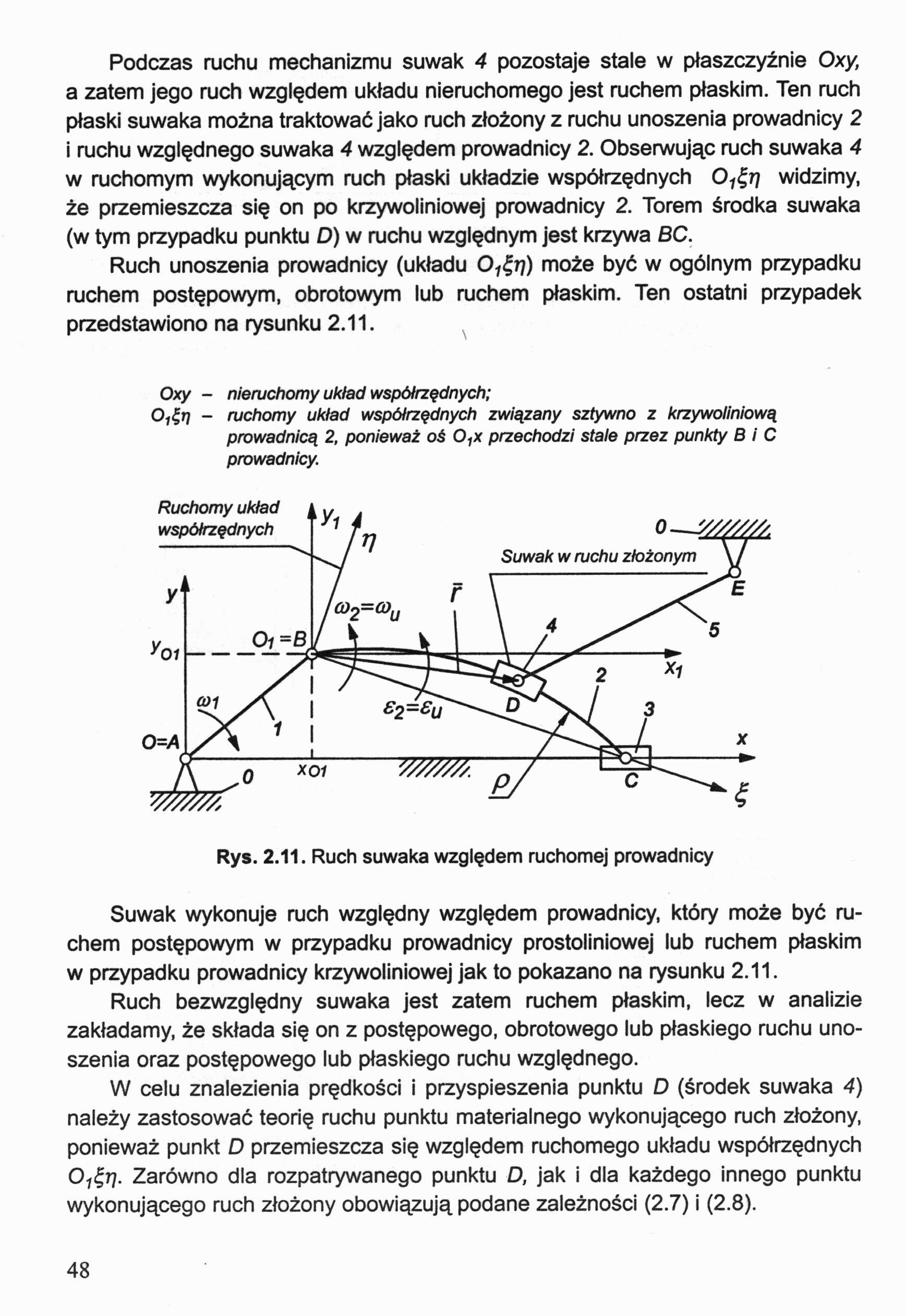
Ruch unoszenia prowadnicy (układu O^rj) może być w ogólnym przypadku ruchem postępowym, obrotowym lub ruchem płaskim. Ten ostatni przypadek przedstawiono na rysunku 2.11.

Oxy - nieruchomy ukiad współrzędnych;

O^r) - ruchomy układ współrzędnych związany sztywno z krzywoliniową prowadnicą 2, ponieważ oś 0,x przechodzi stale przez punkty B i C prowadnicy.

Rys. 2.11. Ruch suwaka względem ruchomej prowadnicy

Suwak wykonuje ruch względny względem prowadnicy, który może być ruchem postępowym w przypadku prowadnicy prostoliniowej lub ruchem płaskim w przypadku prowadnicy krzywoliniowej jak to pokazano na rysunku 2.11.

Ruch bezwzględny suwaka jest zatem ruchem płaskim, lecz w analizie zakładamy, że składa się on z postępowego, obrotowego lub płaskiego ruchu unoszenia oraz postępowego lub płaskiego ruchu względnego.

W celu znalezienia prędkości i przyspieszenia punktu D (środek suwaka 4) należy zastosować teorię ruchu punktu materialnego wykonującego ruch złożony, ponieważ punkt D przemieszcza się względem ruchomego układu współrzędnych O^rj. Zarówno dla rozpatrywanego punktu D, jak i dla każdego innego punktu wykonującego ruch złożony obowiązują podane zależności (2.7) i (2.8).

48