24 luty 07 (22)

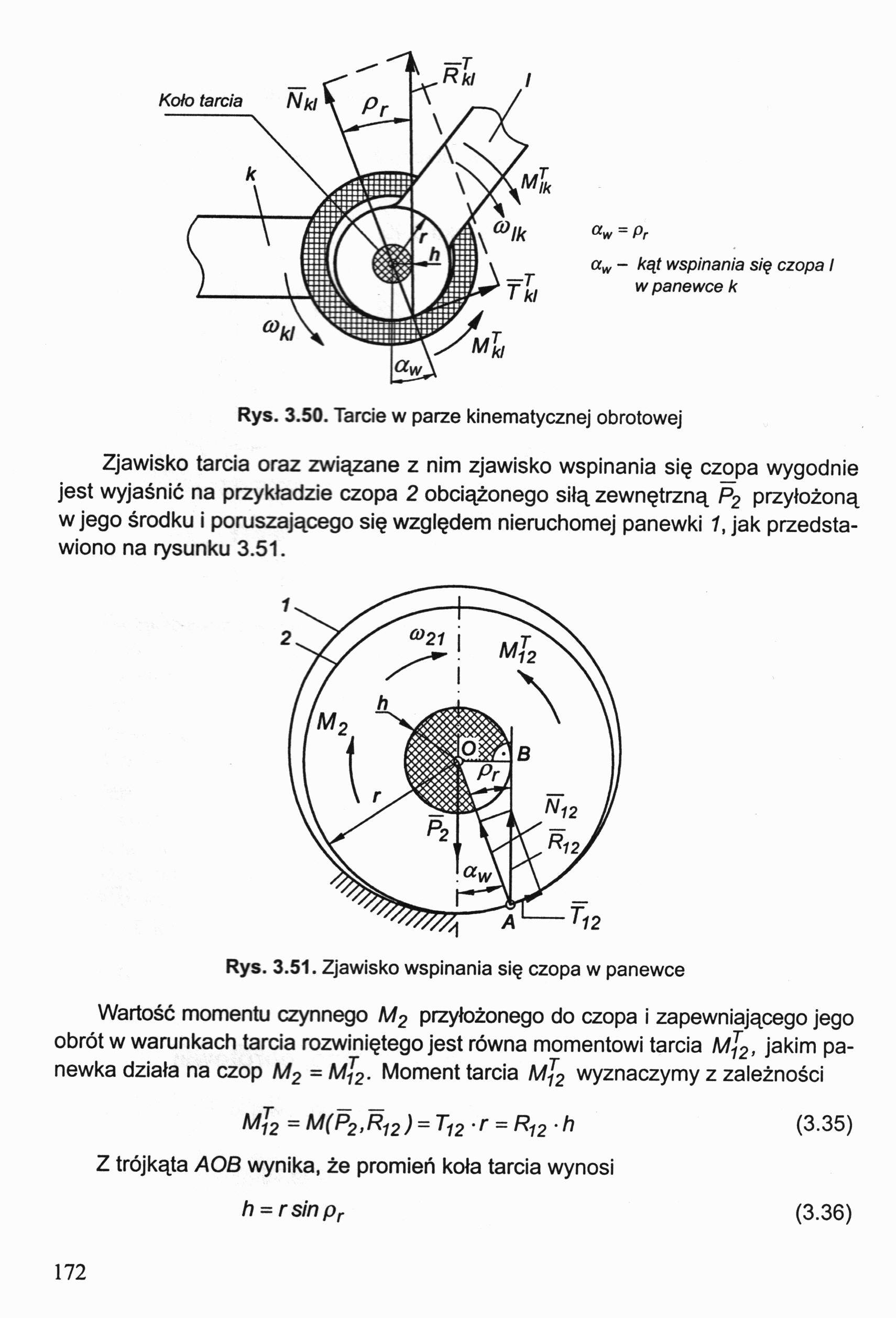
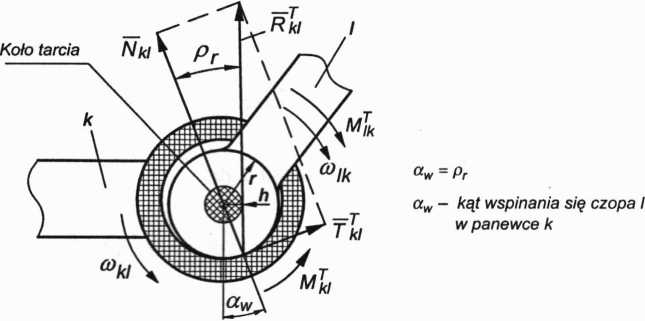
Rys. 3.50. Tarcie w parze kinematycznej obrotowej

Zjawisko tarcia oraz związane z nim zjawisko wspinania się czopa wygodnie jest wyjaśnić na przykładzie czopa 2 obciążonego siłą zewnętrzną P₂ przyłożoną w jego środku i poruszającego się względem nieruchomej panewki 1, jak przedstawiono na rysunku 3.51.

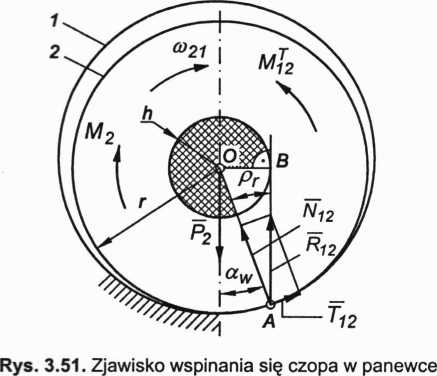
Wartość momentu czynnego M₂ przyłożonego do czopa i zapewniającego jego obrót w warunkach tarcia rozwiniętego jest równa momentowi tarcia mJ₂, jakim panewka działa na czop M₂ = mJ₂. Moment tarcia mJ₂ wyznaczymy z zależności

mJ₂ = M(P₂,R₁₂ ) = T₁₂ r = R₁₂ h    (3.35)

Z trójkąta AOB wynika, że promień koła tarcia wynosi

h = rsinp_r    (3.36)

172