24 luty 07 (54)

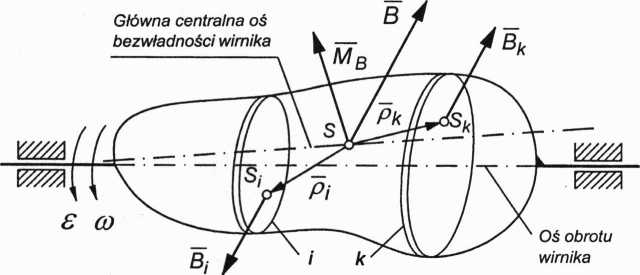
Rys. 3.74. Model fizyczny niewyrównoważonego wirnika w postaci cienkich niewyrównoważonych tarcz prostopadłych do osi obrotu

W wyniku redukcji otrzymujemy wektor główny sił bezwładności B oraz moment główny sił bezwładności M_B przyłożone w środku masy wirnika S:

B =

i=1

(3.72)

M_B = lP_ixB_i i=1

Wektor główny sił bezwładności B jest prostopadły do osi wirnika i przechodzi przez jego środek masy S. Moment główny sił bezwładności M_B jest prostopadły do głównej centralnej osi bezwładności obrotu wirnika i przechodzi przez jego środek masy S. Ponieważ wirnik jest niewyrównoważony dynamicznie, oś obrotu wirnika oraz główna centralna oś bezwładności wirnika są prostymi skośnymi. Przyjmujemy dwie dowolne płaszczyzny n₁ i n₂ prostopadłe do osi wirnika, w których przyłożymy dwie siły i B₂ bezwładności w taki sposób, aby nowy układ sił był statycznie równoważny zadanemu układowi B i M_B, co przedstawiono na rysunku 3.75.

W celu ustalenia kierunków i wartości sił ty i B₂ przeprowadzimy następujące kroki:

1.    wektor główny B rozkładamy na dwie siły równoległe działające w płaszczyznach 7i-j i TT2 takie, że B = B'f +B'₂\

2.    moment główny M_B przedstawiamy w postaci pary sił B"? oraz B"₂ takiej, że: M_b = M_b(b"i , B"₂)= pxB"₂.

204