24 luty 07 (115)

Przykład 3.34

Masy i siły działające na człony maszyny zredukowano do członu napędzającego (rys. 3.117a). Zredukowane momenty sił czynnych M_c(qj) oraz biernych M_b(cp) zmieniają się jak na rysunku 3.117b. Wartość zredukowanego momentu bezwładności jest stała i wynosi J_zr =0,1 kgm². Warunki początkowe: dla t = 0, (p(0) = 0, <p(0) = 0. Obliczyć prędkość kątową członu napędzającego mechanizmu po wykonaniu przez niego trzech pierwszych obrotów <p_k = 6n.

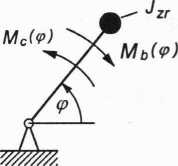
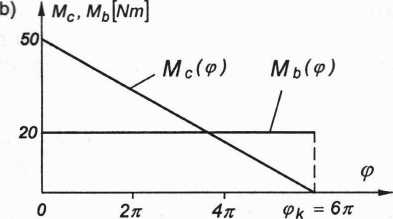
Rys. 3.117. Model członu redukcji: a) model dynamiczny mechanizmu; b) charakterystyki momentów czynnego M_c i biernego M_b zredukowanych do członu napędzającego

Rozwiązanie

Korzystając z równania (3.128) mamy

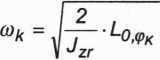
(P3.248)

gdzie zgodnie z rysunkiem 3.117b:

^~0,ę_K ~ Lc ~ l-b

6k    j

(P3.249)

L_c = \M_c(ę)dcp = -50-6n = 150n N-m o    ²

6n

^Lb = \M_b(ę)d(p = 20-6n = 120n N-m    (P3.250)

0

Ostatecznie prędkość kątowa członu redukcji po trzech pierwszych obrotach od momentu uruchomienia wyniesie

co_k=_]l~j^=⁴³,⁴² s"¹    (P3.251)

265