24 luty 07 (49)

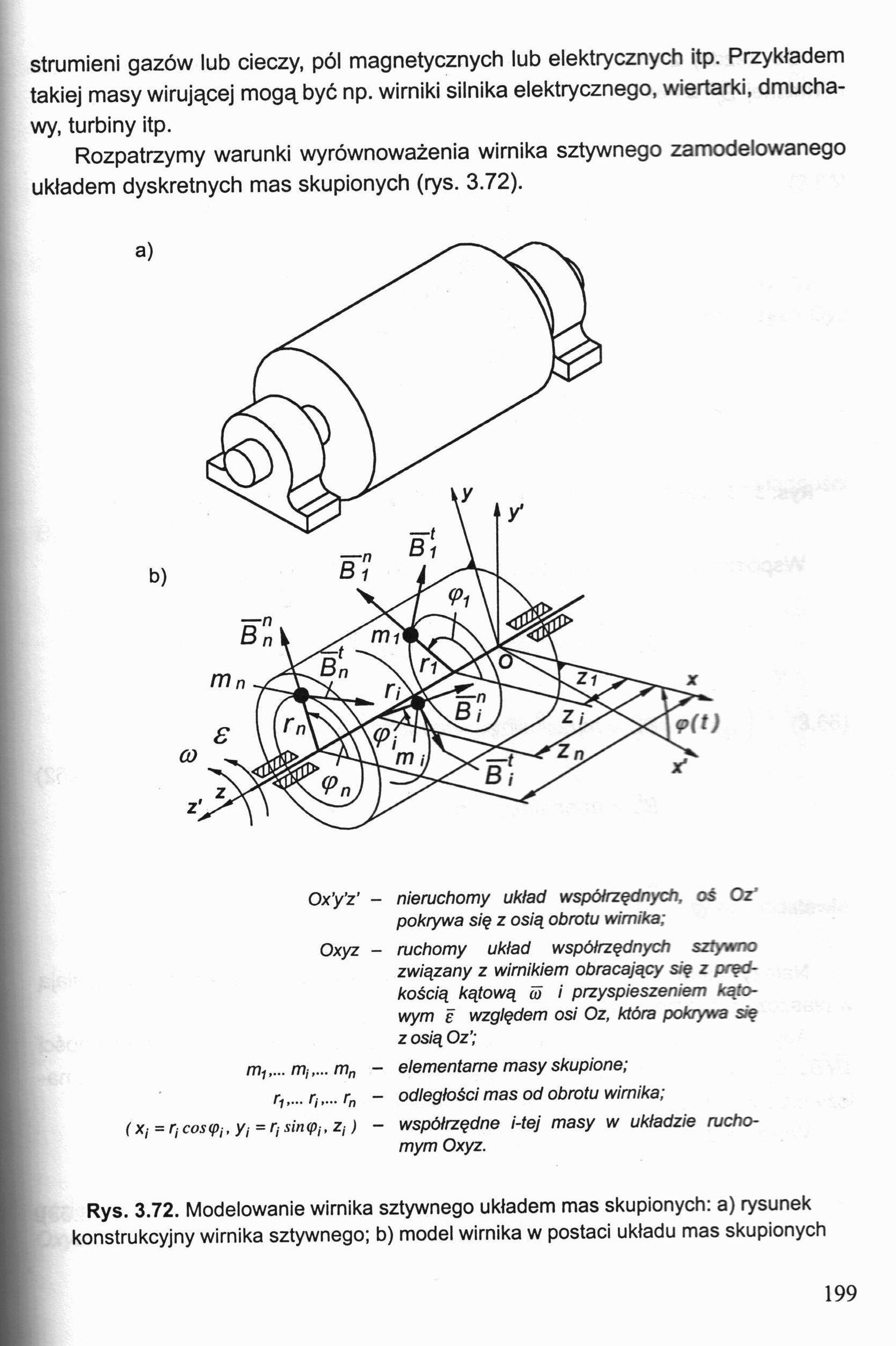
strumieni gazów lub cieczy, pól magnetycznych lub elektrycznych itp. Przykładem takiej masy wirującej mogą być np. wirniki silnika elektrycznego, wiertarki, dmuchawy, turbiny itp.

Rozpatrzymy warunki wyrównoważenia wirnika sztywnego zamodelowanego układem dyskretnych mas skupionych (rys. 3.72).

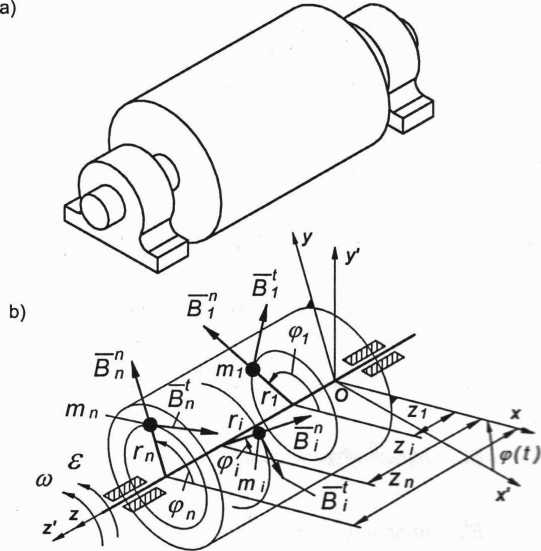
Ox’y’z' - nieruchomy układ współrzędnych, oś Ot pokrywa się z osią obrotu wirnika;

Oxyz - ruchomy układ współrzędnych sztywno związany z wirnikiem obracający się z prędkością kątową cii i przyspieszeniem kątowym ś względem osi Oz, która pokrywa się z osią Oz’;

m,,... mi,... m„ />,... r„... r_n (xi = rj cosipj, yi = r, siny,, z,)

elementarne masy skupione; odległości mas od obrotu wirnika; współrzędne i-tej masy w układzie ruchomym Oxyz.

Rys. 3.72. Modelowanie wirnika sztywnego układem mas skupionych: a) rysunek konstrukcyjny wirnika sztywnego; b) model wirnika w postaci układu mas skupionych

199