24 luty 07 (95)

Uwaga. Równania (3.118) lub (3.119) nazywamy równaniami ruchu członu redukcji w postaci energetycznej.

Na podstawie (3.119) możemy obliczyć prędkość kątową członu redukcji w położeniu „/”

U); =

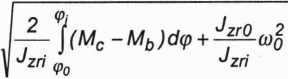
(3.120)

Jeśli prędkość początkowa (o₀ = 0 (zachodzi rozruch układu), to

(Oj =

J-^Vf(M_c-M_b)dę

V ^zri <Po

(3.121)

Wychodząc z zasady równowartości energii kinetycznej i pracy w postaci całkowej, mamy:

Ej-E₀=L_0i, i = 1,2,..., n

(3.122)

gdzie:

Ej - energia kinetyczna członu redukcji w położeniu , i ”,

E₀ - energia kinetyczna członu redukcji w położeniu początkowym „0”,

L_0i - praca wszystkich sił działających na mechanizm przy przejściu z położenia „0” do położenia „ / ”,

stąd

^Ei =^Eo ^+L0i

(3.123)

Jednocześnie energia kinetyczna członu redukcji w położeniu wyraża się wzorem:

1    2    1    2

^Ei =^zn^i lub Ej = —m_zrjVj

(3.124)

stąd:

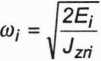
lub

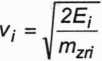
(3.125)

245