24 luty 07 (118)

ę_c - kąt obrotu członu napędzającego odpowiadający cyklowi kinematycz nemu,

k - liczba cykli kinematycznych w okresie rozruchu,

n - liczba kroków obliczeń numerycznych,

k • (o

Aę = —— - stały krok obliczeń n

<Pi+1 =<Pi + A<P,

^Mzri = M_zr(<P_i,<n,,t_i) = M_zrci-M_zrbi, Jzri ~ ^zr (Vi )i    Jzr(i +1) ~ Jzr (<Pi+1 )>

_M_zriAtp , 3J_zri-J_Zr(i₊i)

JzntOj    2J_zrl

®i+1 ~    ,    ⁺    oi    ^/»

co_iri=^P-,

^ei+1--T~ ®śri>

A(p

Wykresy: aję,); lub coM); e,fU

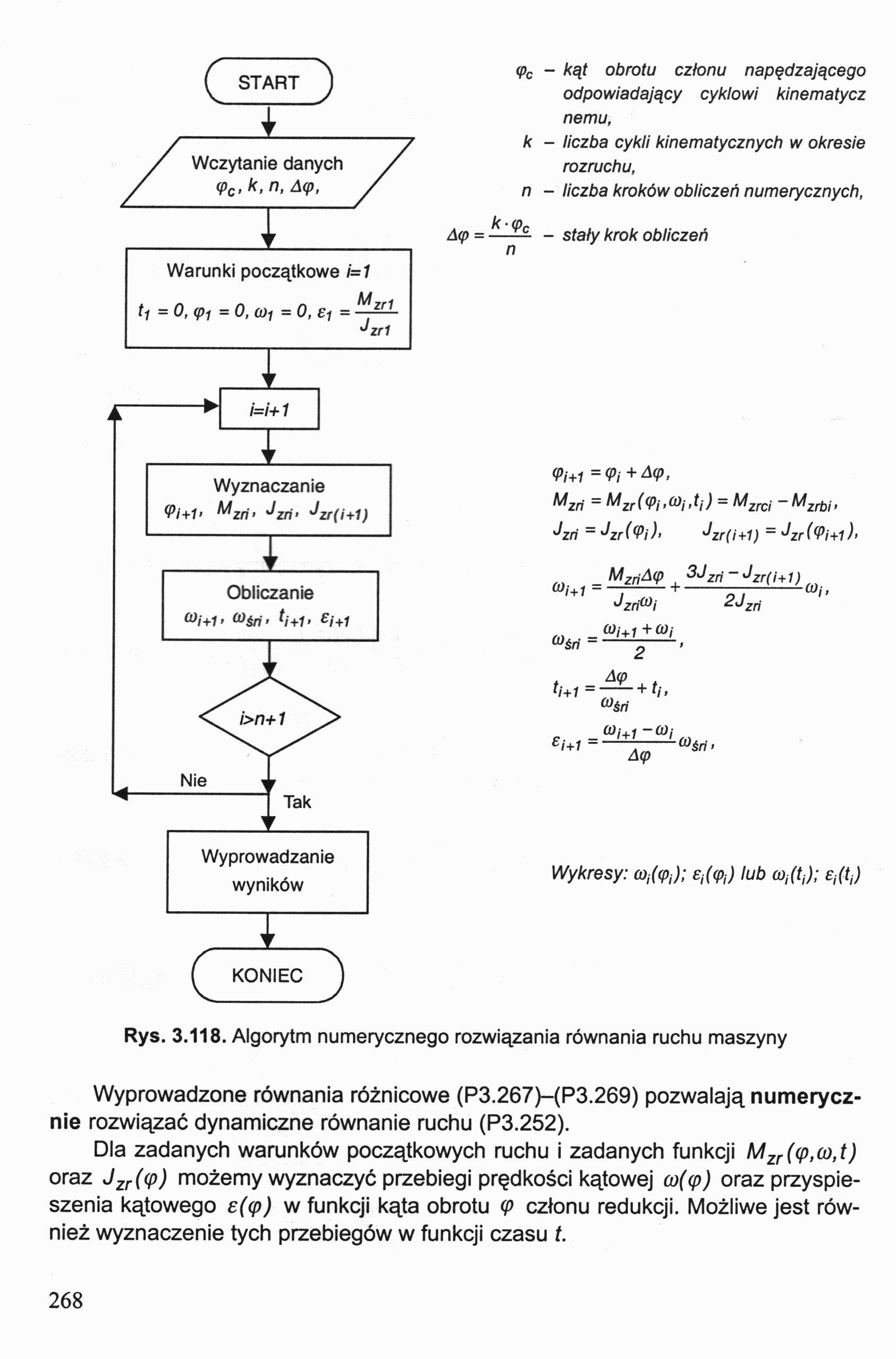
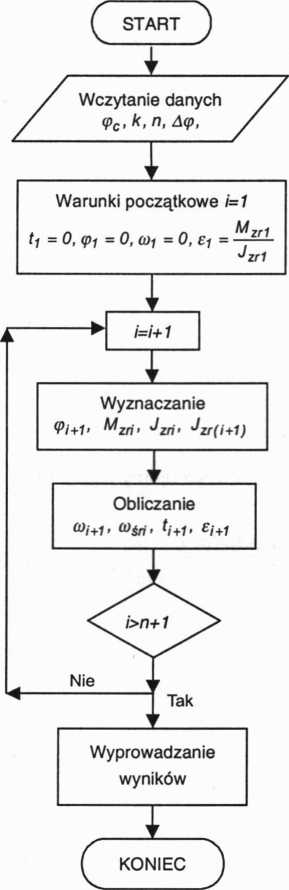
Rys. 3.118. Algorytm numerycznego rozwiązania równania ruchu maszyny

Wyprowadzone równania różnicowe (P3.267)-(P3.269) pozwalają numerycznie rozwiązać dynamiczne równanie ruchu (P3.252).

Dla zadanych warunków początkowych ruchu i zadanych funkcji M_zr((p,co,t) oraz J_zr(cp) możemy wyznaczyć przebiegi prędkości kątowej co(ę) oraz przyspieszenia kątowego e((p) w funkcji kąta obrotu (p członu redukcji. Możliwe jest również wyznaczenie tych przebiegów w funkcji czasu f.

268