24 luty 07 (86)

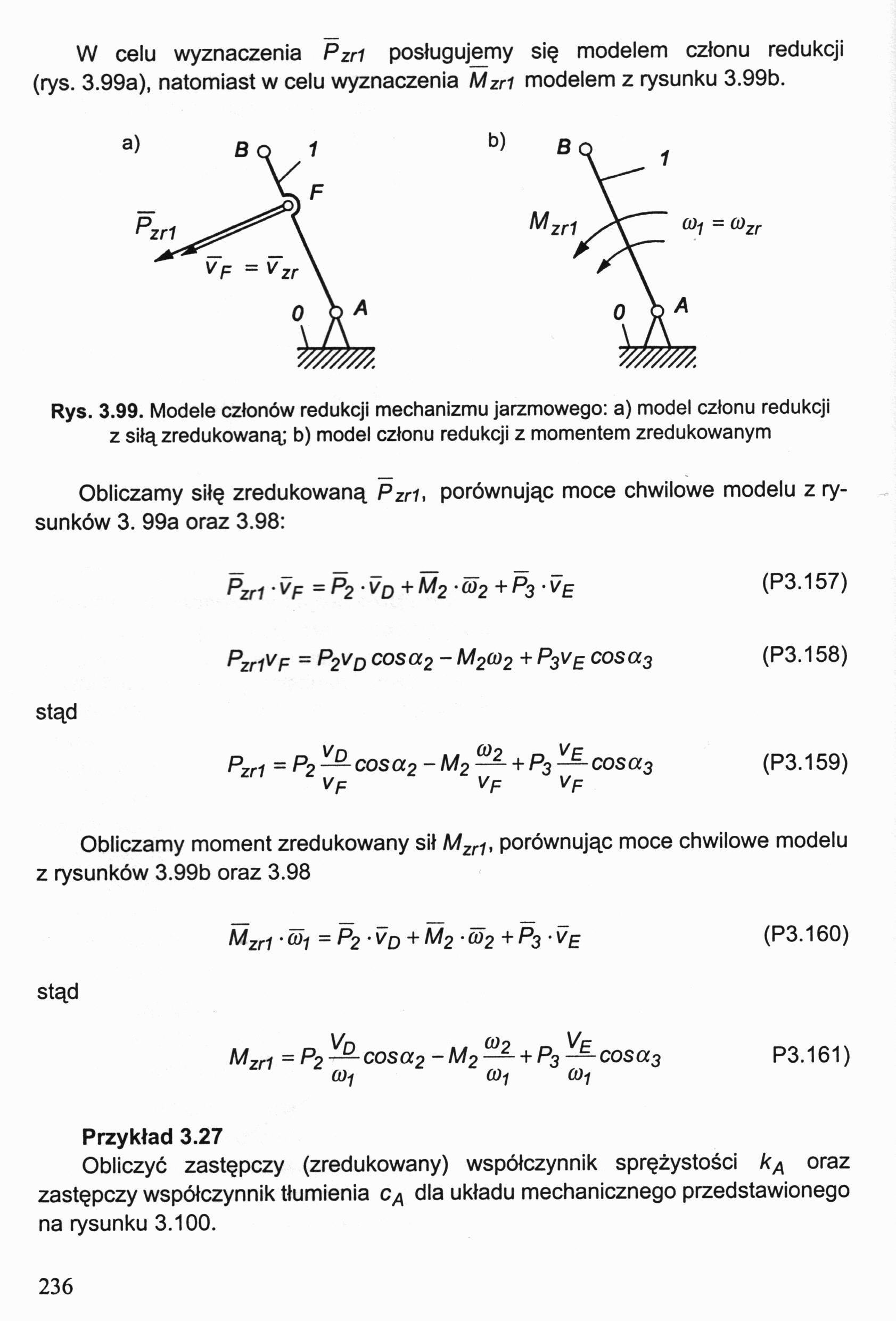
W celu wyznaczenia P_zri posługujemy się modelem członu redukcji (rys. 3.99a), natomiast w celu wyznaczenia Mzri modelem z rysunku 3.99b.

Rys. 3.99. Modele członów redukcji mechanizmu jarzmowego: a) model członu redukcji z siłą zredukowaną; b) model członu redukcji z momentem zredukowanym

Obliczamy siłę zredukowaną P_zri, porównując moce chwilowe modelu z rysunków 3. 99a oraz 3.98:

(P3.157)

Pzr 1 ^VF - Pz ^VD ⁺ ^2 '^u>2 + P3 ’^VE

P_zri^vF = P2^VD cosa₂ - M₂a>₂ + P₃V_E cosa₃    (P3.158)

stąd

^VF

co₂

^VF

^VF

P_zri = P₂ — cosa₂ - M₂ — + P₃ — cosa₃

(P3.159)

Obliczamy moment zredukowany sił M_zr1, porównując moce chwilowe modelu z rysunków 3.99b oraz 3.98

M_zri • (1)■) — P₂ • vq + M₂ • co₂ + P₃ ■ v_E    (P3.160)

stąd

Mzri ~ P2 — cosa₂ -M₂~ + P₃~cosa₃    P3.161)

U>1    U>1    CO-/

Przykład 3.27

Obliczyć zastępczy (zredukowany) współczynnik sprężystości k_A oraz zastępczy współczynnik tłumienia c_A dla układu mechanicznego przedstawionego na rysunku 3.100.

236