24 luty 07 (60)

Należy wyznaczyć masy korekcyjne m_k1, m_k2 oraz ich położenie cp_k1, ę_k2 tak, aby wyrównoważyć dynamicznie wał z zadanymi masami. Promienie korekcji wynoszą: r_k1 = 20 mm, r_k2 = 40 mm.

Rozwiązanie

Przyjmujemy położenie mas korekcyjnych zgodnie z rysunkiem 3.83.

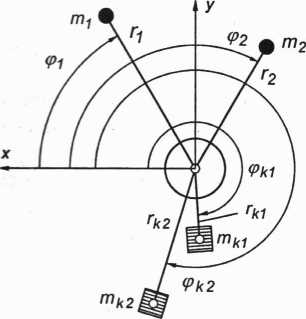
Rys. 3.83. Rozmieszczenie mas korekcyjnych

Warunki wyrównoważenia dynamicznego układu mają postać: n

5) mjXj = m_k1r_ki cosę_k1 +    cosę-i + m₂r₂ cosę₂ + m_k2r_k2 cosę_k2 = 0

i=1 n

m,y₍- = m_k1r_k1 sinę_k1 + sinę-t + m₂r₂ sinę₂ + m_k2r_k2 sirup_k2 = 0

(P3.128)

n

'£_im_ix_jz_i = m₁r₁lcosę₁ +m₂r₂ ■ 21 cos<p₂ +m_k2r_k2 ■3lcoscp_k2 = 0 i=1 n

mjYjZj = m₁r₁l sinę₁ + m₂r₂ ■ 21 sinę₂ + m_k2r_k2 ■ 31 sinę_k2 = 0

i=i

Z trzeciego i czwartego równania (P3.128) mamy

(P3.129)

_ sirupi + 2m₂r₂ simp₂ = m-jr-f coscpt + 2m₂r₂ cosę₂

stąd (p_k2 = 286,82°.

210