24 luty 07 (18)

Ri R_kt^T oznaczają w przypadku występowania tarcia ruchowego reakcje całkowite, jakimi ciało k działa na ciało / odpowiednio w punktach A i B. Reakcje te odchylają się od normalnej do prowadnicy o kąt p_r w ten sposób, że siły tarcia Tfi i Tu mają zwroty przeciwne do prędkości v_/k, czyli prędkości suwaka / względem prowadnicy k.

Przykład 3.11

Wyznaczyć reakcje w punktach A i B oraz podać warunek równowagi granicznej dla członu spoczywającego na_podłożu chropowatym.

Dane: Siła ciężkości członu G₂ oraz współczynnik tarcia podłoża w punkcie podparcia A - pf₂- Tarcie w punkcie B pominąć.

Rozwiązanie przedstawiono na rysunku 3.46.

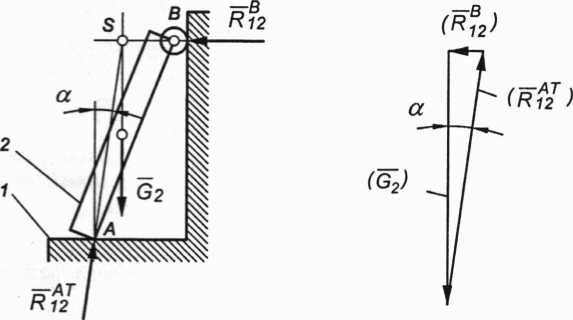
Rys. 3.46. Analiza układu sił działających na człon podparty na podłożu chropowatym

Uwzględniono tarcie w punkcie A. Równanie równowagi sił działających na człon 2 ma postać:

(P3.65)

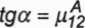
(P3.66)

Człon 2 pozostanie w równowadze dopóki a< p.

W parze kinematycznej postępowej z dociskiem dwustronnym występuje tzw. wspólna strefa tarcia.

Wspólna strefa tarcia (WST) jest to część wspólna przekrojów stożków tarcia, a zatem jest to obszar wyznaczony przez kierunki reakcji całkowitych, jakimi prowadnica oddziaływuje na suwak. WST wyznacza dopuszczalne kierunki działania siły zewnętrznej, przy której istnieje możliwość ruchu oraz kierunki, przy których ruch jest niemożliwy (występuje zjawisko samohamowności).

168