24 luty 07 (114)

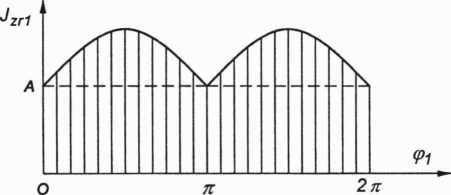
Rys. 3.115. Wykres zredukowanego momentu bezwładności mechanizmu jarzmowego J_zn((Pi)

Obliczenie zredukowanego momentu sił (rys. 3.116)

M_zri - (Pi = Ms -(pf + P3 - Vp    (P3.243)

M_zr1(Pt =M_s((>₁-P₃v_d    (P3.244)

M_zr1 =M_S- P₃l₁\sirup₁\ = a - bęi - PJ^sincp^ = M_czr1 - M_bzr1    (P3.245)

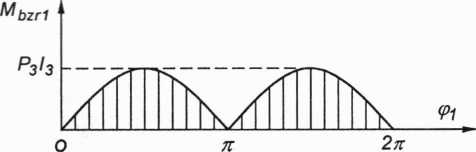
Rys. 3.116. Wykres zredukowanego momentu oporu mechanizmu jarzmowego M_bzr1(q>i) Równanie dynamiczne ruchu mechanizmu

M_zr,=J_2rt«i,₊^-4-    ^(P3'²⁴⁶⁾

dcpi 2

dJ

po podstawieniu: M_zr1; J_zr1, oraz pochodnej ^{u zr1} = m₃li sin 2(pf ostatecznie otrzy-

d(pi

mamy równanie ruchu mechanizmu w postaci

a-bę-j - P^lsincpi] = (m-,1+ J_S1 + m₂li + m₃l? sin² (p₁)(pi +

₁    (P3.247)

+ -m₃lf (sin2(p₁)(p²

Otrzymane równanie różniczkowe jest równaniem nieliniowym, jego rozwiązanie wymaga zastosowania metod numerycznych. W dalszej części podręcznika zostanie przedstawiona metoda rozwiązania równania tego typu.

264